ด้านสองด้านใดๆ ของสี่เหลี่ยมด้านขนานจะขนานกัน สี่เหลี่ยมด้านขนาน

สี่เหลี่ยมด้านขนานคือรูปสี่เหลี่ยมขนมเปียกปูนที่มีด้านตรงข้ามขนานกันเป็นคู่ (รูปที่ 233)

สำหรับรูปสี่เหลี่ยมด้านขนานตามอำเภอใจ จะมีคุณสมบัติต่อไปนี้:

1. ด้านตรงข้ามของสี่เหลี่ยมด้านขนานเท่ากัน

การพิสูจน์. ในสี่เหลี่ยมด้านขนาน ABCD เราวาดเส้นทแยงมุม AC สามเหลี่ยม ACD และ AC B เท่ากัน เนื่องจากมีด้าน AC ร่วมและมีมุมเท่ากันสองคู่อยู่ติดกัน:

(เช่น มุมขวางที่มีเส้นขนาน AD และ BC) ซึ่งหมายความว่า เช่นเดียวกับด้านของสามเหลี่ยมเท่ากันซึ่งอยู่ตรงข้ามกับมุมเท่ากัน ซึ่งเป็นสิ่งที่จำเป็นต้องพิสูจน์

2. มุมตรงข้ามของสี่เหลี่ยมด้านขนานเท่ากัน:

3. มุมที่อยู่ติดกันของสี่เหลี่ยมด้านขนาน เช่น มุมที่อยู่ติดกันด้านใดด้านหนึ่งบวกกัน เป็นต้น

การพิสูจน์คุณสมบัติ 2 และ 3 จะได้มาจากคุณสมบัติของมุมของเส้นขนานทันที

4. เส้นทแยงมุมของสี่เหลี่ยมด้านขนานจะตัดกันที่จุดตัดกัน กล่าวอีกนัยหนึ่ง

การพิสูจน์. สามเหลี่ยม AOD และ BOC เท่ากันทุกประการ เนื่องจากด้าน AD และ BC เท่ากัน (คุณสมบัติ 1) และมุมที่อยู่ติดกัน (เช่น มุมขวางของเส้นขนาน) จากตรงนี้ ด้านที่สอดคล้องกันของสามเหลี่ยมเหล่านี้จะเท่ากัน: AO ซึ่งเป็นสิ่งที่จำเป็นต้องพิสูจน์

คุณสมบัติทั้งสี่นี้แต่ละคุณสมบัติมีลักษณะเฉพาะของสี่เหลี่ยมด้านขนาน หรืออย่างที่พวกเขากล่าวกันว่าเป็นคุณสมบัติเฉพาะของมัน กล่าวคือ รูปสี่เหลี่ยมขนมเปียกปูนทุกอันที่มีคุณสมบัติเหล่านี้อย่างน้อยหนึ่งคุณสมบัติจะเป็นสี่เหลี่ยมด้านขนาน (และด้วยเหตุนี้ จึงมีคุณสมบัติทั้งสามที่เหลือทั้งหมด)

ให้เราดำเนินการพิสูจน์สำหรับแต่ละทรัพย์สินแยกกัน

1" ถ้าด้านตรงข้ามของรูปสี่เหลี่ยมขนมเปียกปูนเท่ากันเป็นคู่ๆ ก็จะเป็นรูปสี่เหลี่ยมด้านขนาน

การพิสูจน์. ให้รูปสี่เหลี่ยม ABCD มีด้าน AD และ BC, AB และ CD เท่ากันตามลำดับ (รูปที่ 233) ลองวาดเส้นทแยงมุม AC กัน สามเหลี่ยม ABC และ CDA จะเท่ากับมีสามคู่ ด้านที่เท่ากัน.

แต่มุม BAC กับ DCA จะเท่ากัน และ ความขนานกันของด้าน BC และ AD ตามมาจากความเท่ากันของมุม CAD และ ACB

2. ถ้ารูปสี่เหลี่ยมขนมเปียกปูนมีมุมตรงข้ามกันสองคู่เท่ากัน มันจะเป็นรูปสี่เหลี่ยมด้านขนาน

การพิสูจน์. อนุญาต . ตั้งแต่นั้นมาทั้งสองด้าน AD และ BC ขนานกัน (ขึ้นอยู่กับความขนานของเส้นตรง)

3. เราฝากสูตรและหลักฐานไว้กับผู้อ่าน

4. ถ้าเส้นทแยงมุมของรูปสี่เหลี่ยมตัดกันที่จุดตัด รูปสี่เหลี่ยมขนมเปียกปูนนั้นจะเป็นรูปสี่เหลี่ยมด้านขนาน

การพิสูจน์. ถ้า AO = OS, BO = OD (รูปที่ 233) สามเหลี่ยม AOD และ BOC จะเท่ากันราวกับว่ามี มุมเท่ากัน(แนวตั้ง!) ที่จุดยอด O ซึ่งอยู่ระหว่างคู่ที่มีด้านเท่ากัน AO และ CO, BO และ DO จากความเท่าเทียมกันของสามเหลี่ยม เราสรุปได้ว่าด้าน AD และ BC เท่ากัน ด้าน AB และ CD ก็เท่ากัน และรูปสี่เหลี่ยมขนมเปียกปูนกลายเป็นสี่เหลี่ยมด้านขนานตามคุณสมบัติเฉพาะ G

ดังนั้น เพื่อพิสูจน์ว่ารูปสี่เหลี่ยมขนมเปียกปูนที่กำหนดเป็นรูปสี่เหลี่ยมด้านขนาน ก็เพียงพอแล้วที่จะตรวจสอบความถูกต้องของคุณสมบัติใดๆ ในสี่คุณสมบัตินั้น ผู้อ่านได้รับเชิญให้พิสูจน์คุณสมบัติลักษณะอื่นของสี่เหลี่ยมด้านขนานอย่างอิสระ

5. ถ้ารูปสี่เหลี่ยมขนมเปียกปูนมีด้านคู่ขนานกันเท่ากัน รูปนั้นก็จะเป็นรูปสี่เหลี่ยมด้านขนาน

บางครั้งด้านขนานคู่ใดๆ ของสี่เหลี่ยมด้านขนานเรียกว่าฐาน ส่วนอีกสองด้านเรียกว่าด้านข้าง ส่วนของเส้นตรงที่ตั้งฉากกับด้านสองด้านของสี่เหลี่ยมด้านขนานที่ล้อมรอบระหว่างด้านนั้น เรียกว่า ความสูงของสี่เหลี่ยมด้านขนาน สี่เหลี่ยมด้านขนานในรูป 234 มีความสูง h ลากไปทางด้านข้าง AD และ BC ความสูงที่สองแสดงด้วยส่วน

แนวคิดเรื่องสี่เหลี่ยมด้านขนาน

คำจำกัดความ 1

สี่เหลี่ยมด้านขนานคือรูปสี่เหลี่ยมที่มีด้านตรงข้ามขนานกัน (รูปที่ 1)

รูปที่ 1.

สี่เหลี่ยมด้านขนานมีคุณสมบัติหลักสองประการ ลองพิจารณาโดยไม่มีข้อพิสูจน์

คุณสมบัติ 1: ด้านตรงข้ามและมุมของสี่เหลี่ยมด้านขนานจะเท่ากันตามลำดับ

คุณสมบัติ 2: เส้นทแยงมุมที่วาดในรูปสี่เหลี่ยมด้านขนานจะถูกแบ่งออกเป็นสองส่วนตามจุดตัด

สัญญาณของรูปสี่เหลี่ยมด้านขนาน

ลองพิจารณาคุณลักษณะสามประการของสี่เหลี่ยมด้านขนานแล้วนำเสนอในรูปแบบของทฤษฎีบท

ทฤษฎีบท 1

หากด้านสองด้านของรูปสี่เหลี่ยมด้านขนานเท่ากันและขนานกัน รูปสี่เหลี่ยมด้านขนานนี้ก็จะเป็นรูปสี่เหลี่ยมด้านขนาน

การพิสูจน์.

ให้เราได้รับรูปสี่เหลี่ยมขนมเปียกปูน $ABCD$ โดยที่ $AB||CD$ และ $AB=CD$ ให้เราวาดเส้นทแยงมุม $AC$ ในนั้น (รูปที่ 2)

รูปที่ 2.

พิจารณาเส้นคู่ขนาน $AB$ และ $CD$ และเส้นตัดกัน $AC$ แล้ว

\[\มุม CAB=\มุม DCA\]

เหมือนมุมที่ไขว้กัน

ตามเกณฑ์ $I$ ของความเท่าเทียมกันของรูปสามเหลี่ยม

เนื่องจาก $AC$ เป็นด้านร่วม และ $AB=CD$ ตามเงื่อนไข วิธี

\[\มุม DAC=\มุม ACB\]

พิจารณาเส้นตรง $AD$ และ $CB$ และเส้นตัดขวาง $AC$; จากความเท่ากันสุดท้ายของมุมนอน เราจะได้ $AD||CB$.) ดังนั้น ตามคำจำกัดความ $1$ รูปสี่เหลี่ยมขนมเปียกปูนนี้จึงเป็นสี่เหลี่ยมด้านขนาน

ทฤษฎีบทได้รับการพิสูจน์แล้ว

ทฤษฎีบท 2

ถ้าด้านตรงข้ามของรูปสี่เหลี่ยมขนมเปียกปูนเท่ากัน แสดงว่าเป็นรูปสี่เหลี่ยมด้านขนาน

การพิสูจน์.

ให้เราได้รับรูปสี่เหลี่ยมขนมเปียกปูน $ABCD$ โดยที่ $AD=BC$ และ $AB=CD$ ให้เราวาดเส้นทแยงมุม $AC$ ไว้ข้างใน (รูปที่ 3)

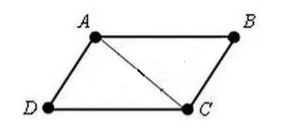
รูปที่ 3.

เนื่องจาก $AD=BC$, $AB=CD$ และ $AC$ เป็นด้านร่วม ดังนั้นตามเกณฑ์ $III$ สำหรับความเท่ากันของรูปสามเหลี่ยม

\[\สามเหลี่ยม DAC=\สามเหลี่ยม ACB\]

\[\มุม DAC=\มุม ACB\]

ลองพิจารณาเส้น $AD$ และ $CB$ และเส้นตัดขวาง $AC$; ดังนั้น ตามคำนิยาม $1$ รูปสี่เหลี่ยมด้านขนานนี้จึงเป็นสี่เหลี่ยมด้านขนาน

\[\มุม DCA=\มุม CAB\]

ให้เราพิจารณาเส้น $AB$ และ $CD$ และเส้นตัดขวาง $AC$; จากความเท่าเทียมกันสุดท้ายในมุมโกหก เราจะได้ $AB||CD$ ดังนั้น ตามคำจำกัดความที่ 1 รูปสี่เหลี่ยมขนมเปียกปูนนี้จึงเป็นสี่เหลี่ยมด้านขนาน

ทฤษฎีบทได้รับการพิสูจน์แล้ว

ทฤษฎีบท 3

หากเส้นทแยงมุมที่วาดเป็นรูปสี่เหลี่ยมขนมเปียกปูนถูกแบ่งออกเป็นสองส่วนเท่าๆ กันด้วยจุดตัดกัน รูปสี่เหลี่ยมด้านขนานนี้ก็จะเป็นรูปสี่เหลี่ยมด้านขนาน

การพิสูจน์.

ให้เราได้รับรูปสี่เหลี่ยมขนมเปียกปูน $ABCD$ ลองวาดเส้นทแยงมุม $AC$ และ $BD$ ลงไป ปล่อยให้พวกมันตัดกันที่จุด $O$ (รูปที่ 4)

รูปที่ 4.

เนื่องจากตามเงื่อนไข $BO=OD,\ AO=OC$ และมุม $\angle COB=\angle DOA$ นั้นเป็นแนวตั้ง ดังนั้น ด้วยเกณฑ์ $I$ สำหรับความเท่าเทียมกันของรูปสามเหลี่ยม

\[\สามเหลี่ยม BOC=\สามเหลี่ยม AOD\]

\[\มุม DBC=\มุม BDA\]

พิจารณาเส้น $BC$ และ $AD$ และเส้นตัดขวาง $BD$; โดยความเสมอภาคสุดท้ายข้ามมุมโกหก เราจะได้ $BC||AD$ $BC=AD$ เช่นกัน ดังนั้น ตามทฤษฎีบท $1$ รูปสี่เหลี่ยมขนมเปียกปูนนี้จึงเป็นสี่เหลี่ยมด้านขนาน

เช่นเดียวกับในเรขาคณิตแบบยุคลิด จุดและเส้นตรงเป็นองค์ประกอบหลักของทฤษฎีระนาบ ดังนั้น สี่เหลี่ยมด้านขนานจึงเป็นหนึ่งในตัวเลขสำคัญของรูปสี่เหลี่ยมขนมเปียกปูนนูน จากนั้นแนวคิดของ "สี่เหลี่ยมผืนผ้า" "สี่เหลี่ยมจัตุรัส" "สี่เหลี่ยมขนมเปียกปูน" และปริมาณทางเรขาคณิตอื่น ๆ ก็เหมือนกับเส้นด้ายจากลูกบอล

ความหมายของสี่เหลี่ยมด้านขนาน

รูปสี่เหลี่ยมนูน,ประกอบด้วยส่วนของเส้นตรง ซึ่งแต่ละคู่ขนานกัน ในทางเรขาคณิตเรียกว่าสี่เหลี่ยมด้านขนาน

ลักษณะของรูปสี่เหลี่ยมด้านขนานแบบคลาสสิกนั้นแสดงด้วยรูปสี่เหลี่ยม ABCD ด้านข้างเรียกว่าฐาน (AB, BC, CD และ AD) เส้นตั้งฉากที่ลากจากจุดยอดใดๆ ไปยังด้านที่อยู่ตรงข้ามกับจุดยอดนี้เรียกว่าความสูง (BE และ BF) เส้น AC และ BD เรียกว่าเส้นทแยงมุม

ความสนใจ!สี่เหลี่ยมจัตุรัส สี่เหลี่ยมขนมเปียกปูน และสี่เหลี่ยมผืนผ้าเป็นกรณีพิเศษของสี่เหลี่ยมด้านขนาน

ด้านและมุม: ลักษณะของความสัมพันธ์

คุณสมบัติที่สำคัญโดยส่วนใหญ่แล้ว กำหนดไว้ล่วงหน้าโดยการกำหนดนั้นเองพวกมันพิสูจน์ได้ด้วยทฤษฎีบท ลักษณะเหล่านี้มีดังนี้:

1. ด้านที่อยู่ตรงข้ามกันเป็นคู่เหมือนกัน
2. มุมที่อยู่ตรงข้ามกันจะเท่ากันเป็นคู่

พิสูจน์: พิจารณา ∆ABC และ ∆ADC ซึ่งได้มาจากการหาร ABCD ของรูปสี่เหลี่ยมขนมเปียกปูนด้วยเส้นตรง AC ∠BCA=∠CAD และ ∠BAC=∠ACD เนื่องจาก AC เป็นเรื่องธรรมดาสำหรับพวกมัน (มุมแนวตั้งสำหรับ BC||AD และ AB||CD ตามลำดับ) จากนี้ไป: ∆ABC = ∆ADC (เครื่องหมายที่สองของความเท่าเทียมกันของรูปสามเหลี่ยม)

ส่วน AB และ BC ใน ∆ABC สอดคล้องกันเป็นคู่กับเส้น CD และ AD ใน ∆ADC ซึ่งหมายความว่าทั้งสองเหมือนกัน: AB = CD, BC = AD ดังนั้น ∠B จึงสอดคล้องกับ ∠D และมีค่าเท่ากัน เนื่องจาก ∠A=∠BAC+∠CAD, ∠C=∠BCA+∠ACD ซึ่งเหมือนกันแบบคู่ ดังนั้น ∠A = ∠C คุณสมบัติได้รับการพิสูจน์แล้ว

ลักษณะของเส้นทแยงมุมของรูป

คุณสมบัติหลักของเส้นเหล่านี้ของสี่เหลี่ยมด้านขนาน: จุดตัดแบ่งครึ่ง

พิสูจน์: ให้นั่นคือเป็นจุดตัดของเส้นทแยงมุม AC และ BD ของรูป ABCD พวกมันสร้างรูปสามเหลี่ยมสมส่วนสองรูป - ∆ABE และ ∆CDE

AB=CD เนื่องจากตรงกันข้าม ตามเส้นและเซแคนต์ ∠ABE = ∠CDE และ ∠BAE = ∠DCE

ตามเกณฑ์ที่สองของความเท่าเทียมกัน ∆ABE = ∆CDE ซึ่งหมายความว่าองค์ประกอบ ∆ABE และ ∆CDE: AE = CE, BE = DE และในขณะเดียวกัน พวกมันก็เป็นส่วนที่เป็นสัดส่วนของ AC และ BD คุณสมบัติได้รับการพิสูจน์แล้ว

คุณสมบัติของมุมที่อยู่ติดกัน

ด้านที่อยู่ติดกันมีผลรวมของมุมเท่ากับ 180°เนื่องจากพวกมันอยู่บนด้านเดียวกันของเส้นขนานและแนวขวาง สำหรับรูปสี่เหลี่ยม ABCD:

∠A+∠B=∠C+∠D=∠A+∠D=∠B+∠C=180°

คุณสมบัติของเส้นแบ่งครึ่ง:

1. ลดลงไปด้านใดด้านหนึ่งตั้งฉาก
2. จุดยอดตรงข้ามมีเส้นแบ่งครึ่งขนาน
3. สามเหลี่ยมที่ได้จากการวาดเส้นแบ่งครึ่งจะเป็นหน้าจั่ว

การหาคุณลักษณะเฉพาะของสี่เหลี่ยมด้านขนานโดยใช้ทฤษฎีบท

คุณลักษณะของรูปนี้เป็นไปตามทฤษฎีบทหลักซึ่งระบุดังต่อไปนี้: รูปสี่เหลี่ยมขนมเปียกปูนถือเป็นรูปสี่เหลี่ยมด้านขนานในกรณีที่เส้นทแยงมุมตัดกัน และจุดนี้แบ่งพวกมันออกเป็นส่วนเท่าๆ กัน

พิสูจน์: ให้เส้น AC และ BD ของรูปสี่เหลี่ยม ABCD ตัดกันใน i.e. เนื่องจาก ∠AED = ∠BEC และ AE+CE=AC BE+DE=BD ดังนั้น ∆AED = ∆BEC (ขึ้นอยู่กับเกณฑ์แรกสำหรับความเท่าเทียมกันของรูปสามเหลี่ยม) นั่นคือ ∠EAD = ∠ECB นอกจากนี้ยังเป็นมุมตัดภายในของเส้นตัดขวาง AC สำหรับเส้น AD และ BC ดังนั้นตามคำจำกัดความของความเท่าเทียม - AD || บี.ซี. คุณสมบัติที่คล้ายกันของเส้น BC และ CD ก็ได้รับมาเช่นกัน ทฤษฎีบทได้รับการพิสูจน์แล้ว

การคำนวณพื้นที่ของรูป

พื้นที่ของรูปนี้ พบได้หลายวิธีวิธีที่ง่ายที่สุดวิธีหนึ่ง: การคูณความสูงและฐานที่วาด

พิสูจน์: ลากเส้นตั้งฉาก BE และ CF จากจุดยอด B และ C ∆ABE และ ∆DCF เท่ากัน เนื่องจาก AB = CD และ BE = CF ABCD มีขนาดเท่ากับสี่เหลี่ยม EBCF เนื่องจากประกอบด้วยตัวเลขที่เท่ากัน: S ABE และ S EBCD เช่นเดียวกับ S DCF และ S EBCD สืบเนื่องจากบริเวณนี้นั่นเอง รูปทรงเรขาคณิตตั้งอยู่ในลักษณะเดียวกับรูปสี่เหลี่ยมผืนผ้า:

S ABCD = S EBCF = BE×BC=BE×AD

ในการกำหนดสูตรทั่วไปสำหรับพื้นที่ของสี่เหลี่ยมด้านขนานเราจะแสดงความสูงเป็น HBและด้านข้าง - ข- ตามลำดับ:

วิธีอื่นในการค้นหาพื้นที่

การคำนวณพื้นที่ ผ่านด้านข้างของสี่เหลี่ยมด้านขนานและมุมซึ่งก่อตัวเป็นวิธีการที่สองที่รู้จัก

,

Spr-ma - พื้นที่;

a และ b เป็นด้านของมัน

α คือมุมระหว่างส่วน a และ b

วิธีการนี้ใช้ได้ผลจริงจากวิธีแรก แต่ในกรณีที่ไม่ทราบ จะตัดสามเหลี่ยมมุมฉากที่พบพารามิเตอร์ออกเสมอ อัตลักษณ์ตรีโกณมิตินั่นคือ เมื่อเปลี่ยนความสัมพันธ์ เราก็จะได้ ในสมการของวิธีแรก เราจะแทนที่ความสูงด้วยผลคูณนี้และรับหลักฐานยืนยันความถูกต้องของสูตรนี้

ผ่านเส้นทแยงมุมของสี่เหลี่ยมด้านขนานและมุมซึ่งพวกมันสร้างขึ้นเมื่อพวกมันตัดกัน คุณยังสามารถหาพื้นที่ได้อีกด้วย

พิสูจน์: AC และ BD ตัดกันเป็นรูปสามเหลี่ยมสี่รูป: ABE, BEC, CDE และ AED ผลรวมของพวกเขาเท่ากับพื้นที่ของรูปสี่เหลี่ยมนี้

พื้นที่ของแต่ละ ∆ สามารถพบได้โดยนิพจน์ โดยที่ a=BE, b=AE, ∠γ =∠AEB เนื่องจาก การคำนวณใช้ค่าไซน์เดียว นั่นก็คือ เนื่องจาก AE+CE=AC= d 1 และ BE+DE=BD= d 2 สูตรพื้นที่จึงลดลงเป็น:

.

การประยุกต์ในพีชคณิตเวกเตอร์

คุณลักษณะของส่วนประกอบที่เป็นส่วนประกอบของรูปสี่เหลี่ยมขนมเปียกปูนนี้พบการประยุกต์ใช้ในพีชคณิตเวกเตอร์ ซึ่งก็คือการบวกเวกเตอร์สองตัว กฎสี่เหลี่ยมด้านขนานระบุไว้ว่า ถ้าให้เวกเตอร์มาและไม่เป็นเส้นตรง จากนั้นผลรวมจะเท่ากับเส้นทแยงมุมของรูปนี้ ซึ่งฐานตรงกับเวกเตอร์เหล่านี้

พิสูจน์: จากจุดเริ่มต้นที่เลือกโดยพลการ - เช่น - สร้างเวกเตอร์และ . ต่อไป เราสร้างสี่เหลี่ยมด้านขนาน OASV โดยที่ส่วนของ OA และ OB อยู่ด้านข้าง ดังนั้นระบบปฏิบัติการจึงอยู่บนเวกเตอร์หรือผลรวม

สูตรคำนวณพารามิเตอร์ของสี่เหลี่ยมด้านขนาน

ข้อมูลระบุตัวตนจะได้รับภายใต้เงื่อนไขต่อไปนี้:

1. a และ b, α - ด้านและมุมระหว่างพวกเขา;
2. d 1 และ d 2, γ - เส้นทแยงมุมและ ณ จุดตัดกัน
3. h a และ h b - ความสูงลดลงไปทางด้าน a และ b;

พารามิเตอร์	สูตร
การหาด้านข้าง
ตามเส้นทแยงมุมและโคไซน์ของมุมระหว่างพวกมัน
ตามเส้นทแยงมุมและด้านข้าง
ผ่านความสูงและจุดยอดตรงข้าม
การหาความยาวของเส้นทแยงมุม
ที่ด้านข้างและขนาดของยอดระหว่างพวกเขา

ซิกกี ปา-รัล-เล-โล-แกรม-มา

1. ความหมายและคุณสมบัติพื้นฐานของรูปสี่เหลี่ยมด้านขนาน

เริ่มต้นด้วยการนึกถึงคำจำกัดความของ para-ral-le-lo-gram

คำนิยาม. สี่เหลี่ยมด้านขนาน- what-you-rekh-gon-nick ซึ่งมีด้าน pro-ti-false ทุก ๆ สองด้านที่ขนานกัน (ดูรูปที่ 1)

ข้าว. 1. ปา-ราล-เลอ-โล-แกรม

มาจำกัน คุณสมบัติพื้นฐานของพา-ราล-เลอ-โล-แกรม-มา:

เพื่อให้สามารถใช้คุณสมบัติเหล่านี้ได้ทั้งหมด คุณต้องแน่ใจว่า fi-gu-ra เกี่ยวกับใครบางคน -Roy เรากำลังพูดถึง, - พาราล-เลอ-โล-แกรม ในการทำเช่นนี้จำเป็นต้องรู้ข้อเท็จจริงเช่นสัญญาณของ pa-ral-le-lo-gram-ma เรากำลังดูสองคนแรกตอนนี้

2. เครื่องหมายแรกของรูปสี่เหลี่ยมด้านขนาน

ทฤษฎีบท. สัญญาณแรกของ pa-ral-le-lo-gram-maถ้าในถ่านหินสี่ก้อน ด้านตรงข้ามทั้งสองเท่ากันและขนานกัน ดังนั้นชื่อเล่นถ่านหินสี่ก้อนนี้ - สี่เหลี่ยมด้านขนาน. .

ข้าว. 2. สัญญาณแรกของ pa-ral-le-lo-gram-ma

การพิสูจน์. เราใส่ dia-go-nal ลงใน four-reh-coal-ni-ke (ดูรูปที่ 2) เธอแบ่งออกเป็น tri-coal-ni-ka สองอัน ลองเขียนสิ่งที่เรารู้เกี่ยวกับสามเหลี่ยมเหล่านี้:

ตามเครื่องหมายแรกของความเท่าเทียมกันของรูปสามเหลี่ยม

จากความเท่าเทียมกันของสามเหลี่ยมที่ระบุตามมาด้วยสัญลักษณ์ของความขนานของเส้นตรงเมื่อข้าม ch-nii s-ku-shchi ของพวกเขา เรามีสิ่งนั้น:

โด-คา-ซ่า-แต่

3. เครื่องหมายที่สองของสี่เหลี่ยมด้านขนาน

ทฤษฎีบท. เครื่องหมายที่สองคือ pa-ral-le-lo-gram-maถ้าในสี่มุมทุกสองด้านตรงข้ามเท่ากัน แล้วสี่มุมนี้ก็เท่ากับ สี่เหลี่ยมด้านขนาน. .

ข้าว. 3. สัญลักษณ์ที่สองของ pa-ral-le-lo-gram-ma

การพิสูจน์. เราใส่ไดอะโกนัลไว้ที่มุมทั้งสี่ (ดูรูปที่ 3) เธอแบ่งมันออกเป็นสามเหลี่ยมสองอัน ลองเขียนสิ่งที่เรารู้เกี่ยวกับสามเหลี่ยมเหล่านี้ตามรูปแบบของทฤษฎี:

ตามเครื่องหมายที่สามของความเท่าเทียมกันของรูปสามเหลี่ยม

จากความเท่าเทียมกันของรูปสามเหลี่ยม ตามมาด้วยเครื่องหมายของเส้นคู่ขนาน เมื่อพวกมันตัดกัน s-ku-shchey มากินกันเถอะ:

พาร์-ราล-เลอ-โล-แกรม ตามคำนิยาม Q.E.D.

โด-คา-ซ่า-แต่

4. ตัวอย่างการใช้คุณลักษณะสี่เหลี่ยมด้านขนานแรก

ลองดูตัวอย่างการใช้สัญลักษณ์ของ pa-ral-le-lo-gram

ตัวอย่างที่ 1. ในส่วนที่นูนไม่มีถ่านหิน ค้นหา: ก) มุมของถ่านหิน; b) ร้อยรูดี

สารละลาย. ภาพประกอบ รูปที่. 4.

pa-ral-le-lo-gram ตามสัญญาณแรกของ pa-ral-le-lo-gram-ma

ก. โดยสมบัติของพาร์-ราล-เลอ-โล-แกรมเกี่ยวกับมุมโปร-ติ-เท็จ โดยสมบัติของพาร์-ราล-เลอ-โล-แกรมเกี่ยวกับผลรวมของมุม เมื่อนอนตะแคงข้างหนึ่ง

บี. โดยธรรมชาติของความเสมอภาคของฝ่ายสนับสนุนเท็จ

เครื่องหมายซ้ำ pa-ral-le-lo-gram-ma

5. ทบทวน: ความหมายและคุณสมบัติของสี่เหลี่ยมด้านขนาน

จำไว้ว่า สี่เหลี่ยมด้านขนาน- นี่คือมุมสี่เหลี่ยมจัตุรัสซึ่งมีด้านโปรติเท็จเป็นคู่ นั่นคือถ้า - par-ral-le-lo-gram แล้ว (ดูรูปที่ 1)

Parallel-le-lo-gram มีคุณสมบัติหลายประการ: มุมตรงข้ามเท่ากัน () มุมตรงข้าม -เราเท่ากัน ( - นอกจากนี้ เดีย-โก-นา-ลี ปา-ราล-เล-โล-แกรม-มา ณ จุดเร-เซ-เช-นิยะ จะถูกแบ่งออกตามผลรวมของมุม โดยที่-เล- กดไปทางใดๆ ด้าน pa-ral-le-lo-gram-ma เท่ากับ ฯลฯ

แต่เพื่อที่จะใช้ประโยชน์จากคุณสมบัติเหล่านี้ทั้งหมด จำเป็นต้องแน่ใจอย่างแน่นอนว่า ri-va-e-my th-you-rekh-coal-nick - pa-ral-le-lo-gram เพื่อจุดประสงค์นี้ มีสัญญาณของ par-ral-le-lo-gram: นั่นคือข้อเท็จจริงเหล่านั้นซึ่งสามารถสรุปได้เพียงคุณค่าเดียว ว่าสิ่งที่คุณ rekh-coal-nick เป็น par-ral- เลอ-โล-แกรม-แม่ ในบทเรียนที่แล้ว เราได้ดูสัญญาณสองประการแล้ว ตอนนี้เรากำลังดูครั้งที่สาม

6. เครื่องหมายที่สามของสี่เหลี่ยมด้านขนานและการพิสูจน์

หากในถ่านหินสี่ก้อนมีไดอาโกออน ณ จุดรีเซเชนิยะที่พวกเขาทำบายลัม ดังนั้นโรห์โคลนิคที่คุณให้สี่คนนั้นเป็นปาราเล -โล-แกรม-แม่.

ที่ให้ไว้:

สิ่งที่คุณเป็นถ่านหินนิค; - -

พิสูจน์:

สี่เหลี่ยมด้านขนาน.

การพิสูจน์:

เพื่อที่จะพิสูจน์ข้อเท็จจริงนี้ จำเป็นต้องแสดงความเท่าเทียมของคู่สัญญากับพาร์-เลอ-โล-แกรม และความขนานของเส้นตรงส่วนใหญ่มักปรากฏผ่านความเท่าเทียมกันของมุมขวางภายในที่มุมขวาเหล่านี้ ดังนั้น นี่คือวิธีถัดไปในการรับเครื่องหมายที่สามของพาร์-ราล -เลอ-โล-แกรม-มา: ผ่านความเท่าเทียมกันของรูปสามเหลี่ยม .

ลองดูว่าสามเหลี่ยมเหล่านี้เท่ากันอย่างไร แท้จริงแล้วจากเงื่อนไขดังต่อไปนี้: . นอกจากนี้ เนื่องจากมุมเป็นแนวตั้ง จึงมีเท่ากัน นั่นคือ:

(สัญญาณแรกของความเท่าเทียมกันไตรถ่านหิน-ni-cov- ตามสองด้านและมุมระหว่างพวกเขา)

จากความเท่าเทียมกันของรูปสามเหลี่ยม: (เนื่องจากมุมขวางภายในของเส้นตรงและหน้าตัดเหล่านี้เท่ากัน) นอกจากนี้ จากความเท่าเทียมกันของรูปสามเหลี่ยมจะเป็นไปตามนั้น . ซึ่งหมายความว่าเราเข้าใจว่าในสี่ถ่านหินสองร้อยมีค่าเท่ากันและขนานกัน ตามสัญญาณแรก pa-ral-le-lo-gram-ma: - pa-ral-le-lo-gram

โด-คา-ซ่า-แต่

7. ตัวอย่างปัญหาบนเครื่องหมายที่สามของสี่เหลี่ยมด้านขนานและลักษณะทั่วไป

ลองดูตัวอย่างการใช้เครื่องหมายที่สามของ pa-ral-le-lo-gram

ตัวอย่างที่ 1

ที่ให้ไว้:

- สี่เหลี่ยมด้านขนาน; - - se-re-di-na, - se-re-di-na, - se-re-di-na, - se-re-di-na (ดูรูปที่ 2)

พิสูจน์:- พา-ราล-เลอ-โล-แกรม

การพิสูจน์:

ซึ่งหมายความว่าในสี่ถ่านหิน-โน-เดีย-โก-ออน-ไม่ว่าพวกเขาจะทำบายลัม ณ จุดเรเซเชนิยะหรือไม่ก็ตาม. ด้วยเครื่องหมายที่สามของ pa-ral-le-lo-gram ตามมาจากนี้ - pa-ral-le-lo-gram

โด-คา-ซ่า-แต่

หากคุณวิเคราะห์เครื่องหมายที่สามของ pa-ral-le-lo-gram คุณจะสังเกตได้ว่าเครื่องหมายนี้ตรงกับสัตวแพทย์- มีคุณสมบัติเป็น par-ral-le-lo-gram นั่นคือความจริงที่ว่า เดีย-โก-นา-ลี เด-ลา-เซียไม่ได้เป็นเพียงคุณสมบัติของพาร์-เล-โล-แกรมเท่านั้น แต่ยังมีความโดดเด่นคือ คา-รัก-เต-รี-สติ-เช- ทรัพย์สินซึ่งสามารถแยกแยะได้จากชุด what-you-rekh-coal-ni-cov

แหล่งที่มา

http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/priznaki-parallelogramma

http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/tretiy-priznak-parallelogramma

http://www.uchportfolio.ru/users_content/675f9820626f5bc0afb47b57890b466e/images/46TThxQ8j4Y.jpg

http://cs10002.vk.me/u31195134/116260458/x_56d40dd3.jpg

http://wwww.tepka.ru/geometriya/16.1.gif

สี่เหลี่ยมด้านขนานคือรูปสี่เหลี่ยมขนมเปียกปูนที่มีด้านตรงข้ามขนานกันเป็นคู่ รูปต่อไปนี้แสดงรูปสี่เหลี่ยมด้านขนาน ABCD มีด้าน AB ขนานกับด้าน CD และด้าน BC ขนานกับด้าน AD

ดังที่คุณคงเดาได้ สี่เหลี่ยมด้านขนานเป็นรูปสี่เหลี่ยมขนมเปียกปูนนูน ลองพิจารณาคุณสมบัติพื้นฐานของรูปสี่เหลี่ยมด้านขนานกัน

คุณสมบัติของสี่เหลี่ยมด้านขนาน

1. ในสี่เหลี่ยมด้านขนาน มุมตรงข้ามและด้านตรงข้ามจะเท่ากัน มาพิสูจน์คุณสมบัตินี้กัน - พิจารณาสี่เหลี่ยมด้านขนานที่แสดงในรูปต่อไปนี้

เส้นทแยงมุม BD แบ่งออกเป็นสองส่วน สามเหลี่ยมเท่ากัน: ABD และ CBD พวกมันจะเท่ากันตลอดด้าน BD และมุมสองมุมที่อยู่ติดกัน เนื่องจากมุมที่วางขวางที่เส้นตัด BD ของเส้นคู่ขนาน BC และ AD และ AB และ CD ตามลำดับ ดังนั้น AB = ซีดี และ
พ.ศ. = ค.ศ. และจากความเท่าเทียมกันของมุม 1, 2, 3 และ 4 จะได้ว่ามุม A = มุม 1 + มุม 3 = มุม 2 + มุม 4 = มุม C

2. เส้นทแยงมุมของสี่เหลี่ยมด้านขนานจะถูกแบ่งครึ่งตามจุดตัด ให้จุด O เป็นจุดตัดของเส้นทแยงมุม AC และ BD ของสี่เหลี่ยมด้านขนาน ABCD

จากนั้นสามเหลี่ยม AOB และสามเหลี่ยม COD จะเท่ากัน ตามแนวด้านข้างและมุมสองมุมที่อยู่ติดกัน (AB = CD เนื่องจากสิ่งเหล่านี้เป็นด้านตรงข้ามของสี่เหลี่ยมด้านขนาน และ angle1 = angle2 และ angle3 = angle4 เป็นมุมขวาง เมื่อเส้น AB และ CD ตัดกับเซแคนต์ AC และ BD ตามลำดับ) จากนี้ จะได้ว่า AO = OC และ OB = OD ซึ่งจำเป็นต้องพิสูจน์

คุณสมบัติหลักทั้งหมดแสดงไว้ในสามรูปต่อไปนี้