अनुसंधान परियोजना "चेकर्ड पेपर की ज्यामिति में पीक फॉर्मूला। स्कूल प्लानिमेट्री कोर्स में पीक फॉर्मूला
काम का पाठ छवियों और सूत्रों के बिना रखा गया है।
कार्य का पूर्ण संस्करण "कार्य फ़ाइलें" टैब में PDF स्वरूप में उपलब्ध है
परिचय
मैं छठी कक्षा का छात्र हूं। मैंने पिछले साल से ज्यामिति का अध्ययन करना शुरू किया, क्योंकि मैं पाठ्यपुस्तक "गणित" के अनुसार स्कूल में पढ़ता हूं। अंकगणित। ज्यामिति "Y.A. द्वारा संपादित। बनिमोविच, एल.वी. कुज़नेत्सोवा, एस.एस. मिनेवा और अन्य।
मेरा अधिकांश ध्यान "आंकड़ों के वर्ग", "सूत्र तैयार करना" विषयों पर आकर्षित हुआ। मैंने देखा कि एक ही आकार के क्षेत्रों को अलग-अलग तरीकों से पाया जा सकता है। रोजमर्रा की जिंदगी में, हमें अक्सर एक क्षेत्र खोजने के कार्यों का सामना करना पड़ता है। उदाहरण के लिए, पेंट किए जाने वाले फर्श का क्षेत्रफल ज्ञात कीजिए। यह उत्सुक है, आखिरकार, नवीनीकरण के लिए आवश्यक मात्रा में वॉलपेपर खरीदने के लिए, आपको कमरे के आकार को जानने की जरूरत है, अर्थात। दीवार क्षेत्र। एक वर्ग, आयत और समकोण त्रिभुज के क्षेत्रफल की गणना करना मेरे लिए सरल था।
इस विषय में दिलचस्पी लेने के बाद, मैंने इंटरनेट पर अतिरिक्त सामग्री की तलाश शुरू कर दी। अपनी खोजों के परिणामस्वरूप, मुझे पिक का सूत्र मिला - यह चेकर पेपर पर खींचे गए बहुभुज के क्षेत्र की गणना करने का एक सूत्र है। इस सूत्र का उपयोग करके क्षेत्र की गणना करना मुझे किसी भी छात्र के लिए सुलभ प्रतीत होता है। इसलिए मैंने शोध कार्य करने का निर्णय लिया।
विषय की प्रासंगिकता:
यह विषय ज्यामिति पाठ्यक्रम के अध्ययन का एक अतिरिक्त और गहनता है।
इस विषय का अध्ययन करने से आपको ओलंपियाड और परीक्षाओं की बेहतर तैयारी करने में मदद मिलेगी।
उद्देश्य:
पिक का फॉर्मूला देखें।
पिक फॉर्मूला का उपयोग करके ज्यामितीय समस्याओं को हल करने की तकनीकों में महारत हासिल करें।
सैद्धांतिक और व्यावहारिक सामग्री को व्यवस्थित और सारांशित करना।
अनुसंधान के उद्देश्य:
समस्याओं को हल करने में सूत्र का उपयोग करने की प्रभावशीलता और व्यवहार्यता की जाँच करें।
बदलती जटिलता की समस्याओं में पीक फॉर्मूला लागू करना सीखें।
पिक फॉर्मूला और पारंपरिक पद्धति का उपयोग करके हल की गई समस्याओं की तुलना करें।
मुख्य हिस्सा
1.1. इतिहास संदर्भ
जॉर्ज अलेक्जेंडर पिक एक ऑस्ट्रियाई गणितज्ञ हैं, जिनका जन्म 10 अगस्त, 1859 को हुआ था। वह एक प्रतिभाशाली बच्चा था, जिसे उसके पिता ने पढ़ाया था, जो एक निजी संस्थान का नेतृत्व करता था। 16 साल की उम्र में, जॉर्ज ने हाई स्कूल से स्नातक किया और वियना विश्वविद्यालय में प्रवेश किया। 20 साल की उम्र में उन्हें भौतिकी और गणित पढ़ाने का अधिकार मिला। बहुभुजों की एक जाली का क्षेत्रफल ज्ञात करने के सूत्र ने उन्हें विश्वव्यापी ख्याति दिलाई। उन्होंने 1899 में एक लेख में अपना सूत्र प्रकाशित किया। यह तब लोकप्रिय हुआ जब 1969 में पोलिश वैज्ञानिक ह्यूगो स्टीनहॉस ने गणितीय तस्वीरों के प्रकाशन में इसे शामिल किया।
जॉर्ज पिक ने वियना विश्वविद्यालय में शिक्षा प्राप्त की और 1880 में अपनी पीएचडी का बचाव किया। डॉक्टरेट की पढ़ाई पूरी करने के बाद, उन्हें प्राग में शेर्ल-फर्डिनेंड विश्वविद्यालय में अर्नेस्ट मच का सहायक नियुक्त किया गया। वे वहां शिक्षक भी बने। वह 1927 में अपनी सेवानिवृत्ति तक प्राग में रहे और फिर वियना लौट आए।
पिक ने प्राग के जर्मन विश्वविद्यालय में एक समिति की अध्यक्षता की, जिसने 1911 में गणितीय भौतिकी विभाग में आइंस्टीन के प्रोफेसर की नियुक्ति की।
उन्हें चेक एकेडमी ऑफ आर्ट्स एंड साइंसेज का सदस्य चुना गया था, लेकिन प्राग पर नाजी कब्जे के बाद उन्हें निष्कासित कर दिया गया था।
जब 12 मार्च, 1938 को नाजियों ने ऑस्ट्रिया में प्रवेश किया, तो वह प्राग लौट आया। मार्च 1939 में, नाजियों ने चेकोस्लोवाकिया पर आक्रमण किया। 13 जुलाई, 1942 को, पीक को उत्तरी बोहेमिया में नाजियों द्वारा स्थापित थेरेसिएन्स्टेड शिविर में भेज दिया गया, जहाँ दो सप्ताह बाद 82 वर्ष की आयु में उनकी मृत्यु हो गई।
1.2. अनुसंधान और प्रमाण
मैंने अपना शोध कार्य इस प्रश्न को स्पष्ट करके शुरू किया: मुझे किन आंकड़ों के क्षेत्र मिल सकते हैं? मैं विभिन्न त्रिभुजों और चतुर्भुजों के क्षेत्रफल की गणना के लिए एक सूत्र के साथ आ सकता हूं। लेकिन बहुभुज के साथ पांच, छह और सामान्य तौर पर क्या?
विभिन्न साइटों पर शोध के दौरान, मैंने पांच, छह और अन्य बहुभुजों के क्षेत्र की गणना के लिए समस्याओं के समाधान देखे। इन समस्याओं के समाधान के सूत्र को पिक सूत्र कहा जाता था। वह इस तरह दिखती है: S = बी + जी / 2-1, कहाँ पे वी- बहुभुज के अंदर स्थित नोड्स की संख्या, जी- बहुभुज की सीमा पर स्थित नोड्स की संख्या। इस सूत्र की ख़ासियत यह है कि इसका उपयोग केवल चेकर पेपर पर खींचे गए बहुभुजों के लिए किया जा सकता है।
ऐसे किसी भी बहुभुज को आसानी से त्रिभुजों में विभाजित किया जा सकता है जिसमें जाली के नोड्स पर शिखर होते हैं, जिसमें अंदर या किनारों पर नोड्स नहीं होते हैं। यह दिखाया जा सकता है कि इन सभी त्रिभुजों के क्षेत्रफल समान और ½ के बराबर हैं, और इसलिए, बहुभुज का क्षेत्रफल उनकी संख्या का आधा है टी।
इस संख्या को ज्ञात करने के लिए, हम बहुभुज की भुजाओं की संख्या को n से निरूपित करते हैं वी- इसके अंदर नोड्स की संख्या, के माध्यम से जी- कोने सहित पक्षों पर नोड्स की संख्या। सभी त्रिभुजों के कोणों का योग 180° होता है। टी।
आइए अब योग को एक अलग तरीके से खोजें।
किसी भी आंतरिक नोड पर शीर्ष के साथ कोणों का योग 2.180 ° है, अर्थात। कोणों का योग 360° होता है। वी;पक्षों पर नोड्स पर कोणों का कुल योग, लेकिन शीर्षों पर नहीं, है ( जी-एन) 180°, और बहुभुज के शीर्षों पर कोणों का योग होगा ( जी-2) 180°. इस तरह, टी = 2.180 डिग्री। बी + (जी-एन) 180° + (एन -2)180 °. कोष्ठक का विस्तार करने और 360 ° से विभाजित करने के बाद, हमें बहुभुज के क्षेत्र S के लिए एक सूत्र मिलता है, जिसे पिक सूत्र के रूप में जाना जाता है।
2. व्यावहारिक भाग
मैंने OGE-2017 संग्रह से कार्यों पर इस सूत्र की जाँच करने का निर्णय लिया। मैंने एक त्रिभुज, चतुर्भुज और पंचभुज के क्षेत्रफल की गणना करने के लिए कार्य लिया। मैंने उत्तरों की तुलना करने का निर्णय लिया, दो तरीकों से हल किया: 1) मैंने आयत में आंकड़े जोड़े और परिणामी आयत के क्षेत्र से मैंने समकोण त्रिभुजों का क्षेत्रफल घटाया; 2) लागू पिक का सूत्र।
एस = 18-1.5-4.5 = 12 और एस = 7 + 12 / 2-1 = 12
एस = 24-9-3 = 12 और एस = 7 + 12 / 2-1 = 12
एस = 77-7.5-12-4.5-4 = 49 और एस = 43 + 14 / 2-1 = 49
प्राप्त की तुलना करते हुए, मैं यह निष्कर्ष निकालता हूं कि दोनों सूत्र एक ही उत्तर देते हैं। पीक फॉर्मूला का उपयोग करके एक आकृति का क्षेत्रफल खोजना तेज़ और आसान हो गया, क्योंकि कम गणनाएँ थीं। समाधान में आसानी और गणना में समय की बचत भविष्य में OGE पास करते समय मेरे लिए उपयोगी होगी।
इसने मुझे अधिक जटिल आकृतियों पर पिक के सूत्र को लागू करने की संभावना का परीक्षण करने के लिए प्रेरित किया।
एस = 0 + 4/2 -1 = 1
एस = 5 + 11 / 2-1 = 9.5
एस = 4 + 16 / 2-1 = 1
निष्कर्ष
पीक का सूत्र समझने में आसान और उपयोग में आसान है। सबसे पहले, यह गिनने, 2 से विभाजित करने, जोड़ने और घटाने में सक्षम होने के लिए पर्याप्त है। दूसरे, आप बहुत समय खर्च किए बिना एक क्षेत्र और एक जटिल आकार पा सकते हैं। तीसरा, यह सूत्र किसी भी बहुभुज के लिए कार्य करता है।
नुकसान यह है कि पिक फॉर्मूला केवल उन आकृतियों के लिए लागू होता है जो चेकर पेपर पर खींची जाती हैं और कोने कोशिकाओं के नोड्स पर स्थित होते हैं।
मुझे विश्वास है कि अंतिम परीक्षा उत्तीर्ण करते समय अंकों के क्षेत्रफल की गणना करने में कोई कठिनाई नहीं आएगी। आखिरकार, मैं पिक के सूत्र से पहले से ही परिचित हूं।
ग्रन्थसूची
बनिमोविच ई.ए., डोरोफीव जी.वी., सुवोरोवा एस.बी. और अन्य गणित। अंकगणित। ज्यामिति। ग्रेड 5: शैक्षिक। सामान्य शिक्षा के लिए। adj के साथ संगठन इलेक्ट्रॉन को। कैरियर-तीसरा संस्करण। -एम।: शिक्षा, 2014.- 223, पी। : बीमार। - (गोले)।
बनिमोविच ई.ए., कुज़नेत्सोवा एल.वी., मिनेवा एस.एस. और अन्य गणित। अंकगणित। ज्यामिति। ग्रेड 6: शैक्षिक। सामान्य शिक्षा के लिए। संगठन-5वां संस्करण।-एम।: शिक्षा, 2016.-240। : बीमार। - (क्षेत्र)।
वासिलिव एन.बी. पिक के फार्मूले के आसपास। // मात्रा। - 1974.-№2। -एस 39-43
रसोलोव वी.वी. प्लानिमेट्री कार्य। / 5 वां संस्करण।, रेव। और जोड़। - एम।: 2006.-640 एस।
आई.वी. यशचेंको, ओजीई। गणित: विशिष्ट परीक्षा विकल्प: ओ -39 36 विकल्प - एम।: राष्ट्रीय शिक्षा प्रकाशन गृह, 2017. -240 पी। - (ओजीई। एफआईपीआई-स्कूल)।
"मैं ओजीई को हल करूंगा": गणित। दिमित्री गुशचिन की प्रशिक्षण प्रणाली। OGE-2017: कार्य, उत्तर, समाधान [इलेक्ट्रॉनिक संसाधन]। एक्सेस मोड: https://oge.sdamgia.ru/test?id=6846966 (उपचार की तिथि 04/02/2017)
पिक फॉर्मूला का उपयोग करके, आप एक सेल (त्रिकोण, वर्ग, समलम्बाकार, आयत, बहुभुज) में एक शीट पर बनी आकृति का क्षेत्रफल ज्ञात कर सकते हैं।
परीक्षा में होने वाले कार्यों में, कार्यों का एक पूरा समूह होता है जिसमें एक बहुभुज दिया जाता है, एक सेल में एक शीट पर बनाया जाता है और प्रश्न क्षेत्र खोजने के बारे में होता है। सेल का पैमाना एक वर्ग सेंटीमीटर है।
प्रस्तुति सामग्री देखें

जॉर्ज पीक
जॉर्ज अलेक्जेंडर पीक,
ऑस्ट्रियाई गणितज्ञ
(10.08.1859 - 13.07.1942)

सूत्र की खोज 1899 में हुई थी।
आवश्यक आकृति का क्षेत्रफल सूत्र द्वारा ज्ञात किया जा सकता है:
- एम त्रिभुज की सीमा पर (पक्षों और कोने पर) नोड्स की संख्या है:
- एन त्रिभुज के अंदर नोड्स की संख्या है;
* "नोड्स" से हमारा तात्पर्य रेखाओं के प्रतिच्छेदन से है।

आइए त्रिभुज का क्षेत्रफल ज्ञात करें:

आइए नोड्स को चिह्नित करें:
1 सेल = 1 सेमी
- एम = 15 (लाल रंग में चिह्नित)
- एन = 34 (नीले रंग में चिह्नित)

समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए:

आइए नोड्स को चिह्नित करें:
- एम = 18 (लाल रंग में चिह्नित)
- एन = 20 (नीले रंग में चिह्नित)

आइए समलम्ब चतुर्भुज का क्षेत्रफल ज्ञात करें:

आइए नोड्स को चिह्नित करें:
- एम = 24 (लाल रंग में चिह्नित)
- एन = 25 (नीले रंग में चिह्नित)

बहुभुज का क्षेत्रफल ज्ञात कीजिए:

आइए नोड्स को चिह्नित करें:
- एम = 14 (लाल रंग में चिह्नित)
- एन = 43 (नीले रंग में चिह्नित)



आइए नोड्स को चिह्नित करें:
- एम = 11 (लाल रंग में चिह्नित)
- एन = 5 (नीले रंग में चिह्नित)

अपने लिए तय करें:
1. 1 सेमी x 1 सेमी के सेल आकार के साथ चेकर पेपर पर दर्शाए गए चतुर्भुज का क्षेत्रफल ज्ञात करें। अपना उत्तर वर्ग सेंटीमीटर में दें।



4. 1 सेमी x 1 सेमी के सेल आकार वाले चेकर पेपर पर दर्शाए गए चतुर्भुज का क्षेत्रफल ज्ञात करें। अपना उत्तर वर्ग सेंटीमीटर में दें .


आइए इसके निकट एक आयत का वर्णन करें:
- आयत के क्षेत्र से (इस मामले में, यह एक वर्ग है), हम परिणामी सरल आंकड़ों के क्षेत्रों को घटाते हैं:


उत्तर:
№ कार्य
विकल्प 1
विकल्प 2
विकल्प 3
विकल्प 4

पीक फॉर्मूला
सज़िना वेलेरिया एंड्रीवाना, कक्षा 9 के छात्र, MAOU "माध्यमिक विद्यालय नंबर 11" उस्त-इलिम्स्क, इरकुत्स्क क्षेत्र
पर्यवेक्षक: गुबर ओक्साना मिखाइलोव्ना, उच्चतम योग्यता श्रेणी के गणित के शिक्षक MAOU "माध्यमिक विद्यालय नंबर 11" उस्त-इलिम्स्क, इरकुत्स्क क्षेत्र
2016 वर्ष
परिचय
ज्यामिति के विषय "बहुभुज के क्षेत्र" का अध्ययन करते समय, मैंने यह पता लगाने का निर्णय लिया: क्या उन क्षेत्रों से भिन्न क्षेत्रों को खोजने का कोई तरीका है जिनका हमने पाठों में अध्ययन किया था?
इस तरह पीक फॉर्मूला है। एल वी गोरिना ने "छात्रों की स्व-शिक्षा के लिए सामग्री" में इस सूत्र का वर्णन इस प्रकार किया है: "यूएसई और राज्य परीक्षा की पूर्व संध्या पर पिक के फॉर्मूले से परिचित होना विशेष रूप से महत्वपूर्ण है। इस सूत्र का उपयोग करके, आप परीक्षा में दी जाने वाली समस्याओं के एक बड़े वर्ग को आसानी से हल कर सकते हैं - ये चेकर पेपर पर दर्शाए गए बहुभुज के क्षेत्र को खोजने की समस्याएं हैं। पिक का छोटा सूत्र ऐसी समस्याओं को हल करने के लिए आवश्यक सूत्रों के पूरे सेट को बदल देगा। पिक का फॉर्मूला काम करेगा "वन फॉर ऑल..."!"।
परीक्षा की सामग्री में, मुझे भूमि भूखंडों का क्षेत्र खोजने पर व्यावहारिक सामग्री के साथ समस्याओं का सामना करना पड़ा। मैंने यह जाँचने का निर्णय लिया कि क्या यह सूत्र स्कूल क्षेत्र, शहर के सूक्ष्म जिलों और क्षेत्र के क्षेत्र को खोजने के लिए लागू है। और क्या समस्याओं को हल करने के लिए इसका उपयोग करना तर्कसंगत है।
अनुसंधान वस्तु: शिखर सूत्र।
शोध का विषय: समस्याओं को हल करने में पीक फॉर्मूला के आवेदन की तर्कसंगतता।
कार्य का उद्देश्य: चेकर पेपर पर चित्रित आंकड़ों के क्षेत्र को खोजने की समस्याओं को हल करते समय पिक फॉर्मूला का उपयोग करने की तर्कसंगतता की पुष्टि करना।
अनुसंधान के तरीके: मॉडलिंग, तुलना, सामान्यीकरण, सादृश्य, साहित्यिक और इंटरनेट संसाधनों का अध्ययन, विश्लेषण और सूचना का वर्गीकरण।
आवश्यक साहित्य का चयन करें, प्राप्त जानकारी का विश्लेषण और व्यवस्थित करें;
चेकर्ड पेपर पर समस्याओं को हल करने के लिए विभिन्न विधियों और तकनीकों पर विचार करें;
प्रायोगिक रूप से चुनें सूत्र का उपयोग करने की तर्कसंगतता की जांच करें;
इस सूत्र को लागू करने पर विचार करें।
परिकल्पना: यदि आप बहुभुज के क्षेत्रों को खोजने के लिए पीक फॉर्मूला लागू करते हैं, तो आप क्षेत्र का क्षेत्रफल पा सकते हैं, और चेकर पेपर पर समस्याओं को हल करना अधिक तर्कसंगत होगा।
मुख्य हिस्सा
सैद्धांतिक भाग
चेकर्ड पेपर (अधिक सटीक रूप से, इसके नोड्स), जिस पर हम अक्सर आकर्षित करना और आकर्षित करना पसंद करते हैं, एक विमान पर बिंदीदार जाली के सबसे महत्वपूर्ण उदाहरणों में से एक है। पहले से ही इस साधारण जाली ने के। गॉस के लिए एक सर्कल के क्षेत्र की तुलना करने के लिए एक प्रारंभिक बिंदु के रूप में कार्य किया, जिसके अंदर स्थित पूर्णांक निर्देशांक वाले बिंदुओं की संख्या है। तथ्य यह है कि एक विमान पर आंकड़ों के बारे में कुछ सरल ज्यामितीय बयानों का अंकगणितीय अध्ययन में गहरा परिणाम होता है, जी मिंकोव्स्की ने 1896 में स्पष्ट रूप से नोट किया था, जब उन्होंने पहली बार संख्या-सैद्धांतिक समस्याओं पर विचार करने के लिए ज्यामितीय तरीकों का इस्तेमाल किया था।
आइए चेकर पेपर पर एक बहुभुज बनाएं (परिशिष्ट 1, चित्र 1)। आइए अब इसके क्षेत्रफल की गणना करने का प्रयास करें। यह कैसे करना है? संभवत: सबसे आसान तरीका यह है कि इसे समकोण त्रिभुजों और एक समलंब चतुर्भुज में विभाजित किया जाए, जिसके क्षेत्रों की गणना करना और परिणामों को जोड़ना पहले से ही आसान है।
उपयोग की जाने वाली विधि सरल है, लेकिन बहुत बोझिल है; इसके अलावा, यह सभी बहुभुजों के लिए उपयुक्त नहीं है। इसलिए अगले बहुभुज को समकोण त्रिभुजों में विभाजित नहीं किया जा सकता है, जैसा कि हमने पिछले मामले में किया था (परिशिष्ट 2, चित्र 2)। उदाहरण के लिए, आप इसे "अच्छे" के साथ पूरक करने का प्रयास कर सकते हैं, जिसकी हमें आवश्यकता है, अर्थात, जिसका क्षेत्र हम वर्णित तरीके से गणना कर सकते हैं, फिर परिणामी संख्या से जोड़े गए भागों के क्षेत्रों को घटा सकते हैं।
हालांकि, यह पता चला है कि एक बहुत ही सरल सूत्र है जो आपको एक वर्ग ग्रिड के नोड्स पर ऐसे बहुभुजों के क्षेत्रों की गणना करने की अनुमति देता है।
इस सूत्र की खोज ऑस्ट्रियाई गणितज्ञ पिक जॉर्ज अलेक्जेंड्रोव (1859 - 1943) ने 1899 में की थी। इस सूत्र के अलावा, जॉर्ज पाइक ने पाइक, पाइक - जूलिया, पाइक - नेवलिना के प्रमेयों की खोज की, और श्वार्ज़ - पाइक असमानता को सिद्ध किया।
पीक के प्रकाशित होने के बाद कुछ समय के लिए इस सूत्र पर किसी का ध्यान नहीं गया, लेकिन 1949 में पोलिश गणितज्ञ ह्यूगो स्टीनहॉस ने अपने प्रसिद्ध गणितीय बहुरूपदर्शक में प्रमेय को शामिल किया। उस समय से, पिक का प्रमेय व्यापक रूप से जाना जाने लगा। जर्मनी में, पिक का सूत्र स्कूली पाठ्यपुस्तकों में शामिल है।
यह संयोजनीय ज्यामिति और संख्याओं की ज्यामिति का उत्कृष्ट परिणाम है।
पिक के सूत्र का प्रमाण
ABCD को ग्रिड लाइनों के साथ नोड्स और पक्षों पर शिखर के साथ एक आयत बनने दें (परिशिष्ट 3, चित्र 3)।
आइए हम В द्वारा निरूपित करें - आयत के अंदर स्थित नोड्स की संख्या, और द्वारा - इसकी सीमा पर नोड्स की संख्या। ग्रिड को आधा सेल दाईं ओर और आधा सेल में ले जाएँ
नीचे। फिर आयत के क्षेत्र को नोड्स के बीच "वितरित" किया जा सकता है: प्रत्येक बी नोड्स विस्थापित ग्रिड के पूरे सेल को "नियंत्रित" करता है, और प्रत्येक जी नोड्स - 4 बॉर्डर नॉन-कॉर्नर नोड्स - आधा सेल , और प्रत्येक कोने बिंदु - एक सेल का एक चौथाई। इसलिए, आयत S का क्षेत्रफल बराबर है
एस = बी + + 4 = बी + - 1 .
तो, ग्रिड लाइनों के साथ जाने वाले नोड्स और पक्षों पर कोने वाले आयतों के लिए, हम सूत्र S = B + - 1 सेट करते हैं . यह पिक का सूत्र है।
यह पता चला है कि यह सूत्र न केवल आयतों के लिए, बल्कि ग्रिड नोड्स पर कोने वाले मनमाने बहुभुजों के लिए भी सही है।
व्यावहारिक भाग
ज्यामितीय विधि और चयन सूत्र द्वारा आंकड़ों का क्षेत्रफल ज्ञात करना
मैंने यह सुनिश्चित करने का निर्णय लिया कि मेरे द्वारा देखे गए सभी उदाहरणों के लिए पिक का सूत्र सही था।
यह पता चला है कि यदि बहुभुज को ग्रिड नोड्स पर कोने के साथ त्रिकोण में काटा जा सकता है, तो इसके लिए पिक का सूत्र सही है।
मैंने 1 सेमी1 सेमी मापने वाले कोशिकाओं के साथ चेकर पेपर पर कुछ समस्याओं की समीक्षा की और समस्याओं को हल करने के लिए तुलनात्मक विश्लेषण किया (तालिका 1)।
तालिका 1 विभिन्न तरीकों से समस्याओं को हल करना।
चित्रकारी
ज्यामिति सूत्र द्वारा
शिखर सूत्र द्वारा
समस्या संख्या 1

एस = एसआदि - (2एस 1 + 2एस 2 )
एसआदि =4*5=20 सेमी 2
एस 1 =(2*1)/2=1 सेमी 2
एस 2 =(2*4)/2=4 सेमी 2
एस = 20- (2 * 1 + 2 * 4) = 10सेमी 2
उत्तर :10 सेमी ².
बी = 8, जी = 6
एस= 8 + 6/2 - 1 = 10 (सेमी²)
उत्तर: 10 सेमी²।
समस्या संख्या 2

ए = 2, एच = 4
एस = ए * एच = 2 * 4 = 8सेमी 2
उत्तर : 8 सेमी ².
बी = 6, जी = 6
एस= 6 + 6/2 - 1 = 8 (सेमी²)
उत्तर: 8 सेमी²।
समस्या संख्या 3

एस = एसवर्ग - (एस 1 + 2एस 2 )
एसवर्ग =4 2 =16 सेमी 2
एस 1 = (3 * 3)/2 = 4.5cm 2
एस 2 = (1 * 4) / 2 = 2 सेमी 2
एस= 16- (4.5 + 2 * 2) = 7.5 सेमी 2
बी = 6, जी = 5
एस= 6 + 5/2 - 1 = 7.5 (सेमी²)
उत्तर: 7.5 सेमी²।
समस्या संख्या 4

एस = एसआदि - (एस 1 + एस 2+ एस 3 )
एसआदि =4 * 3=12 सेमी 2
एस 1 =(3*1)/2=1,5 सेमी 2
एस 2 =(1*2)/2=1 सेमी 2
एस 3 =(1+3)*1/2=2 सेमी 2
एस = 12- (1.5 + 1 + 2) = 7.5सेमी 2
बी = 5, जी = 7
एस= 5 + 7/2 - 1 = 7.5 (सेमी²)
उत्तर: 7.5 सेमी²।
समस्या संख्या
5.

एस = एसआदि - (एस 1 + एस 2+ एस 3 )
एसआदि =6 * 5=30 सेमी 2
एस 1 =(2*5)/2=5 सेमी 2
एस 2 =(1*6)/2=3 सेमी 2
एस 3 =(4*4)/2=8 सेमी 2
एस = 30- (5 + 3 + 8) = 14सेमी 2
उत्तर: 14 सेमी²
एच = 12, जी = 6
एस= 12 + 6/2 - 1 = 14 (सेमी²)
उत्तर: 14 सेमी²
टास्क
№6.

एसटीआर = (4 + 9) / 2 * 3 = 19.5 सेमी 2
उत्तर: 19.5 सेमी 2
एच = 12, जी = 17
एस= 12 + 17/2 - 1 = 19.5 (सेमी²)
उत्तर: 19.5 सेमी 2
टास्क
№7.
1 सेमी - 200 मीटर के पैमाने पर एक वर्ग ग्रिड 1 × 1 (सेमी) के साथ योजना पर दिखाए गए जंगल का क्षेत्रफल (एम² में) पाएं
एस = एस 1 + एस 2+ एस 3
एस 1 =(800*200)/2=80000 एम 2
एस 2 =(200*600)/2=60000 एम 2
एस 3 =(800+600)/2*400=
280000 एम 2
एस = 80000+60000+240000=
420000m 2
उत्तर: 420,000 वर्ग मीटर
बी = 8, जी = 7. एस= 8 + 7/2 - 1 = 10.5 (सेमी²)
1 सेमी² - 200² वर्ग मीटर; एस= 40,000 10.5 = 420,000 (एम2)
उत्तर: 420,000 वर्ग मीटर
समस्या संख्या 8 ... 1 × 1 (सेमी) के पैमाने पर एक वर्ग ग्रिड के साथ योजना पर दर्शाए गए क्षेत्र का क्षेत्रफल (m² में) ज्ञात करें
1 सेमी - 200 मीटर। 
एस= एसवर्ग -2 ( एसटीआर + एससीढ़ी)
एसवर्ग। = 800 * 800 = 640,000 मी 2
एस tr = (200 * 600) / 2 = 60000m 2
एससीढ़ी = (200 + 800) / 2 * 200 =
100000m 2
एस=640000-2(60000+10000)=
320,000 मी 2
उत्तर: 320,000 वर्ग मीटर
समाधान।पाना एसपिक सूत्र का उपयोग करके चेकर पेपर पर दर्शाए गए चतुर्भुज का क्षेत्रफल:एस= बी + - 1
बी = 7, जी = 4। एस= 7 + 4/2 - 1 = 8 (सेमी²)
1 सेमी² - 200² वर्ग मीटर; एस= 40,000 8 = 320,000 (एम2)
उत्तर: 320,000 वर्ग मीटर
समस्या संख्या 9 ... क्षेत्र खोजेंएस 1 के बराबर वर्ग कोशिकाओं की भुजाओं पर विचार करते हुए सेक्टर, अपने उत्तर में इंगित करें .
एक त्रिज्यखंड एक वृत्त का एक चौथाई है और इसलिए इसका क्षेत्रफल एक वृत्त के क्षेत्रफल के एक चौथाई के बराबर है। एक वृत्त का क्षेत्रफल . होता हैआर 2 , कहाँ पे आर वृत्त की त्रिज्या है। हमारे मामले मेंआर =√5 और इसलिए क्षेत्रएस सेक्टर 5π / 4 है। कहांएस/ = 1.25.
उत्तर। 1.25
जी = 5, बी = 2, एस= बी + जी / 2 - 1 = 2 + 5/2 - 1 = 3.5, ≈ 1,11
उत्तर। 1.11.
समस्या संख्या 10. क्षेत्र खोजें एस वलय, वर्ग कोशिकाओं की भुजाओं को 1 के बराबर गिनते हुए। अपने उत्तर में, इंगित करें .
रिंग का क्षेत्रफल बाहरी और आंतरिक मंडलियों के क्षेत्रों के बीच के अंतर के बराबर है। RADIUSआर बाहरी वृत्त है
2, त्रिज्या आर आंतरिक वृत्त 2 है। इसलिए, वलय का क्षेत्रफल 4 . हैऔर इसलिए... उत्तर - 4।
जी = 8, बी = 8, एस= बी + जी / 2 - 1 = 8 + 8/2 - 1 = 11, ≈ 3,5
उत्तर: 3.5
निष्कर्ष: विचार किए गए कार्य गणित में परीक्षा के नियंत्रण और माप सामग्री के विकल्पों में से कार्य के समान हैं (कार्य संख्या 5,6)।
समस्याओं के सुविचारित समाधानों से, मैंने देखा कि उनमें से कुछ, उदाहरण के लिए, समस्या संख्या 2.6, ज्यामितीय सूत्रों का उपयोग करके हल करना आसान है, क्योंकि चित्र से ऊंचाई और आधार निर्धारित किया जा सकता है। लेकिन अधिकांश कार्यों में, आकृति को सरल (कार्य संख्या 7) या एक आयत (कार्य संख्या 1,4,5), एक वर्ग (कार्य संख्या 3,8) में पूर्ण निर्माण में विभाजित करना आवश्यक है।
समस्या # 9 और # 10 को हल करने से, मैंने देखा कि पिक के सूत्र को उन आकृतियों पर लागू करने से जो बहुभुज नहीं हैं, एक अनुमानित परिणाम देता है।
पीक फॉर्मूले की तर्कसंगतता की जाँच करने के लिए, मैंने बिताए समय के विषय पर एक अध्ययन किया (परिशिष्ट 4, तालिका 2)।
निष्कर्ष: तालिका और आरेख (परिशिष्ट 4, आरेख 1) से यह देखा जा सकता है कि पीक फॉर्मूला का उपयोग करके समस्याओं को हल करते समय बहुत कम समय व्यतीत होता है।
स्थानिक आकृतियों का पृष्ठीय क्षेत्रफल ज्ञात करना
आइए इस सूत्र की स्थानिक रूपों पर प्रयोज्यता की जाँच करें (परिशिष्ट 5, चित्र 4)।
वर्ग कोशिकाओं के किनारों को 1 मानते हुए, एक आयताकार समानांतर चतुर्भुज के कुल सतह क्षेत्र का पता लगाएं।
यह सूत्र का दोष है।
क्षेत्र का क्षेत्रफल ज्ञात करने के लिए शिखर सूत्र का अनुप्रयोग
व्यावहारिक सामग्री के साथ समस्याओं को हल करना (कार्य संख्या 7,8; तालिका संख्या 1), मैंने अपने स्कूल के क्षेत्र का पता लगाने के लिए इस पद्धति को लागू करने का निर्णय लिया, उस्त-इलिम्स्क, इरकुत्स्क शहर के माइक्रोडिस्ट्रिक्ट्स क्षेत्र।
"उस्त-इलिम्स्क में भूमि भूखंड मौसोश नंबर 11 की सीमाओं की परियोजना" (परिशिष्ट 6) की समीक्षा करने के बाद, मैंने अपने स्कूल के क्षेत्र का क्षेत्र पाया और इसकी तुलना क्षेत्र की मसौदा सीमाओं के अनुसार क्षेत्र के साथ की। भूमि भूखंड (परिशिष्ट 9, तालिका 3)।
उस्त-इलिम्स्क (परिशिष्ट 7) के दाहिने किनारे के हिस्से के नक्शे की जांच करने के बाद, मैंने सूक्ष्म जिलों के क्षेत्रों की गणना की और उनकी तुलना "उस्त-इलिम्स्क, इरकुत्स्क क्षेत्र की सामान्य योजना" के आंकड़ों से की। परिणाम तालिका में प्रस्तुत किए गए हैं (परिशिष्ट 9, तालिका 4)।
इरकुत्स्क क्षेत्र (परिशिष्ट 7) के नक्शे की जांच करने के बाद, मैंने क्षेत्र का क्षेत्र पाया और इसकी तुलना विकिपीडिया के आंकड़ों से की। परिणाम तालिका में प्रस्तुत किए गए हैं (परिशिष्ट 9, तालिका 5)।
परिणामों का विश्लेषण करने के बाद, मैं इस निष्कर्ष पर पहुंचा: पीक फॉर्मूला का उपयोग करके, इन क्षेत्रों को बहुत आसान पाया जा सकता है, लेकिन परिणाम अनुमानित हैं।
किए गए शोध से, मुझे स्कूल क्षेत्र (परिशिष्ट 10, आरेख 2) के क्षेत्र का पता लगाने पर सबसे सटीक मूल्य प्राप्त हुआ। इरकुत्स्क क्षेत्र (परिशिष्ट 10, आरेख 3) के क्षेत्र को खोजने पर परिणामों में अधिक विसंगति प्राप्त हुई थी। यह इस तथ्य के कारण है। यह कि सभी क्षेत्र की सीमाएँ बहुभुज पक्ष नहीं हैं, और कोने लंगर बिंदु नहीं हैं।
निष्कर्ष
अपने काम के परिणामस्वरूप, मैंने चेकर पेपर पर समस्याओं को हल करने के अपने ज्ञान का विस्तार किया, अध्ययन के तहत समस्याओं का वर्गीकरण अपने लिए निर्धारित किया।
कार्य करते समय, दो तरह से चेकर पेपर पर दर्शाए गए बहुभुजों के क्षेत्र को खोजने के लिए समस्याओं का समाधान किया गया: ज्यामितीय और पिक फॉर्मूला का उपयोग करना।
समाधानों का विश्लेषण और खर्च किए गए समय को निर्धारित करने के लिए एक प्रयोग से पता चला है कि सूत्र के आवेदन से बहुभुज के क्षेत्र को अधिक तर्कसंगत तरीके से खोजने के लिए समस्याओं को हल करना संभव हो जाता है। इससे गणित की परीक्षा में समय की बचत होती है।
चेकर्ड पेपर पर दर्शाए गए विभिन्न आंकड़ों के क्षेत्र को खोजने से यह निष्कर्ष निकालना संभव हो गया कि एक गोलाकार क्षेत्र और अंगूठी के क्षेत्र की गणना करने के लिए पिक के सूत्र का उपयोग अव्यावहारिक है, क्योंकि यह अनुमानित परिणाम देता है, और वह पिक का सूत्र अंतरिक्ष में समस्याओं को हल करने के लिए उपयोग नहीं किया जाता है।
साथ ही कार्य में विभिन्न प्रदेशों के क्षेत्र पीक फार्मूले का प्रयोग करते हुए पाये गये। हम यह निष्कर्ष निकाल सकते हैं कि विभिन्न क्षेत्रों का क्षेत्रफल ज्ञात करने के लिए सूत्र का उपयोग करना संभव है, लेकिन परिणाम अनुमानित हैं।
मेरे द्वारा प्रस्तुत परिकल्पना की पुष्टि हुई।
मैं इस निष्कर्ष पर पहुंचा कि जिस विषय में मेरी दिलचस्पी है वह काफी बहुआयामी है, चेकर पेपर पर कार्य विविध हैं, उनके समाधान के तरीके और तकनीक भी विविध हैं। इसलिए, मैंने इस दिशा में काम करना जारी रखने का फैसला किया।
साहित्य
वोल्कोव एसडी .. भूमि भूखंड की मसौदा सीमाएं, 2008, पी। सोलह.
गोरिना एल.वी., गणित। शिक्षक के लिए सब कुछ, एम: नौका, 2013, नंबर 3, पी। 28.
प्रोकोपयेवा वी.पी., पेट्रोव ए.जी., उस्त-इलिम्स्क शहर की सामान्य योजना, इरकुत्स्क क्षेत्र, रूस के गोस्ट्रोय, 2004 पी। 65.
Riss E.A., Zharkovskaya N.M., चेकर्ड पेपर की ज्यामिति। पिक का फॉर्मूला। - मॉस्को, 2009, नंबर 17, पी। 24-25.
स्मिरनोवा आई एम। स्मिरनोव वी। ए, चेकर पेपर पर ज्यामिति। - मॉस्को, चिश्ये प्रूडी, 2009, पी। 120.
स्मिरनोवा आई.एम., स्मिरनोव वी.ए., व्यावहारिक सामग्री के साथ ज्यामितीय समस्याएं। - मॉस्को, चिश्ये प्रूडी, 2010, पी। 150
FIPI, 2015 के गणित में कार्यों के खुले बैंक की समस्याएं।
Ust-Ilimsk शहर का नक्शा।
इरकुत्स्क क्षेत्र का नक्शा.
विकिपीडिया.
पीक फॉर्मूला
1 परिचय
2. पिक का फॉर्मूला। आई का प्रमाण।
प्रमाण द्वितीय।
श्री का प्रमाण।
3. कार्य।
4. कोने के निर्देशांक के माध्यम से बहुभुज के क्षेत्र के लिए सूत्र।
5. कार्य।
6. साहित्य
पिक का फॉर्मूला।
1 परिचय।
हम इतिहास से ज्ञान लेते हैं,
कविता में - बुद्धि,
गणित में, विवेक।
एफ बेकन
प्लॉट चेकर पेपर के एक नियमित टुकड़े पर प्रकट होगा।
कोशिकाओं के किनारों के साथ चलने वाली रेखाएं एक ग्रिड बनाती हैं, और कोशिकाओं के कोने इस ग्रिड के नोड बनाते हैं। आइए शीट पर नोड्स पर कोने के साथ एक बहुभुज बनाएं और उसका क्षेत्रफल ज्ञात करें।
आप इसे अलग-अलग तरीकों से खोज सकते हैं। उदाहरण के लिए, आप एक बहुभुज को काफी सरल आकृतियों में काट सकते हैं, उनका क्षेत्रफल ज्ञात कर सकते हैं और उन्हें मोड़ सकते हैं।
लेकिन यहां हम बहुत परेशानी में हैं। एक आकृति को आसानी से आयतों, समलम्ब चतुर्भुजों और त्रिभुजों में विभाजित किया जा सकता है, और इसके क्षेत्रफल की गणना सहजता से की जाती है।
हालांकि बहुभुज काफी सरल दिखता है, इसके क्षेत्रफल की गणना करने में बहुत काम लगेगा। क्या होगा यदि बहुभुज अधिक विचित्र लगे? यह पता चला है कि बहुभुज के क्षेत्र जिनके कोने ग्रिड के नोड्स पर स्थित हैं, की गणना बहुत आसान की जा सकती है: एक सूत्र है जो उनके क्षेत्र को अंदर और बहुभुज की सीमा पर स्थित नोड्स की संख्या से जोड़ता है। इस अद्भुत और सरल सूत्र को पिक का सूत्र कहते हैं।
2. पिक का फॉर्मूला।
एक बहुभुज के कोने (जरूरी नहीं कि उत्तल हो) एक पूर्णांक जाली के नोड्स पर स्थित होते हैं। इसके अंदर जाली के बी नोड्स और नोड्स की सीमा पर स्थित है। आइए हम सिद्ध करें कि इसका क्षेत्रफल B + . के बराबर है  - 1 (चुनने का सूत्र)।
- 1 (चुनने का सूत्र)।
आई का प्रमाण।
एक बहुभुज पर विचार करें जिसके शीर्ष एक पूर्णांक जालक के नोड्स पर हैं, अर्थात उनके पास पूर्णांक निर्देशांक हैं।

बहुभुज को जाली के नोड्स पर शीर्षों के साथ त्रिभुजों में विभाजित करें, जिसमें अंदर या किनारों पर नोड्स नहीं होते हैं।

आइए निरूपित करें:
एन- बहुभुज के पक्षों की संख्या,
एम- जाली के नोड्स पर कोने वाले त्रिभुजों की संख्या जिनमें नोड्स या तो अंदर या किनारों पर नहीं होते हैं,
बी - बहुभुज के अंदर नोड्स की संख्या,
कोने सहित पक्षों पर नोड्स की संख्या है।
इन सभी त्रिभुजों के क्षेत्रफल समान और समान हैं।
इसलिए, बहुभुज का क्षेत्रफल है  .
.
180 0 एम .
आइए अब इस राशि को दूसरे तरीके से खोजें।
किसी भी आंतरिक नोड पर शीर्ष वाले कोणों का योग 360 0 होता है।
फिर सभी आंतरिक नोड्स पर कोने वाले कोणों का योग 360 0 V है।
पक्षों पर नोड्स पर कोणों का कुल योग, लेकिन शिखर पर नहीं 180 0 के बराबर है (Г - एन).
बहुभुज के शीर्षों पर कोणों का योग 180 0 है ( एन – 2) .
सभी त्रिभुजों के कोणों का कुल योग होता है 360 0 वी + 180 0 (जी - एन) + 180 0 (एन – 2).
इस प्रकार, 180 0 एम= 360 0 वी + 180 0 (जी - एन) + 180 0 (एन – 2),
180 0 एम= 360 0 वी + 180 0 जी - 180 0 एन + 180 0 एन- 180 0 2,
180 0 एम= 360 0 वी + 180 0 जी - 360 0,
 = बी +
= बी +  – 1 ,
– 1 ,
जहाँ से हमें बहुभुज के क्षेत्रफल S का व्यंजक प्राप्त होता है:
एस= बी +  – 1 ,
– 1 ,
पिक सूत्र के रूप में जाना जाता है।
चित्र में: एच = 24, जी = 9, इसलिए,एस = 24 + – 1 = 27,5.

पिक सूत्र का उपयोग करके पहले बहुभुज का क्षेत्रफल ज्ञात कीजिए:

बी = 28 (हरा बिंदु);
जी = 20 (नीला बिंदु)।
हम पाते हैं, एस =  = 37 वर्ग इकाई
= 37 वर्ग इकाई
प्रमाण द्वितीय।
पूर्णांक जाली के नोड्स पर शीर्षों के साथ प्रत्येक बहुभुज M के लिए, हम संख्या f (M) = निर्दिष्ट करते हैं  , जहां एम से संबंधित सभी जाली नोड्स पर योग किया जाता है, और कोण
, जहां एम से संबंधित सभी जाली नोड्स पर योग किया जाता है, और कोण  निम्नानुसार परिभाषित किया गया है:
निम्नानुसार परिभाषित किया गया है:  =
=  बहुभुज के आंतरिक बिंदु के लिए,
बहुभुज के आंतरिक बिंदु के लिए,  =
=  एक शीर्ष के अलावा एक सीमा बिंदु के लिए, और
एक शीर्ष के अलावा एक सीमा बिंदु के लिए, और  - शीर्ष पर कोण, यदि दिया गया नोड एक शीर्ष है। यह देखना आसान है कि f (M) =
- शीर्ष पर कोण, यदि दिया गया नोड एक शीर्ष है। यह देखना आसान है कि f (M) =  +
+  = बी +
= बी +  - 1. यह जांचना बाकी है कि संख्या f (M) बहुभुज M के क्षेत्रफल के बराबर है।
- 1. यह जांचना बाकी है कि संख्या f (M) बहुभुज M के क्षेत्रफल के बराबर है।
बहुभुज एम को बहुभुज एम 1 और एम 2 में जाली नोड्स पर शिखर के साथ काटने दें। तब f (M) = f (M 1) + f (M 2), क्योंकि कोण प्रत्येक नोड के लिए योग करते हैं। इसलिए, यदि दो बहुभुज M, M 1 और M 2 के लिए पिक का सूत्र सत्य है, तो यह तीसरे के लिए भी सत्य है।
यदि M भुजाओं वाला एक आयत है पीतथा क्यूजाली रेखाओं के साथ निर्देशित, फिर
एफ (एम) = (पी -1) (क्यू -1) +  = पीक्यू।
= पीक्यू।
इस मामले में, पिक का सूत्र मान्य है। आयत M को विकर्ण के साथ त्रिभुज M 1 और M 2 में काटना और इस तथ्य का उपयोग करना कि f (M) = f (M 1) + f (M 2) और f (M 1) = f (M 2), यह आसान है। जाली रेखाओं के साथ निर्देशित पैरों के साथ किसी भी समकोण त्रिभुज के लिए पिक फॉर्मूला साबित करने के लिए। इनमें से कई त्रिभुजों को एक आयत से काटकर, आप कोई भी त्रिभुज प्राप्त कर सकते हैं।

पिक के सूत्र के प्रमाण को पूरा करने के लिए, यह ध्यान रखना बाकी है कि किसी भी बहुभुज को विकर्णों को अलग करके त्रिभुजों में काटा जा सकता है।
श्री का प्रमाण।
एक आकृति के क्षेत्र और इस आकार में आने वाले नोड्स की संख्या के बीच संबंध एक आयत के मामले में विशेष रूप से स्पष्ट है।

होने देना ए बी सी डी- ग्रिड लाइनों के साथ नोड्स और किनारों पर शिखर के साथ एक आयत।
आइए हम द्वारा निरूपित करें वीआयत के अंदर और बाद में स्थित नोड्स की संख्या जी- इसकी सीमा पर नोड्स की संख्या। ग्रिड को आधा सेल दाईं ओर और आधा सेल नीचे ले जाएँ।

फिर आयत के क्षेत्र को नोड्स के बीच "वितरित" किया जा सकता है: प्रत्येक वीनोड्स विस्थापित ग्रिड के पूरे सेल को "नियंत्रित" करते हैं, जिनमें से प्रत्येक जी- 4 बॉर्डर नॉन-कॉर्नर नोड्स - आधा सेल, और प्रत्येक कॉर्नर पॉइंट - सेल का एक चौथाई। इसलिए, आयत S का क्षेत्रफल बराबर है

तो, ग्रिड लाइनों के साथ जाने वाले नोड्स और पक्षों पर कोने वाले आयतों के लिए, हम सूत्र सेट करते हैं 
आइए हम साबित करें कि यह सूत्र न केवल आयतों के लिए मान्य है, बल्कि ग्रिड नोड्स पर कोने वाले मनमाने बहुभुजों के लिए भी मान्य है।
आइए हम द्वारा निरूपित करें एस
एम
बहुभुज क्षेत्रएम
नोड्स पर कोने के साथ, और के माध्यम सेपी
एम
- मूल्य  , कहाँ पेवी
एम
- अंदर नोड्स की संख्याएम,ए जी
एम
- सीमा पर नोड्स की संख्या। तब पिक का सूत्र इस प्रकार लिखा जा सकता है
, कहाँ पेवी
एम
- अंदर नोड्स की संख्याएम,ए जी
एम
- सीमा पर नोड्स की संख्या। तब पिक का सूत्र इस प्रकार लिखा जा सकता है  .
.
हमने सूत्र के प्रमाण को कई चरणों में विभाजित किया है।
स्टेप 1।
यदि बहुभुजएम
ग्रिड नोड्स पर कोने के साथ 2 बहुभुजों में काटा जाता हैएम
1
तथा एम
2
,
केवल ग्रिड नोड्स पर भी शिखर होते हैं, तब  ... चलो बहुभुजएम
बहुभुज में काटेंएम
1
तथा एम
2
खंड द्वारा नोड्स पर कोने के साथएबी. सेगमेंट पर आने वाले नोड्स को छोड़कर सभी नोड्सएबी,
सूत्र के बाएँ और दाएँ पक्षों को समान योगदान दें। खंड AB पर स्थित नोड्स पर विचार करें।
... चलो बहुभुजएम
बहुभुज में काटेंएम
1
तथा एम
2
खंड द्वारा नोड्स पर कोने के साथएबी. सेगमेंट पर आने वाले नोड्स को छोड़कर सभी नोड्सएबी,
सूत्र के बाएँ और दाएँ पक्षों को समान योगदान दें। खंड AB पर स्थित नोड्स पर विचार करें।

यदि ऐसा नोड ए और बी (उदाहरण के लिए, सी) के बीच स्थित है, तो बहुभुज के लिएएम
यह आंतरिक है, लेकिन बहुभुज के लिएएम
1
तथा एम
2
- सीमा। इसलिए, उनका योगदानपी
एम
1 के बराबर है, और प्रत्येक भाव में  तथा
तथा 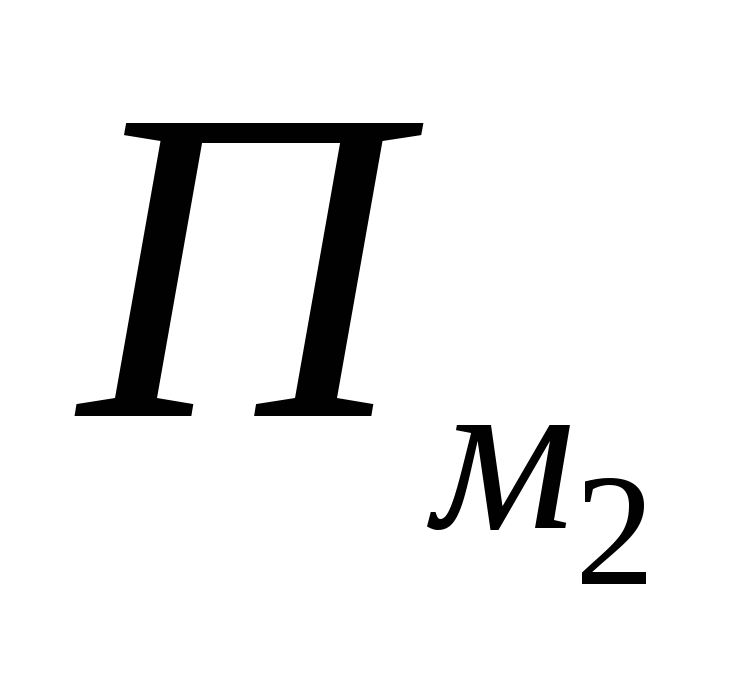 - 0.5 प्रत्येक, यानी ऐसे नोड का योगदानपी
एम
तथा
- 0.5 प्रत्येक, यानी ऐसे नोड का योगदानपी
एम
तथा  बराबर हैं।
बराबर हैं।
नोड्स ए और बी पर विचार करें। वे सीमा के रूप में हैं एमऔर किसके लिए एम 1 , एम 2 .
इसलिए, इनमें से प्रत्येक नोड का योगदानपी
एम
0.5 एक इंच . के बराबर है  -
इकाई। इसलिए, नोड्स ए और बी का कुल योगदानपी
एम
1 के बराबर है, जो उनके योगदान से 1 कम है
-
इकाई। इसलिए, नोड्स ए और बी का कुल योगदानपी
एम
1 के बराबर है, जो उनके योगदान से 1 कम है  .
लेकिन
.
लेकिन  , ए ।
, ए ।
सभी नोड्स के कुल "योगदान" से पी एम 1 घटाता है, और से  2 घटाएं, और यह नोड्स ए और बी के योगदान में अंतर के लिए क्षतिपूर्ति करता है।
2 घटाएं, और यह नोड्स ए और बी के योगदान में अंतर के लिए क्षतिपूर्ति करता है।
इसलिए,  .
.
चरण दो।
यदि बहुभुज एमजाल बिंदुओं पर शिखर के साथ दो बहुभुजों में काटा जाता है एम 1 तथा एम 2 (नोड्स पर कोने के साथ भी) और कुछ दो बहुभुजों के लिए सूत्र सही है मिमी 1 , एम 2 , तो यह तीसरे बहुभुज के लिए भी सत्य है।
उदाहरण के लिए, इसे सत्य होने देंएम
1
तथा एम
2
,
अर्थात्  ... फिर (पहले चरण के अनुसार),
लेकिन पर
पहला चरण) अंतिम अभिव्यक्ति हैपी
एम
,
और समानता
... फिर (पहले चरण के अनुसार),
लेकिन पर
पहला चरण) अंतिम अभिव्यक्ति हैपी
एम
,
और समानता  और पीक का सूत्र है।
और पीक का सूत्र है।
चरण 3।
आइए हम एक समकोण त्रिभुज के लिए पिक फॉर्मूला साबित करें जिसमें ग्रिड नोड्स और पैर ग्रिड लाइनों पर स्थित हों।
त्रिकोण एबीसीआयताकार बनाने के लिए ए बी सी डी .

आयतों के लिए, पिक का सूत्र सही है: एस ए बी सी डी = पी ए बी सी डी . पहले चरण के अनुसार पी ए बी सी डी = पी एबीसी + पी एसीडी , पी एबीसी = पी एसीडी , इसलिए पी ए बी सी डी = 2पी एबीसी . लेकिन एस ए बी सी डी = 2 एस एबीसी ... इसलिए एस एबीसी = पी एबीसी .
चरण 4।
ग्रिड बिंदुओं पर शिखर के साथ एक मनमाना त्रिभुज के लिए पिक का सूत्र सही है।

आकृति को देखने के बाद, यह समझना आसान है: इस तरह के किसी भी त्रिकोण को कुछ आयत से "काटने" के द्वारा प्राप्त किया जा सकता है, जिसमें ग्रिड लाइनों के साथ कई आयतें और ग्रिड लाइनों पर पैरों के साथ समकोण त्रिभुज होते हैं। और चूँकि पिक का सूत्र आयतों और समकोण त्रिभुजों के लिए सत्य है, तो (चरण 2 को याद कीजिए) यह मूल त्रिभुज के लिए भी सत्य है।
हमने सिद्ध किया है कि यदि बहुभुज को ग्रिड नोड्स पर शीर्षों वाले त्रिभुजों में काटा जा सकता है, तो इसके लिए पिक का सूत्र सत्य है।
3. कार्य।
आकृतियों के क्षेत्रफल ज्ञात कीजिए:
1
.



![]()
बी = 9
जी = 4
![]()



![]()
बी = 9
जी = 5




![]()
नए लेख
- एक समारोह की मदद से वांछित गर्भावस्था कैसे प्राप्त करें जादू की मदद से बच्चे के जन्म का पता कैसे लगाएं
- ऑफिस में सोएं कांच की दीवारें
- महिलाओं के लिए गर्भावस्था कितने समय तक चलती है मां और बच्चे के लिए परिणाम
- चीनी स्मृति चिन्ह जो धन, सद्भाव और प्रेम खोजने में मदद करते हैं
- ड्रीम इंटरप्रिटेशन: डॉक्टर क्या सपना देख रहा है सपने में डॉक्टर होने का क्या मतलब है
- बेटी का नाम कैसे रखें: लड़की के लिए सबसे दुर्लभ, सबसे सुंदर और असामान्य नाम चुनें
- आराधनालय में शुक्र और बृहस्पति के पहलू
- चलती कुंडली - स्थानांतरण - निर्माण और व्याख्या की मूल बातें टेस्ट नेटल चार्ट
- पीआई क्या है और इसका क्या मतलब है?
- जन्मदिन के बारे में पूरा रहस्य
लोकप्रिय लेख
- नरक के राक्षसों के नामों की उत्पत्ति
- मृतक प्रियजन की आत्मा के साथ संचार
- शुक्र किस चीज से बनता है। शुक्र के बारे में संदेश। यह अन्य ग्रहों की तुलना में विपरीत दिशा में घूमता है।
- किसी व्यक्ति के जीवन और प्रतिष्ठा को कैसे खराब करें?
- आपको क्या ध्यान देना चाहिए
- जन्म तिथि के अनुसार राशिफल
- ताश खेलने पर सरल भाग्य बता रहा है - भविष्य और प्यार के लिए लेआउट
- ऑनलाइन ताश खेलने पर भाग्य बता रहा है
- दैनिक जीवन में पुरुषों, महिलाओं से, यौन रूप से, चुंबन के माध्यम से, रक्त के माध्यम से एचआईवी संक्रमण कैसे फैलता है
- क्लैमाइडिया के लिए हेलिकोबैक्टर पाइलोरी एंटीबॉडी के परीक्षण के परिणामों को कैसे समझें 1 5
