Proiect de cercetare „Formula pic în geometria hârtiei în carouri. Formula de vârf într-un curs de planimetrie școlară

Textul lucrării este postat fără imagini și formule.
Versiunea completa munca este disponibilă în fila „Fișiere de lucru” în format PDF

Introducere

Sunt elev in clasa a VI-a. Am început să studiez geometria anul trecut, pentru că studiez la școală folosind manualul „Matematică. Aritmetic. Geometrie” editată de E.A. Bunimovici, L.V. Kuznetsova, S.S. Minaeva și alții.

Subiectele care au atras cel mai mult atenția au fost „Zonele figurilor” și „Elaborarea formulelor”. Am observat că se găsesc zonele acelorași figuri căi diferite. În viața de zi cu zi, ne confruntăm adesea cu problema găsirii spațiului. De exemplu, găsiți zona podelei care va trebui vopsită. Este interesant de cumpărat suma necesară tapet pentru renovare, trebuie să știți dimensiunea camerei, adică. zona peretelui. Calcularea ariei unui pătrat, dreptunghi și triunghi dreptunghic nu mi-a cauzat dificultăți.

Devenind interesat de acest subiect, am început să caut material suplimentar pe internet. În urma căutărilor mele, am dat peste formula lui Pick - aceasta este o formulă pentru calcularea ariei unui poligon desenat pe hârtie în carouri. Mi s-a părut că calcularea suprafeței folosind această formulă este accesibilă oricărui student. De aceea am decis să conduc muncă de cercetare.

Relevanța subiectului:

Această temă este o completare și aprofundare a studiului cursului de geometrie.

Studierea acestui subiect vă va ajuta să vă pregătiți mai bine pentru olimpiade și examene.

Scopul lucrării:

Familiarizați-vă cu formula Peak.

Stăpânește tehnici de rezolvare a problemelor geometrice folosind formula Pick.

Sistematizați și rezumați materialele teoretice și practice.

Obiectivele cercetării:

Verificați eficacitatea și fezabilitatea utilizării formulei la rezolvarea problemelor.

Învață să aplici formula Peak în probleme de complexitate diferită.

Comparați problemele rezolvate folosind formula Pick și metoda tradițională.

Parte principală

1.1. Referință istorică

Georg Alexander Pieck - matematician austriac, născut la 10 august 1859. Era un copil dotat, a fost predat de tatăl său, care conducea un institut privat. La vârsta de 16 ani, Georg a absolvit școala și a intrat la Universitatea din Viena. La 20 de ani, a primit dreptul de a preda fizica si matematica. Formula sa de determinare a zonei unei rețele poligonale i-a adus faimă în întreaga lume. Și-a publicat formula într-un articol în 1899. A devenit popular atunci când omul de știință polonez Hugo Steinhaus a inclus-o într-o publicație din 1969 de instantanee matematice.

Georg Pieck a fost educat la Universitatea din Viena și și-a susținut doctoratul în 1880. După ce și-a luat doctoratul, a fost numit asistent al lui Ernest Mach la Universitatea Scherl-Ferdinand din Praga. Acolo a devenit profesor. A rămas la Praga până la pensionare în 1927 și apoi s-a întors la Viena.

Pick a prezidat comitetul de la Universitatea Germană din Praga care l-a numit pe Einstein ca profesor la departamentul de fizică matematică în 1911.

A fost ales membru al Academiei Cehe de Științe și Arte, dar a fost expulzat după ce naziștii au capturat Praga.

Când naziștii au intrat în Austria, pe 12 martie 1938, s-a întors la Praga. În martie 1939, naziștii au invadat Cehoslovacia. Pe 13 iulie 1942, Pieck a fost deportat în lagărul Theresienstadt, înființat de naziști în nordul Boemiei, unde a murit două săptămâni mai târziu, la vârsta de 82 de ani.

1.2. Cercetare și dovezi

Mi-am început munca de cercetare punând întrebarea: ce zone de figuri pot găsi? Scrieți o formulă pentru a calcula suprafața diferite triunghiurişi patrulatere am putut. Dar ce zici de cinci, șase și, în general, poligoane?

În timpul cercetărilor mele pe diverse site-uri, am văzut soluții la probleme care implică calcularea ariei a cinci, șase și alte poligoane. Formula care permite rezolvarea acestor probleme a fost numită formula lui Pick. Arata asa :S =B+G/2-1, Unde ÎN- numărul de noduri situate în interiorul poligonului, G- numărul de noduri situate la limita poligonului. Particularitatea acestei formule este că poate fi folosită numai pentru poligoane desenate pe hârtie în carouri.

Orice astfel de poligon poate fi ușor împărțit în triunghiuri cu vârfuri la nodurile rețelei și care nu conțin noduri nici în interior, nici pe laturi. Se poate demonstra că ariile tuturor acestor triunghiuri sunt aceleași și egale cu ½ și, prin urmare, aria poligonului este egală cu jumătate din numărul lor T.

Pentru a găsi acest număr, să notăm cu n numărul de laturi ale poligonului, cu ÎN- numărul de noduri din interiorul acestuia, prin G- numărul de noduri pe laturi, inclusiv vârfurile. valoare totală unghiurile tuturor triunghiurilor sunt de 180°. T.

Acum să găsim suma într-un alt mod.

Suma unghiurilor cu vârful la orice nod intern este 2,180°, adică. suma totală a unghiurilor este de 360°. ÎN; suma totală a unghiurilor pentru nodurile de pe laturi, dar nu de la vârfuri este ( G-n)180°, iar suma unghiurilor de la vârfurile poligonului va fi egală cu ( G- 2)180°. Prin urmare, T= 2.180°. B+(G-n)180°+(n -2)180 °. Deschizând parantezele și împărțind la 360°, obținem o formulă pentru aria S a unui poligon, cunoscută sub numele de formula lui Pick.

2. Partea practică

Am decis să testez această formulă pe sarcini din colecția OGE-2017. A luat probleme la calcularea ariei unui triunghi, patrulater și pentagon. Am decis să compar răspunsurile, rezolvând în două moduri: 1) am completat cifrele la un dreptunghi și am scăzut aria triunghiurilor dreptunghiulare din aria dreptunghiului rezultat; 2) a aplicat formula Pick.

S = 18-1,5-4,5 = 12 și S = 7+12/2-1= 12

S = 24-9-3 = 12 și S = 7+12/2-1 = 12

S = 77-7,5-12-4,5-4 =49 și S = 43+14/2-1 = 49

După ce am comparat rezultatele, ajung la concluzia că ambele formule dau același răspuns. Găsirea ariei unei figuri folosind formula lui Pick s-a dovedit a fi mai rapidă și mai ușoară, deoarece au fost mai puține calcule. Ușurința soluționării și economisirea timpului la calcule îmi vor fi de folos în viitor când iau OGE.

Acest lucru m-a determinat să verific posibilitatea aplicării formulei Pick la cifre mai complexe.

S = 0 + 4/2 -1 = 1

S = 5+11/2-1 = 9,5

S = 4+16/2-1 = 1

Concluzie

Formula Peak este ușor de înțeles și ușor de utilizat. În primul rând, este suficient să poți număra, împărți cu 2, adună și scădea. În al doilea rând, puteți găsi zona unei figuri complexe fără a petrece mult timp. În al treilea rând, această formulă funcționează pentru orice poligon.

Dezavantajul este că Formula Pick este aplicabilă doar pentru figurile care sunt desenate pe hârtie în carouri și ale căror vârfuri se află pe nodurile hârtiei în carouri.

Sunt sigur că la promovarea examenelor finale, problemele la calcularea ariei cifrelor nu vor crea dificultăți. La urma urmei, sunt deja familiarizat cu formula Peak.

Bibliografie

Bunimovici E.A., Dorofeev G.V., Suvorova S.B. si altele.Matematica. Aritmetic. Geometrie. Clasa a V-a: educațională. pentru învăţământul general organizatii cu adj. pe electron purtător - ed. a III-a - M.: Educație, 2014.- 223, p. : bolnav. - (Sfere).

Bunimovici E.A., Kuznetsova L.V., Minaeva S.S. si altele.Matematica. Aritmetic. Geometrie. Clasa a VI-a: educațională. pentru învăţământul general organizații-ed. a V-a-M.: Educație, 2016.-240 p. : bolnav.- (Sfere).

Vasiliev N.B. În jurul formulei Pick. //Kvant.- 1974.-Nr 2. -p.39-43

Rassolov V.V. Probleme de planimetrie. / Ed. a 5-a, rev. Și suplimentar - M.: 2006.-640s.

I.V. Iascenko.OGE. Matematică: variante standard de examen: O-39 36 opțiuni - M.: Editura " Educația națională", 2017. -240 p. - (OGE. FIPI-scoala).

„Voi rezolva OGE”: matematică. Sistemul de antrenament al lui Dmitri Gușchin. OGE-2017: sarcini, răspunsuri, soluții [Resursă electronică]. Mod de acces: https://oge.sdamgia.ru/test?id=6846966 (data acces 04/02/2017)

Folosind formula lui Pick, puteți găsi aria unei figuri construite pe o foaie de hârtie într-o cușcă (triunghi, pătrat, trapez, dreptunghi, poligon).

În problemele care vor fi la Examenul Unificat de Stat, există un întreg grup de sarcini în care este dat un poligon, construit pe o foaie de hârtie într-un pătrat și întrebarea este despre găsirea zonei. Scara celulei este de un centimetru pătrat.

Vizualizați conținutul prezentării

Georg Pick

Georg Alexander Pick,

matematician austriac

(10.08.1859 - 13.07.1942)

Formula a fost descoperită în 1899.

Zona figurii dorite poate fi găsită folosind formula:

M – numărul de noduri de pe marginea triunghiului (pe laturi și vârfuri):
N – numărul de noduri din interiorul triunghiului;

* Prin „noduri” înțelegem intersecția liniilor.

Să găsim aria triunghiului:

Să marchem nodurile:

1 celulă = 1 cm

M = 15 (indicat cu roșu)
N=34 (în albastru)

Să găsim aria paralelogramului:

Să marchem nodurile:

M = 18 (indicat cu roșu)
N = 20 (în albastru)

Să găsim aria trapezului:

Să marchem nodurile:

M = 24 (indicat cu roșu)
N = 25 (în albastru)

Să găsim aria poligonului:

Să marchem nodurile:

M = 14 (indicat cu roșu)
N=43 (în albastru)

Să marchem nodurile:

M = 11 (indicat cu roșu)
N = 5 (în albastru)

Decideți singuri:

1. Găsiți aria unui patrulater reprezentat pe hârtie în carouri cu o dimensiune a celulei de 1 cm x 1 cm. Dați răspunsul în centimetri pătrați.

4. Găsiți aria unui patrulater reprezentat pe hârtie în carouri cu dimensiunea celulei de 1 cm x 1 cm. Dați răspunsul în centimetri pătrați .

Să desenăm un dreptunghi în jurul lui:

Din zona dreptunghiului (in în acest caz, acesta este un pătrat) scădeți ariile figurilor simple rezultate:

Raspunsuri:

№ sarcini

Opțiunea 1

Opțiunea 2

Opțiunea 3

Opțiunea 4

Formula lui Pick

Sazhina Valeria Andreevna, Elev în clasa a IX-a a MAOU „Școala Gimnazială Nr. 11” din Ust-Ilimsk, regiunea Irkutsk

supraveghetor: Gubar Oksana Mihailovna, profesor de matematică cu cea mai înaltă categorie de calificare, MAOU „Școala secundară nr. 11”, Ust-Ilimsk, regiunea Irkutsk

2016

Introducere

În timp ce studiam subiectul de geometrie „Areele poligoanelor”, am decis să aflu: există o modalitate de a găsi zone care să fie diferite de cele pe care le-am studiat la clasă?

Această metodă este formula Pick. L.V. Gorina în „Materiale pentru autoeducarea elevilor” a descris această formulă astfel: „Familiarizarea cu formula Peak este deosebit de importantă cu o zi înainte. promovarea examenului de stat unificatși GIA. Folosind această formulă, puteți rezolva cu ușurință o clasă mare de probleme oferite la examene - acestea sunt probleme de găsire a zonei unui poligon reprezentat pe hârtie în carouri. Mica formulă a lui Pick va înlocui întregul set de formule necesare pentru a rezolva astfel de probleme. Formula Peak va funcționa „unul pentru toți...”!”

În materialele pentru examenul de stat unificat am întâlnit probleme cu conținut practic privind găsirea suprafeței terenurilor. Am decis să verific dacă această formulă este aplicabilă pentru găsirea zonei teritoriului școlar, microdistricte ale orașului, regiune. Și este rațional să-l folosești pentru a rezolva probleme?

Obiectul de studiu: formula lui Pick.

Obiectul cercetării: aplicarea rațională a formulei Pick în rezolvarea problemelor.

Scopul lucrării: a fundamenta raționalitatea utilizării formulei Pick la rezolvarea problemelor de găsire a zonei figurilor reprezentate pe hârtie în carouri.

Metode de cercetare: modelare, comparare, generalizare, analogii, studiul resurselor literare și internetului, analiza și clasificarea informațiilor.

Selectează literatura necesară, analizează și sistematizează informațiile primite;

Considera diverse metodeși tehnici de rezolvare a problemelor pe hârtie în carouri;

Verifica experimental raționalitatea utilizării formulei Pick;

Luați în considerare aplicarea acestei formule.

Ipoteza: dacă aplicați formula lui Pick pentru a găsi aria unui poligon, puteți găsi aria teritoriului, iar rezolvarea problemelor pe hârtie în carouri va fi mai rațională.

Parte principală

Partea teoretică

Hârtia în carouri (mai precis, nodurile sale), pe care preferăm adesea să desenăm și să desenăm, este unul dintre cele mai importante exemple de rețea cu puncte pe un plan. Deja această rețea simplă a servit ca punct de plecare pentru K. Gauss pentru a compara aria unui cerc cu numărul de puncte cu coordonate întregi situate în interiorul acestuia. Faptul că unele afirmații geometrice simple despre figurile de pe plan au consecințe profunde în cercetarea aritmetică a fost observat în mod explicit de G. Minkowski în 1896, când a folosit pentru prima dată metode geometrice pentru a lua în considerare problemele teoretice ale numerelor.

Să desenăm un poligon pe hârtie în carouri (Anexa 1, Figura 1). Să încercăm acum să-i calculăm aria. Cum să o facă? Probabil cea mai ușoară modalitate este de a o împărți în triunghiuri dreptunghiulare și un trapez, ale căror zone sunt ușor de calculat și de adunat rezultatele.

Metoda folosită este simplă, dar foarte greoaie și, în plus, nu este potrivită pentru toate poligoanele. Deci următorul poligon nu poate fi împărțit în triunghiuri dreptunghiulare, așa cum am făcut acest lucru în cazul precedent (Anexa 2, Figura 2). Putem, de exemplu, să încercăm să-l suplimentăm celui „bun” de care avem nevoie, adică celui a cărui arie o putem calcula în modul descris, apoi scădem ariile părților adăugate din numărul rezultat.

Cu toate acestea, se dovedește că există o formulă foarte simplă care vă permite să calculați ariile unor astfel de poligoane cu vârfuri la nodurile unei grile pătrate.

Această formulă a fost descoperită de matematicianul austriac Peak Georg Alexandrov (1859 - 1943) în 1899. În plus față de această formulă, Georg Pick a descoperit teoremele Pick, Pick-Julia, Pick-Nevalina și a demonstrat inegalitatea Schwartz-Pick.

Această formulă a trecut neobservată de ceva timp după ce Pick a publicat-o, dar în 1949, matematicianul polonez Hugo Steinhaus a inclus teorema în faimosul său „Caleidoscop matematic”. De atunci, teorema lui Pick a devenit cunoscută pe scară largă. În Germania, formula lui Pick este inclusă în manualele școlare.

Este un rezultat clasic al geometriei combinatorii și al geometriei numerelor.

Dovada formulei lui Pick

Fie ABCD un dreptunghi cu vârfuri la nodurile și laturile care rulează de-a lungul liniilor grilei (Anexa 3, Figura 3).

Să notăm cu B numărul de noduri aflate în interiorul dreptunghiului și cu G numărul de noduri de pe marginea acestuia. Să deplasăm grila o jumătate de celulă la dreapta și o jumătate de celulă

jos. Apoi, teritoriul dreptunghiului poate fi „distribuit” între noduri, după cum urmează: fiecare dintre nodurile B „controlează” o întreagă celulă a grilei deplasate, iar fiecare dintre nodurile G controlează 4 noduri non-colț de graniță - jumătate de celulă , iar fiecare dintre punctele de colț controlează un sfert de celulă. Prin urmare, aria dreptunghiului S este egală cu

S = B + + 4 · = B + - 1 .

Deci, pentru dreptunghiuri cu vârfuri la nodurile și laturile de-a lungul liniilor grilei, am stabilit formula S = B + - 1 . Aceasta este formula Peak.

Se pare că această formulă este valabilă nu numai pentru dreptunghiuri, ci și pentru poligoane arbitrare cu vârfuri la nodurile grilei.

Partea practică

Găsirea ariei figurilor folosind metoda geometrică și folosind formula Pick

Am decis să mă asigur că formula lui Pick este corectă pentru toate exemplele luate în considerare.

Se dovedește că, dacă un poligon poate fi tăiat în triunghiuri cu vârfuri la nodurile grilei, atunci formula lui Pick este adevărată pentru el.

M-am uitat la unele probleme pe hârtie în carouri cu pătrate de 1 cm1 cm și am realizat analiza comparativa privind rezolvarea problemelor (Tabelul nr. 1).

Tabelul nr. 1 Rezolvarea problemelor în diverse moduri.

Desen

Conform formulei de geometrie

Conform formulei lui Pick

Sarcina nr. 1

S=S etc -(2S 1 +2S 2 )

S etc =4*5=20 cm 2

S 1 =(2*1)/2=1 cm 2

S 2 =(2*4)/2=4 cm 2

S=20-(2*1+2*4)=10 cm 2

Răspuns :10 cm ².

B = 8, D = 6

S= 8 + 6/2 – 1 = 10 (cm²)

Răspuns: 10 cm².

Sarcina nr. 2

a=2, h=4

S=a*h=2*4=8 cm 2

Răspuns : 8 cm ².

B = 6, D = 6

S= 6 + 6/2 – 1 = 8 (cm²)

Răspuns: 8 cm².

Sarcina nr. 3

S=S kv -(S 1 +2S 2 )

S kv =4 2 =16 cm 2

S 1 =(3*3)/2=4,5cm 2

S 2 =(1*4)/2=2cm 2

S=16-(4,5+2*2)=7,5 cm2

B = 6, D = 5

S= 6 + 5/2 – 1 = 7,5 (cm²)

Răspuns: 7,5 cm².

Sarcina nr. 4

S=S etc -(S 1 +S 2+ S 3 )

S etc =4 * 3=12 cm 2

S 1 =(3*1)/2=1,5 cm 2

S 2 =(1*2)/2=1 cm 2

S 3 =(1+3)*1/2=2 cm 2

S=12-(1,5+1+2)=7,5 cm 2

B = 5, D = 7

S= 5 + 7/2 – 1 = 7,5 (cm²)

Răspuns: 7,5 cm².

Sarcina nr. 5.

S=S etc -(S 1 +S 2+ S 3 )

S etc =6 * 5=30 cm 2

S 1 =(2*5)/2=5 cm 2

S 2 =(1*6)/2=3 cm 2

S 3 =(4*4)/2=8 cm 2

S=30-(5+3+8)=14 cm 2

Răspuns: 14 cm²

B = 12, D = 6

S= 12 + 6/2 – 1 = 14 (cm²)

Răspuns: 14 cm²

Sarcină №6.

S tr =(4+9)/2*3=19,5 cm 2

Răspuns: 19,5 cm 2

H = 12, D = 17

S= 12 + 17/2 – 1 = 19,5 (cm²)

Răspuns: 19,5 cm 2

Sarcină №7. Găsiți aria pădurii (în m²) prezentată pe un plan cu o grilă pătrată de 1 × 1 (cm) pe o scară de 1 cm - 200 m

S= S 1 +S 2+ S 3

S 1 =(800*200)/2=80000 m 2

S 2 =(200*600)/2=60000 m 2

S 3 =(800+600)/2*400=

280000 m 2

S= 80000+60000+240000=

420000m2

Răspuns: 420.000 m²

B = 8, D = 7. S= 8 + 7/2 – 1 = 10,5 (cm²)

1 cm² - 200² m²; S= 40.000 10,5 = 420.000 (m²)

Răspuns: 420.000 m²

Problema nr. 8 . Găsiți aria câmpului (în m²) afișată pe un plan cu o grilă pătrată de 1 × 1 (cm) la scară

1 cm – 200 m.

S= S kv -2( S tr + S scară)

S sq =800 * 800 = 640000 m 2

S tr =(200*600)/2=60000m 2

S scara =(200+800)/2*200=

100000m2

S=640000-2(60000+10000)=

320000 m2

Răspuns: 320.000 m²

Soluţie. Sa gasim Saria unui patrulater desenat pe hârtie în carouri folosind formula lui Pick:S= B + - 1

B = 7, D = 4. S= 7 + 4/2 – 1 = 8 (cm²)

1 cm² - 200² m²; S= 40.000 8 = 320.000 (m²)

Răspuns: 320.000 m²

Problema nr. 9 . Găsiți zonaS sector, având în vedere laturile celulelor pătrate egale cu 1. În răspunsul dvs., indicați .

Un sector este un sfert dintr-un cerc și, prin urmare, aria lui este un sfert din aria cercului. Aria unui cerc este πR 2 , Unde R – raza cercului. În cazul nostruR =√5 si deci zonaS sectorul este 5π/4. UndeS/π=1,25.

Răspuns. 1.25.

Г= 5, В= 2, S= V + G/2 – 1= 2 + 5/2 – 1= 3,5, ≈ 1,11

Răspuns. 1.11.

Sarcina nr. 10. Găsiți zona S inele, considerând laturile celulelor pătrate egale cu 1. În răspunsul dvs., indicați .

Aria inelului este egală cu diferența dintre zonele cercului exterior și cel interior. RazăR cercul exterior este egal

2, raza r cercul interior este 2. Prin urmare, aria inelului este 4prin urmare. Răspuns: 4.

Г= 8, В= 8, S= V + G/2 – 1= 8 + 8/2 – 1=11, ≈ 3,5

Răspuns: 3.5

Concluzii: Sarcinile luate în considerare sunt similare sarcinii din opțiunile de control și măsurare Materiale pentru examenul de stat unificat la matematică (probleme nr. 5,6),.

Din soluțiile luate în considerare la probleme, am văzut că unele dintre ele, de exemplu problemele nr. 2.6, sunt mai ușor de rezolvat folosind formule geometrice, deoarece înălțimea și baza pot fi determinate din desen. Dar majoritatea sarcinilor necesită împărțirea figurii în altele mai simple (sarcina nr. 7) sau construirea ei într-un dreptunghi (sarcinile nr. 1,4,5), pătrat (sarcina nr. 3,8).

Din rezolvarea problemelor nr. 9 și nr. 10, am văzut că aplicarea formulei Pick la figuri care nu sunt poligoane dă un rezultat aproximativ.

Pentru a verifica raționalitatea utilizării formulei Peak, am realizat un studiu asupra timpului petrecut (Anexa 4, tabelul nr. 2).

Concluzie: din tabel și diagramă (Anexa 4, diagrama 1) reiese clar că la rezolvarea problemelor folosind formula Peak se petrece mult mai puțin timp.

Găsirea suprafeței formelor spațiale

Să verificăm aplicabilitatea acestei formule la forme spațiale (Anexa 5, Figura 4).

Găsiți zonă suprafata intreaga paralelipiped dreptunghiular, considerând laturile celulelor pătrate egale cu 1.

Acesta este un defect al formulei.

Aplicarea formulei lui Peak pentru a găsi zona unui teritoriu

Rezolvând probleme cu conținut practic (probleme nr. 7,8; tabelul nr. 1), am decis să folosesc această metodă pentru a găsi zona pe teritoriul școlii noastre, microdistrictele orașului Ust-Ilimsk , regiunea Irkutsk.

După ce m-am familiarizat cu „Proiectul limitelor terenului MAOUSOSH nr. 11 din Ust-Ilimsk” (Anexa 6), am găsit zona teritoriului școlii noastre și am comparat-o cu zona conform limitele de proiect ale terenului (Anexa 9, tabelul 3).

După ce am examinat harta părții malului drept al Ust-Ilimsk (Anexa 7), am calculat zonele microdistrictelor și le-am comparat cu datele din „Planul general al Ust-Ilimsk, Regiunea Irkutsk”. Rezultatele au fost prezentate în tabel (Anexa 9, Tabelul 4).

După ce am examinat harta regiunii Irkutsk (Anexa 7), am găsit zona teritoriului și am comparat-o cu datele de pe Wikipedia. Rezultatele au fost prezentate în tabel (Anexa 9, Tabelul 5).

După ce am analizat rezultatele, am ajuns la concluzia: folosind formula Peak, aceste zone pot fi găsite mult mai ușor, dar rezultatele sunt aproximative.

Din cercetările efectuate, am obținut cea mai precisă valoare la găsirea zonei teritoriului școlar (Anexa 10, Diagrama 2). O discrepanță mai mare a rezultatelor a fost obținută la găsirea zonei regiunii Irkutsk (Anexa 10, Diagrama 3). Acest lucru este legat de asta. Că nu toate limitele zonei sunt laturi ale poligoanelor, iar vârfurile nu sunt puncte de nod.

Concluzie

În urma muncii mele, mi-am extins cunoștințele despre rezolvarea problemelor pe hârtie în carouri și mi-am determinat clasificarea problemelor studiate.

În timpul lucrării, au fost rezolvate probleme pentru a găsi zona poligoanelor descrise pe hârtie în carouri în două moduri: geometric și folosind formula Pick.

Analiza soluțiilor și un experiment pentru a determina timpul petrecut au arătat că utilizarea formulei face posibilă rezolvarea problemelor de găsire a ariei unui poligon mai rațional. Acest lucru vă permite să economisiți timp la examenul de stat unificat la matematică.

Găsirea ariei diferitelor figuri descrise pe hârtie în carouri ne-a permis să concluzionam că utilizarea formulei Pick pentru a calcula aria unui sector circular și a unui inel este inadecvată, deoarece oferă un rezultat aproximativ și că formula Pick nu este folosit pentru a rezolva probleme în spațiu.

Lucrarea a găsit și zonele diferitelor teritorii folosind formula Peak. Putem concluziona: utilizarea formulei pentru a găsi aria diferitelor teritorii este posibilă, dar rezultatele sunt aproximative.

Ipoteza pe care am propus-o a fost confirmată.

Am ajuns la concluzia că tema care m-a interesat era destul de multifațetă, problemele de pe hârtie în carouri erau variate, iar metodele și tehnicile de rezolvare a acestora erau și ele variate. Prin urmare, am decis să continui să lucrez în această direcție.

Literatură

Volkov S.D.. Proiectul limitelor terenurilor, 2008, p. 16.

Gorina L.V., Matematică. Totul pentru profesor, M:Nauka, 2013. Nr. 3, p. 28.

Prokopyeva V.P., Petrov A.G., Planul general al orașului Ust-Ilimsk, regiunea Irkutsk, Gosstroy al Rusiei, 2004. p. 65.

Riess E. A., Zharkovskaya N. M., Geometria hârtiei în carouri. Formula lui Peak. - Moscova, 2009, nr. 17, p. 24-25.

Smirnova I. M. ,. Smirnov V. A. Geometrie pe hârtie în carouri. – Moscova, Chistye Prudy, 2009, p. 120.

Smirnova I. M., Smirnov V. A., Probleme geometrice cu conținut practic. – Moscova, Chistye Prudy, 2010, p. 150

Probleme ale bancului deschis de sarcini în matematică FIPI, 2015.

Harta orașului Ust-Ilimsk.

Harta regiunii Irkutsk.

Wikipedia.

Formula lui Pick

1. Introducere

2. Formula lui Peak. Anexa I.

Dovada II.

Dovada Sh.

3. Obiective.

4. Formula pentru aria unui poligon folosind coordonatele vârfurilor.

5. Sarcini.

6. Literatură

Formula lui Peak.

1. Introducere.

Extragem înțelepciune din istorie,

în poezie - inteligență,

în matematică – perspicacitate.

F. Bacon

Intriga se va desfășura pe o bucată obișnuită de hârtie în carouri.

Liniile care se desfășoară de-a lungul părților laterale ale celulelor formează o grilă, iar vârfurile celulelor sunt nodurile acestei grile. Să desenăm un poligon pe foaia cu vârfuri la noduri și să îi găsim aria.

Îl poți căuta în diferite moduri. De exemplu, puteți tăia un poligon în suficiente figuri simple, găsiți-le zonele și adăugați-le.

Dar aici ne așteaptă multe necazuri. Figura este ușor împărțită în dreptunghiuri, trapeze și triunghiuri, iar aria sa este calculată fără efort.

Deși poligonul pare destul de simplu, calcularea ariei sale necesită multă muncă. Dacă poligonul arăta mai elegant? Se dovedește că ariile poligoanelor ale căror vârfuri sunt situate la nodurile grilei pot fi calculate mult mai simplu: există o formulă care leagă aria lor de numărul de noduri situate în interiorul și la marginea poligonului. Această formulă minunată și simplă se numește formula Pick.

2. Formula lui Peak.

Vârfurile unui poligon (nu neapărat convexe) sunt situate la nodurile unei rețele întregi. În interiorul său se află B noduri de rețea, iar la graniță sunt G noduri. Să demonstrăm că aria sa este egală cu B + – 1 (Alegeți formula).

Anexa I.

Să considerăm un poligon ale cărui vârfuri sunt situate la nodurile unei rețele întregi, adică au coordonate întregi.

Împărțim poligonul în triunghiuri cu vârfuri la nodurile rețelei, care nu conțin noduri nici în interior, nici pe laturi.

Să notăm:

n- numărul de laturi ale poligonului,

m– numărul de triunghiuri cu vârfuri la nodurile rețelei care nu conțin noduri nici în interior, nici pe laturi,

B – numărul de noduri din interiorul poligonului,

Г – numărul de noduri de pe laturi, inclusiv vârfurile.

Arii tuturor acestor triunghiuri sunt aceleași și egale.

Prin urmare, aria poligonului este
.

180 0 m .

Acum să găsim această sumă într-un alt mod.

Suma unghiurilor cu un vârf la orice nod intern este 360 0.

Apoi, suma unghiurilor cu vârfuri la toate nodurile interne este egală cu 360 0 V.

Suma totală a unghiurilor pentru nodurile de pe laturi, dar nu de la vârfuri, este 180 0 (G - n).

Suma unghiurilor de la vârfurile poligonului este 180 0 ( n – 2) .

Suma totală a unghiurilor tuturor triunghiurilor este 360 0 V + 180 0 (G – n) + 180 0 (n – 2).

Deci 180 0 m= 360 0 V + 180 0 (G – n) + 180 0 (n – 2),

180 0 m= 360 0 V + 180 0 G – 180 0 n + 180 0 n– 180 0 2,

180 0 m= 360 0 V + 180 0 G – 360 0,

= B + – 1 ,

din care obținem expresia pentru aria S a poligonului:

S= B + – 1 ,

cunoscut sub numele de formula lui Pick.

În figură: B = 24, D = 9, prin urmare,S = 24 + – 1 = 27,5.

Să găsim aria primului poligon folosind formula lui Peak:

B = 28 (puncte verzi);

G = 20 (puncte albastre).

Obținem, S =
= 37 unități mp

Dovada II.

Fiecărui poligon M cu vârfuri la nodurile unei rețele întregi îi atribuim un număr f (M) =
, unde însumarea se efectuează peste toate nodurile rețelei aparținând lui M și unghiul este definită după cum urmează: =
pentru punctul interior al poligonului, =
pentru un punct de limită, altul decât un vârf, și – unghiul vârfului, dacă acest nod este un vârf. Este ușor de observat că f(M) =
+
= B + – 1. Rămâne de verificat dacă numărul f (M) este egal cu aria poligonului M.

Fie ca poligonul M să fie tăiat în poligoane M 1 și M 2 cu vârfuri la nodurile rețelei. Atunci f (M) = f (M 1) + f (M 2), deoarece pentru fiecare nod se adună unghiurile. Prin urmare, dacă formula lui Pick este adevărată pentru două dintre poligoane M, M 1 și M 2, atunci este adevărată și pentru al treilea.

Dacă M este un dreptunghi cu laturi pȘi q, îndreptată de-a lungul liniilor de zăbrele, apoi

f (M) = (p – 1)(q – 1) +
= pq.

În acest caz, formula lui Peak este valabilă. Tăiind un dreptunghi M cu diagonală în triunghiuri M 1 și M 2 și folosind faptul că f (M 1) = f (M 1) + f (M 2) și f (M 1) = f (M 2), se este ușor de demonstrat validitatea formulei Pick pentru orice triunghi dreptunghic cu catete îndreptate de-a lungul liniilor rețelei. Tăiind mai multe dintre aceste triunghiuri dintr-un dreptunghi, puteți obține orice triunghi.

Pentru a finaliza demonstrația formulei lui Pick, rămâne de reținut că orice poligon poate fi tăiat în triunghiuri prin diagonale disjunse.

Dovada Sh.

Relația dintre aria unei figuri și numărul de noduri incluse în această figură este vizibilă în mod deosebit în cazul unui dreptunghi.

Lăsa ABCD- un dreptunghi cu vârfuri la nodurile și laturile care rulează de-a lungul liniilor grilei.

Să notăm prin ÎN numărul de noduri situate în interiorul dreptunghiului și prin G- numărul de noduri de pe limita sa. Să mutăm grila o jumătate de celulă la dreapta și o jumătate de celulă în jos.

Apoi teritoriul dreptunghiului poate fi „distribuit” între noduri după cum urmează: fiecare dintre ÎN nodurile „controlează” o întreagă celulă a grilei deplasate, fiecare dintre G– 4 noduri de margine non-colț sunt jumătate de celulă, iar fiecare dintre punctele de colț este un sfert de celulă. Prin urmare, aria dreptunghiului S este egală cu

Deci, pentru dreptunghiuri cu vârfuri la noduri și laturi de-a lungul liniilor de grilă, am stabilit formula

Să demonstrăm că această formulă este adevărată nu numai pentru dreptunghiuri, ci și pentru poligoane arbitrare cu vârfuri la nodurile grilei.

Să notăm prin S m zona poligonuluiM cu vârfuri la noduri și prinP m - mărimea
, UndeÎN m – numărul de noduri în interiorM, A G m - numărul de noduri de la graniță. Atunci formula lui Peak poate fi scrisă ca
.

Vom împărți demonstrația formulei în mai multe etape.

Pasul 1.

Dacă poligonulM cu vârfuri la nodurile de plasă tăiate în 2 poligoaneM 1 Și M 2 , de asemenea, având vârfuri numai la nodurile grilei, atunci
. Lasă poligonulM tăiate în poligoaneM 1 Și M 2 cu vârfuri la noduri de un segment AB. Toate nodurile, cu excepția celor care cad pe segmentAB, aduce contribuții egale în partea stângă și dreaptă a formulei. Să considerăm nodurile situate pe segmentul AB.

Dacă un astfel de nod se află între A și B (de exemplu, C), atunci pentru un poligonM este intern și pentru poligoaneM 1 Și M 2 - la limita. Prin urmare contribuția sa laP m este egal cu 1, iar în fiecare dintre expresii
Și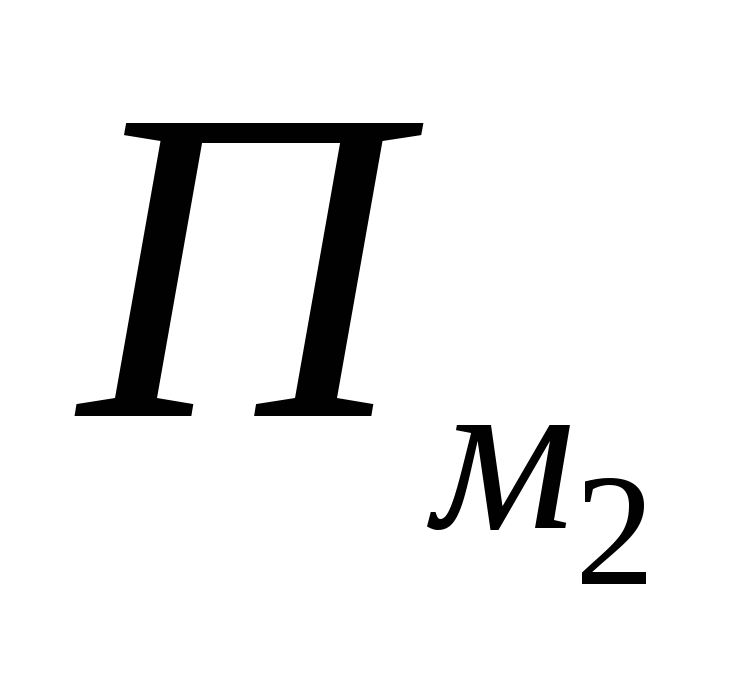
– 0,5 fiecare, adică contribuțiile unui astfel de nod laP m Și
sunt egale.

Să considerăm nodurile A și B. Sunt noduri de frontieră pentru ambele M, si pentru M 1 , M 2 .

Prin urmare, contribuția fiecăruia dintre aceste noduri laP m egal cu 0,5 a in
- unitate. Aceasta înseamnă că contribuția totală a nodurilor A și B laP m este egal cu 1, care este cu 1 mai mic decât contribuția lor la
. Dar
, A .

Din „contribuția” totală a tuturor nodurilor P m 1 se scade, iar din
2 se scade, iar aceasta compensează diferența dintre contribuțiile nodurilor A și B.

Asa de,
.

Pasul 2.

Dacă poligonul M cu vârfuri la nodurile de plasă tăiate în două poligoane M 1 Și M 2 (de asemenea, cu vârfuri la noduri) și formula este corectă pentru vreo două dintre poligoane MM 1 , M 2 , atunci este valabil și pentru al treilea poligon.

Să fie, de exemplu, adevărat pentruM 1 Și M 2 , acesta este
. Apoi (prin primul pas), dar pe primul pas) ultima expresie este egală cuP m , și egalitate
și există formula Peak.

Pasul 3.

Să demonstrăm formula lui Peak pentru un triunghi dreptunghic cu vârfuri la nodurile grilei și catetele situate pe liniile grilei.

Triunghi ABC construiește-l într-un dreptunghi ABCD .

Pentru dreptunghiuri, formula lui Pick este corectă: S ABCD = P ABCD . Conform primului pas P ABCD = P ABC + P ACD , P ABC = P ACD , Asa de P ABCD = 2P ABC . Dar S ABCD = 2 S ABC . De aceea S ABC = P ABC .

Pasul 4.

Formula lui Pick este valabilă pentru un triunghi arbitrar cu vârfuri la nodurile grilei.

După ce ați examinat figura, este ușor de înțeles: orice astfel de triunghi poate fi obținut prin „decuparea” dintr-un anumit dreptunghi cu laturile de-a lungul liniilor grilei, mai multe dreptunghiuri și triunghiuri dreptunghiulare cu picioare pe liniile grilei. Și deoarece formula lui Pick este adevărată pentru dreptunghiuri și triunghiuri dreptunghiulare, atunci (amintiți-vă de pasul 2) este valabilă și pentru triunghiul original.

Am demonstrat că, dacă un poligon poate fi tăiat în triunghiuri cu vârfuri la nodurile grilei, atunci formula lui Peak este adevărată pentru el.

3. Obiective.

Găsiți aria figurilor:

1
.