Raziskovalni projekt »Formula vrha v geometriji karirastega papirja. Formula vrha v šolskem tečaju planimetrije

Besedilo dela je postavljeno brez slik in formul.
Celotna različica dela je na voljo v zavihku "Delovne datoteke" v formatu PDF

Uvod

Sem učenka 6. razreda. Geometrijo sem začel študirati od lanskega leta, saj se v šoli učim po učbeniku »Matematika. Aritmetika. Geometrija "uredil Ye.A. Bunimovich, L.V. Kuznetsova, S.S. Minaeva in drugi.

Največ pozornosti so pritegnile teme "Kvadrati številk", "Risanje formul". Opazil sem, da je mogoče območja enakih oblik najti na različne načine. V vsakdanjem življenju se pogosto srečujemo z nalogami iskanja območja. Na primer, poiščite površino tal za barvanje. Zanimivo je, navsezadnje, da bi kupili potrebno količino ozadja za obnovo, morate poznati velikost sobe, t.j. območje stene. Izračunavanje površine kvadrata, pravokotnika in pravokotnega trikotnika je bilo zame preprosto.

Ko sem se začel zanimati za to temo, sem začel iskati dodatno gradivo na internetu. Kot rezultat iskanja sem naletel na Pickovo formulo - to je formula za izračun površine mnogokotnika, narisanega na karirasti papir. Izračun površine po tej formuli se mi je zdel dostopen vsakemu študentu. Zato sem se odločil za raziskovalno delo.

Relevantnost teme:

Ta tema je dopolnitev in poglobitev študija predmeta geometrija.

Preučevanje te teme vam bo pomagalo, da se bolje pripravite na olimpijade in izpite.

Cilj:

Oglejte si Pickovo formulo.

Obvladajte tehnike reševanja geometrijskih problemov s formulo Pick.

Sistematizirati in povzeti teoretično in praktično gradivo.

Cilji raziskave:

Preverite učinkovitost in izvedljivost uporabe formule pri reševanju problemov.

Naučite se uporabljati formulo Peak pri težavah različne kompleksnosti.

Primerjajte težave, rešene s formulo Pick, in tradicionalno metodo.

Glavni del

1.1. Sklic na zgodovino

Georg Alexander Pick je avstrijski matematik, rojen 10. avgusta 1859. Bil je nadarjen otrok, poučeval ga je oče, ki je vodil zasebni inštitut. Georg je pri 16 letih končal srednjo šolo in se vpisal na univerzo na Dunaju. Pri 20 letih je dobil pravico do poučevanja fizike in matematike. Formula za določanje površine mreže poligonov mu je prinesla svetovno slavo. Svojo formulo je objavil v članku leta 1899. Postala je priljubljena, ko jo je poljski znanstvenik Hugo Steinhaus leta 1969 vključil v objavo matematičnih fotografij.

Georg Pick se je izobraževal na Univerzi na Dunaju in leta 1880 zagovarjal doktorat. Po doktoratu je bil imenovan za asistenta Ernesta Macha na univerzi Sherl-Ferdinand v Pragi. Tam je postal tudi učitelj. V Pragi je ostal do upokojitve leta 1927 in se nato vrnil na Dunaj.

Pick je vodil odbor na nemški univerzi v Pragi, ki je leta 1911 imenoval Einsteina za profesorja na oddelku za matematično fiziko.

Izvoljen je bil za člana Češke akademije znanosti in umetnosti, a so ga po nacističnem zavzetju Prage izključili.

Ko so 12. marca 1938 nacisti vstopili v Avstrijo, se je vrnil v Prago. Marca 1939 so nacisti napadli Češkoslovaško. 13. julija 1942 je bil Peak deportiran v taborišče Theresienstadt, ki so ga ustanovili nacisti v severni Češki, kjer je umrl dva tedna pozneje v starosti 82 let.

1.2. Raziskave in dokazi

Svoje raziskovalno delo sem začel z razjasnitvijo vprašanja: področja katerih številk lahko najdem? Lahko bi pripravil formulo za izračun površine različnih trikotnikov in štirikotnikov. Kaj pa pet, šest in na splošno s poligoni?

Med raziskovanjem na različnih mestih sem videl rešitve problemov za izračun površine petih, šestih in drugih poligonov. Formula za reševanje teh problemov se je imenovala Pickova formula. Izgleda takole: S = B + G / 2-1, kje V- število vozlišč, ki ležijo znotraj poligona, G- število vozlišč, ki ležijo na meji poligona. Posebnost te formule je, da se lahko uporablja samo za poligone, narisane na karirasti papir.

Vsak tak mnogokotnik zlahka razdelimo na trikotnike z oglišči na vozliščih rešetke, ki ne vsebujejo vozlišč niti znotraj niti na straneh. Lahko se pokaže, da so površine vseh teh trikotnikov enake in enake ½, zato je površina mnogokotnika polovica njihovega števila T.

Da bi našli to število, z n označimo število stranic mnogokotnika z V- število vozlišč znotraj njega, skozi G- število vozlišč na straneh, vključno z oglišči. Skupna vsota kotov vseh trikotnikov je 180 °. T.

Zdaj pa poiščimo vsoto na drugačen način.

Vsota kotov z vrhom na katerem koli notranjem vozlišču je 2,180 °, t.j. skupni koti so 360°. V; skupna vsota kotov pri vozliščih na straneh, ne pa na ogliščih, je ( G-n) 180° in vsota kotov na ogliščih mnogokotnika bo ( G-2) 180°. V to smer, T = 2.180 °. B + (G-n) 180° + (n -2)180 °. Po razširitvi oklepajev in delitvi za 360 ° dobimo formulo za površino S poligona, znano kot Pickova formula.

2. Praktični del

Odločil sem se, da to formulo preverim pri nalogah iz zbirke OGE-2017. Vzela sem naloge za izračun površine trikotnika, štirikotnika in petkotnika. Odločil sem se primerjati odgovore in rešiti na dva načina: 1) v pravokotnik sem dodal figure in od površine nastalega pravokotnika odštel površino pravokotnih trikotnikov; 2) uporabili Pickovo formulo.

S = 18-1,5-4,5 = 12 in S = 7 + 12 / 2-1 = 12

S = 24-9-3 = 12 in S = 7 + 12 / 2-1 = 12

S = 77-7,5-12-4,5-4 = 49 in S = 43 + 14 / 2-1 = 49

Če primerjam prejete, sklepam, da obe formuli dajeta enak odgovor. Iskanje površine figure s formulo Peak se je izkazalo za hitrejše in lažje, saj je bilo manj izračunov. Enostavnost rešitve in prihranek časa pri izračunih mi bosta v prihodnje koristila pri opravljanju OGE.

To me je spodbudilo, da sem preizkusil možnost uporabe Pickove formule na bolj zapletenih oblikah.

S = 0 + 4/2 -1 = 1

S = 5 + 11 / 2-1 = 9,5

S = 4 + 16 / 2-1 = 1

Zaključek

Peakova formula je enostavna za razumevanje in enostavna za uporabo. Najprej je dovolj, da znaš šteti, deliti z 2, seštevati in odštevati. Drugič, lahko najdete območje in zapleteno obliko, ne da bi porabili veliko časa. Tretjič, ta formula deluje za kateri koli poligon.

Pomanjkljivost je, da je Pick Formula uporabna samo za oblike, ki so narisane na kockasti papir, oglišča pa ležijo na vozliščih celic.

Prepričan sem, da pri opravljanju končnih izpitov težave pri izračunu površine številk ne bodo povzročale težav. Navsezadnje Pickovo formulo že poznam.

Bibliografija

Bunimovič E.A., Dorofejev G.V., Suvorova S.B. in druga matematika. Aritmetika. Geometrija. 5. razred: izobraževalni. za splošno izobraževanje. organizacije s prid. na elektron. nosilec-3. izd.-M .: Izobraževanje, 2014.- 223, str. : bolna. - (Sfere).

Bunimovich E.A., Kuznetsova L.V., Minaeva S.S. in druga matematika. Aritmetika. Geometrija. 6. razred: vzgojno. za splošno izobraževanje. organizacije-5. izd.-M .: Izobraževanje, 2016.-240s. : ilustr. - (Sfere).

Vasiliev N.B. Okoli Pickove formule. // Kvant. - 1974.-№2. -s. 39-43

Rassolov V.V. Planimetrične naloge. / 5. izd., Rev. In dodaj. - M .: 2006.-640s.

I.V. Jaščenko, OGE. Matematika: tipične izpitne možnosti: O-39 36 možnosti - M .: Založba Narodna prosveta, 2017. -240 str. - (OGE. FIPI-šola).

"Rešil bom OGE": matematika. Sistem usposabljanja Dmitrija Guščina. OGE-2017: naloge, odgovori, rešitve [Elektronski vir]. Način dostopa: https://oge.sdamgia.ru/test?id=6846966 (datum zdravljenja 2.4.2017)

S formulo Pick lahko najdete površino figure, zgrajene na listu v celici (trikotnik, kvadrat, trapez, pravokotnik, mnogokotnik).

V nalogah, ki bodo na izpitu, je cela skupina nalog, v katerih je podan poligon, zgrajen na listu v celici in vprašanje je iskanje območja. Merilo celice je en kvadratni centimeter.

Oglejte si vsebino predstavitve

Georg Peak

Georg Alexander Peak,

avstrijski matematik

(10.08.1859 - 13.07.1942)

Formula je bila odkrita leta 1899.

Območje zahtevane številke lahko najdete po formuli:

M je število vozlišč na meji trikotnika (na straneh in ogliščih):
N je število vozlišč znotraj trikotnika;

* Z "vozlišči" mislimo na presečišče črt.

Najdimo površino trikotnika:

Označimo vozlišča:

1 celica = 1 cm

M = 15 (označeno z rdečo)
N = 34 (označeno z modro)

Poiščite površino paralelograma:

Označimo vozlišča:

M = 18 (označeno z rdečo)
N = 20 (označeno z modro)

Poiščimo površino trapeza:

Označimo vozlišča:

M = 24 (označeno z rdečo)
N = 25 (označeno z modro)

Poiščite površino mnogokotnika:

Označimo vozlišča:

M = 14 (označeno z rdečo)
N = 43 (označeno z modro)

Označimo vozlišča:

M = 11 (označeno z rdečo)
N = 5 (označeno z modro)

Odločite se sami:

1. Poišči površino štirikotnika, ki je upodobljen na karirastem papirju z velikostjo celice 1 cm x 1 cm. Odgovor napiši v kvadratnih centimetrih.

4. Poiščite površino štirikotnika, upodobljenega na karirastem papirju z velikostjo celice 1 cm x 1 cm. Odgovor navedite v kvadratnih centimetrih .

Opišimo pravokotnik blizu njega:

Od površine pravokotnika (v tem primeru je kvadrat) odštejemo površine nastalih preprostih številk:

odgovori:

№ naloge

1. možnost

2. možnost

3. možnost

4. možnost

Vrhunska formula

Sazhina Valeria Andreevna, učenec 9. razreda, MAOU "Srednja šola št. 11" Ust-Ilimsk, regija Irkutsk

Nadzornik: Gubar Oksana Mikhailovna, učitelj matematike najvišje kvalifikacijske kategorije MAOU "Srednja šola št. 11" Ust-Ilimsk, regija Irkutsk

2016 leto

Uvod

Med preučevanjem teme geometrije "Območja poligonov" sem se odločil ugotoviti: ali obstaja način, kako najti področja, ki se razlikujejo od tistih, ki smo jih preučevali v lekciji?

Ta način je formula Peak. L. V. Gorina je v »Gradivu za samoizobraževanje študentov« to formulo opisala takole: »Spoznavanje Pickove formule je še posebej pomembno na predvečer USE in Državne izpitne agencije. S to formulo lahko enostavno rešite velik razred problemov, ki jih ponujajo izpiti - to so težave pri iskanju površine mnogokotnika, upodobljenega na karirastem papirju. Pickova mala formula bo nadomestila celoten nabor formul, potrebnih za reševanje takšnih problemov. Pickova formula bo delovala "en za vse ..."! ".

V gradivu za izpit sem naletel na težave s praktičnimi vsebinami pri iskanju površine zemljiških parcel. Odločil sem se preveriti, ali je ta formula uporabna za iskanje območja šolskega ozemlja, mestnih mikrookrožij in regije. In tudi, ali ga je racionalno uporabiti za reševanje problemov.

Predmet raziskave: Peakova formula.

Predmet raziskave: racionalnost uporabe Pickove formule pri reševanju problemov.

Namen dela: utemeljiti racionalnost uporabe formule Pick pri reševanju problemov iskanja površine figur, upodobljenih na karirastem papirju.

Raziskovalne metode: modeliranje, primerjava, posploševanje, analogije, preučevanje literarnih in internetnih virov, analiza in klasifikacija informacij.

Izberite potrebno literaturo, analizirajte in sistematizirajte prejete informacije;

Razmislite o različnih metodah in tehnikah za reševanje problemov na karirastem papirju;

Eksperimentalno preverite racionalnost uporabe formule Pick;

Razmislite o uporabi te formule.

Hipoteza: če za iskanje površin poligona uporabite formulo Peak, potem lahko najdete površino ozemlja in reševanje problemov na karirastem papirju bo bolj racionalno.

Glavni del

Teoretični del

Karirasti papir (natančneje njegova vozlišča), na katerega pogosto raje rišemo in rišemo, je eden najpomembnejših primerov pikčaste rešetke na ravnini. Že ta preprosta mreža je služila kot izhodišče za K. Gaussa za primerjavo površine kroga s številom točk s celimi koordinatami, ki se nahajajo znotraj njega. Dejstvo, da imajo nekatere preproste geometrijske trditve o figurah na ravnini globoke posledice v aritmetičnih študijah, je izrecno opozoril G. Minkowski leta 1896, ko je prvič uporabil geometrijske metode za obravnavanje teoretsko-teoretičnih problemov.

Na kariran papir narišemo poligon (Priloga 1, slika 1). Poskusimo zdaj izračunati njegovo površino. Kako narediti? Verjetno ga je najlažje razdeliti na pravokotne trikotnike in trapez, katerih površine je že enostavno izračunati in rezultate sešteti.

Uporabljena metoda je preprosta, vendar zelo okorna, poleg tega pa ni primerna za vse poligone. Naslednjega mnogokotnika torej ni mogoče razdeliti na pravokotne trikotnike, kot smo to storili v prejšnjem primeru (Dodatek 2, slika 2). Lahko ga na primer poskusite dopolniti z "dobrim", ki ga potrebujemo, torej s tistim, za katerega lahko izračunamo površino, ki jo lahko izračunamo na opisan način, nato odštejemo površine dodanih delov iz nastalega števila.

Vendar se izkaže, da obstaja zelo preprosta formula, ki vam omogoča izračun površin takšnih poligonov z oglišči na vozliščih kvadratne mreže.

To formulo je leta 1899 odkril avstrijski matematik Pik Georg Aleksandrov (1859 - 1943). Poleg te formule je Georg Pieck odkril izreke Pieck, Pieck - Julia, Pieck - Nevalina in dokazal neenakost Schwarz - Pieck.

Ta formula je bila nekaj časa neopažena po tem, ko jo je Peek objavil, vendar je poljski matematik Hugo Steinhaus leta 1949 vključil izrek v svoj slavni matematični kalejdoskop. Od takrat naprej je Pickov izrek postal splošno znan. V Nemčiji je Pickova formula vključena v šolske učbenike.

Je klasičen rezultat kombinatorne geometrije in geometrije števil.

Dokaz o Pickovi formuli

Naj bo ABCD pravokotnik z oglišči na vozliščih in stranicah vzdolž mrežnih črt (Dodatek 3, slika 3).

Označimo z В - število vozlišč, ki ležijo znotraj pravokotnika, in z Г - število vozlišč na njegovi meji. Premaknite mrežo za polovico celice v desno in za polovico celice

dol. Nato se lahko ozemlje pravokotnika "razporedi" med vozlišča na naslednji način: vsako od vozlišč B "nadzoruje" celotno celico premaknjene mreže in vsako od vozlišč G - 4 mejna vozlišča brez kotov - polovico celice , in vsaka od vogalnih točk - četrtina celice. Zato je površina pravokotnika S enaka

S = B + + 4 = B + - 1 .

Torej, za pravokotnike z oglišči na vozliščih in straneh, ki potekajo vzdolž mrežnih črt, nastavimo formulo S = B + - 1 . To je Pickova formula.

Izkazalo se je, da ta formula ne velja samo za pravokotnike, ampak tudi za poljubne mnogokotnike z oglišči na vozliščih mreže.

Praktični del

Iskanje površine figur z geometrijsko metodo in s formulo Pick

Odločil sem se, da se prepričam, da je Pickova formula pravilna za vse primere, ki sem si jih ogledal.

Izkazalo se je, da če lahko poligon razrežemo na trikotnike z oglišči na vozliščih mreže, potem zanj velja Pickova formula.

Pregledala sem nekaj nalog na karirastem papirju s celicami velikosti 1 cm1 cm in opravila primerjalno analizo za reševanje nalog (tabela 1).

Tabela №1 Reševanje problemov na različne načine.

Risanje

Po geometrijski formuli

Po formuli Peak

Problem številka 1

S = S itd - (2S 1 + 2S 2 )

S itd =4*5=20 cm 2

S 1 =(2*1)/2=1 cm 2

S 2 =(2*4)/2=4 cm 2

S = 20- (2 * 1 + 2 * 4) = 10 cm 2

Odgovori :10 cm ².

B = 8, G = 6

S= 8 + 6/2 - 1 = 10 (cm²)

Odgovor: 10 cm².

Problem številka 2

a = 2, h = 4

S = a * h = 2 * 4 = 8 cm 2

Odgovori : 8 cm ².

B = 6, G = 6

S= 6 + 6/2 - 1 = 8 (cm²)

Odgovor: 8 cm².

Problem številka 3

S = S sq. - (S 1 + 2S 2 )

S sq. =4 2 =16 cm 2

S 1 = (3 * 3) / 2 = 4,5 cm 2

S 2 = (1 * 4) / 2 = 2 cm 2

S= 16- (4,5 + 2 * 2) = 7,5 cm 2

B = 6, G = 5

S= 6 + 5/2 - 1 = 7,5 (cm²)

Odgovor: 7,5 cm².

Problem številka 4

S = S itd - (S 1 + S 2+ S 3 )

S itd =4 * 3=12 cm 2

S 1 =(3*1)/2=1,5 cm 2

S 2 =(1*2)/2=1 cm 2

S 3 =(1+3)*1/2=2 cm 2

S = 12- (1,5 + 1 + 2) = 7,5 cm 2

B = 5, G = 7

S= 5 + 7/2 - 1 = 7,5 (cm²)

Odgovor: 7,5 cm².

Problem št. 5.

S = S itd - (S 1 + S 2+ S 3 )

S itd =6 * 5=30 cm 2

S 1 =(2*5)/2=5 cm 2

S 2 =(1*6)/2=3 cm 2

S 3 =(4*4)/2=8 cm 2

S = 30- (5 + 3 + 8) = 14 cm 2

Odgovor: 14 cm²

H = 12, G = 6

S= 12 + 6/2 - 1 = 14 (cm²)

Odgovor: 14 cm²

Naloga №6.

S tr = (4 + 9) / 2 * 3 = 19,5 cm 2

Odgovor: 19,5 cm 2

H = 12, G = 17

S= 12 + 17/2 - 1 = 19,5 (cm²)

Odgovor: 19,5 cm 2

Naloga №7. Poiščite površino gozda (v m²), prikazano na načrtu s kvadratno mrežo 1 × 1 (cm) v merilu 1 cm - 200 m

S = S 1 + S 2+ S 3

S 1 =(800*200)/2=80000 m 2

S 2 =(200*600)/2=60000 m 2

S 3 =(800+600)/2*400=

280000 m 2

S = 80000+60000+240000=

420000 m 2

Odgovor: 420.000 m²

B = 8, G = 7. S= 8 + 7/2 - 1 = 10,5 (cm²)

1 cm² - 200² m²; S= 40.000 10,5 = 420.000 (m2)

Odgovor: 420.000 m²

Problem številka 8 ... Poiščite površino polja (v m²), ki je prikazana na načrtu s kvadratno mrežo 1 × 1 (cm) v merilu

1 cm - 200 m.

S= S kvadratni -2 ( S tr + S lestev)

S m² = 800 * 800 = 640.000 m 2

S tr = (200 * 600) / 2 = 60000 m 2

S lestev = (200 + 800) / 2 * 200 =

100000 m 2

S=640000-2(60000+10000)=

320.000 m 2

Odgovor: 320.000 m²

Rešitev. Najti Spovršina štirikotnika, upodobljena na karirastem papirju z uporabo Pickove formule:S= B + - 1

B = 7, G = 4. S= 7 + 4/2 - 1 = 8 (cm²)

1 cm² - 200² m²; S= 40.000 8 = 320.000 (m2)

Odgovor: 320.000 m²

Problem številka 9 ... Poiščite območjeS sektorju, ob upoštevanju stranic kvadratnih celic enake 1. V odgovoru navedite .

Sektor je ena četrtina kroga, zato je njegova površina enaka četrtini površine kroga. Površina kroga je πR 2 , kje R Je polmer kroga. V našem primeruR =√5 in torej območjeS sektor je 5π / 4. KjeS/ π = 1,25.

Odgovori. 1.25.

G = 5, B = 2, S= B + G / 2 - 1 = 2 + 5/2 - 1 = 3,5, ≈ 1,11

Odgovori. 1.11.

Problem številka 10. Poiščite območje S obroče, ki štejejo stranice kvadratnih celic enake 1. V odgovoru navedite .

Površina obroča je enaka razliki med površinami zunanjega in notranjega kroga. polmerR zunanji krog je

2, polmer r notranji krog je 2. Zato je površina obroča 4in zato... Odgovor: 4.

G = 8, B = 8, S= B + G / 2 - 1 = 8 + 8/2 - 1 = 11, ≈ 3,5

Odgovor: 3.5

Zaključki: Obravnavane naloge so podobne nalogi iz možnosti za kontrolno-merno gradivo izpita iz matematike (naloge št. 5,6).

Iz obravnavanih rešitev nalog sem videl, da je nekatere od njih, na primer naloge št. 2.6, lažje rešiti z geometrijskimi formulami, saj je višino in osnovo mogoče določiti iz slike. Toda pri večini nalog je potrebno figuro razdeliti na enostavnejše (naloga št. 7) ali dokončati konstrukcijo na pravokotnik (naloge št. 1,4,5), kvadrat (naloge št. 3,8).

Pri reševanju problemov #9 in #10 sem videl, da uporaba Pickove formule za oblike, ki niso mnogokotniki, daje približen rezultat.

Da bi preveril racionalnost formule Peak, sem opravil študijo na temo porabljenega časa (Dodatek 4, tabela №2).

Zaključek: iz tabele in diagrama (Dodatek 4, diagram 1) je razvidno, da se pri reševanju problemov s formulo Peak porabi veliko manj časa.

Iskanje površine prostorskih oblik

Preverimo uporabnost te formule za prostorske oblike (Priloga 5, slika 4).

Poiščite skupno površino pravokotnega paralelepipeda, ob predpostavki, da so stranice kvadratnih celic enake 1.

To je napaka v formuli.

Uporaba formule Peak za iskanje površine ozemlja

Reševanje težav s praktičnimi vsebinami (naloge št. 7,8; tabela št. 1) sem se odločil uporabiti to metodo za iskanje območja ozemlja naše šole, mikrookrožij mesta Ust-Ilimsk , regija Irkutsk.

Po pregledu "Projekta meja zemljiške parcele MAUSOSH št. 11 v Ust-Ilimsku" (Dodatek 6) sem našel območje ozemlja naše šole in ga primerjal z območjem po osnutku meja zemljiško parcelo (Priloga 9, tabela 3).

Po pregledu zemljevida desnega obrežnega dela Ust-Ilimska (Priloga 7) sem izračunal površine mikrookrožij in jih primerjal s podatki iz "Splošnega načrta Ust-Ilimsk, Irkutska regija". Rezultati so predstavljeni v tabeli (Priloga 9, tabela 4).

Ko sem pregledal zemljevid regije Irkutsk (Dodatek 7), sem našel območje ozemlja in ga primerjal s podatki iz Wikipedije. Rezultati so predstavljeni v tabeli (Priloga 9, tabela 5).

Po analizi rezultatov sem prišel do zaključka: z uporabo formule Peak je mogoče ta področja najti veliko lažje, vendar so rezultati približni.

Iz opravljene raziskave sem dobil najbolj natančno vrednost pri iskanju površine šolskega ozemlja (Priloga 10, diagram 2). Večje neskladje v rezultatih je bilo doseženo pri iskanju območja Irkutske regije (Dodatek 10, diagram 3). To je posledica dejstva. Da niso vse meje območij stranice poligonov, oglišča pa niso sidrne točke.

Zaključek

Kot rezultat svojega dela sem razširil svoje znanje reševanja nalog na kariran papir, si določil klasifikacijo preučenih problemov.

Pri izvajanju dela so bile rešene težave z iskanjem površine poligonov, upodobljenih na karirastem papirju, na dva načina: geometrijsko in z uporabo formule Pick.

Analiza rešitev in eksperiment za določitev porabljenega časa sta pokazala, da uporaba formule omogoča reševanje problemov za iskanje površine poligona na bolj racionalen način. To prihrani čas na izpitu iz matematike.

Iskanje površine različnih figur, upodobljenih na karirastem papirju, je omogočilo sklepanje, da je uporaba Pickove formule za izračun površine krožnega sektorja in obroča nepraktična, saj daje približen rezultat in da je Pickova formula se ne uporablja za reševanje problemov v vesolju.

Tudi pri delu so bila s formulo Peak najdena območja različnih ozemelj. Sklepamo lahko, da je uporaba formule za iskanje območja različnih ozemelj možna, vendar so rezultati približni.

Hipoteza, ki sem jo postavil, je bila potrjena.

Prišel sem do zaključka, da je tema, ki me zanima, precej večplastna, naloge na karirastem papirju so raznolike, raznolike so tudi metode in tehnike za njihovo reševanje. Zato sem se odločil nadaljevati delo v tej smeri.

Literatura

Volkov SD .. Osnutek mej zemljiške parcele, 2008, str. šestnajst.

Gorina L.V., Matematika. Vse za učitelja, M: Nauka, 2013, št.3, str. 28.

Prokopyeva V.P., Petrov A.G., Splošni načrt mesta Ust-Ilimsk, regija Irkutsk, Gosstroy Rusije, 2004 str. 65.

Riss E.A., Zharkovskaya N.M., Geometrija karirastega papirja. Pickova formula. - Moskva, 2009, št. 17, str. 24-25.

Smirnova I. M.,. Smirnov V. A, Geometrija na karirastem papirju. - Moskva, Chistye Prudy, 2009, str. 120.

Smirnova I.M., Smirnov V.A., Geometrijski problemi s praktično vsebino. - Moskva, Chistye Prudy, 2010, str. 150

Problemi odprte banke nalog iz matematike FIPI, 2015.

Zemljevid mesta Ust-Ilimsk.

Zemljevid regije Irkutsk.

Wikipedia.

Vrhunska formula

1. Uvod

2. Pickova formula. Dokaz I.

Dokaz II.

Dokaz Sh.

3. Naloge.

4. Formula za površino poligona skozi koordinate oglišč.

5. Naloge.

6. Literatura

Pickova formula.

1. Uvod.

Iz zgodovine črpamo modrost,

v poeziji - duhovitost,

v matematiki, razsodnost.

F. Slanina

Zaplet se bo odvijal na navadnem kos karirastega papirja.

Črte, ki potekajo ob straneh celic, tvorijo mrežo, oglišča celic pa vozlišča te mreže. Na list narišemo poligon z oglišči na vozliščih in poiščemo njegovo površino.

Iščete ga lahko na različne načine. Poligon lahko na primer razrežete v dokaj preproste oblike, poiščete njihova območja in jih zložite.

Toda tukaj nas čaka veliko težav. Številko je mogoče zlahka razdeliti na pravokotnike, trapeze in trikotnike, njeno površino pa enostavno izračunamo.

Čeprav je poligon videti dovolj preprost, bo izračun njegove površine zahteval veliko dela. Kaj pa, če bi bil poligon videti bolj bizaren? Izkazalo se je, da je površine poligonov, katerih oglišča se nahajajo na vozliščih mreže, veliko lažje izračunati: obstaja formula, ki povezuje njihovo območje s številom vozlišč, ki ležijo znotraj in na meji poligona. Ta čudovita in preprosta formula se imenuje Pickova formula.

2. Pickova formula.

Vozlišča mnogokotnika (ni nujno konveksna) se nahajajo na vozliščih celoštevilske mreže. Znotraj nje leži B vozlišča mreže, na meji Γ pa vozlišč. Dokažimo, da je njegova površina enaka B + - 1 (Pickova formula).

Dokaz I.

Razmislite o poligonu, katerega oglišča so na vozliščih cele mreže, to pomeni, da imajo cele koordinate.

Poligon razdelite na trikotnike z oglišči na vozliščih rešetke, ki ne vsebujejo vozlišč niti znotraj niti na straneh.

Označimo:

n- število stranic mnogokotnika,

m- število trikotnikov z oglišči na vozliščih rešetke, ki ne vsebujejo vozlišč niti znotraj niti na straneh,

B - število vozlišč znotraj poligona,

Г je število vozlišč na straneh, vključno z oglišči.

Površine vseh teh trikotnikov so enake in enake.

Torej je površina poligona
.

180 0 m .

Zdaj pa poiščimo ta znesek na drugačen način.

Vsota kotov z vrhom na katerem koli notranjem vozlišču je 360 0.

Potem je vsota kotov z oglišči na vseh notranjih vozliščih 360 0 V.

Skupna vsota kotov na vozliščih na straneh, ne pa na ogliščih, je enaka 180 0 (Г - n).

Vsota kotov na ogliščih mnogokotnika je 180 0 ( n – 2) .

Skupna vsota kotov vseh trikotnikov je 360 0 V + 180 0 (G - n) + 180 0 (n – 2).

Torej 180 0 m= 360 0 V + 180 0 (G - n) + 180 0 (n – 2),

180 0 m= 360 0 V + 180 0 G - 180 0 n + 180 0 n- 180 0 2,

180 0 m= 360 0 V + 180 0 G - 360 0,

= B + – 1 ,

od koder dobimo izraz za površino S poligona:

S= B + – 1 ,

znana kot Pickova formula.

Na sliki: H = 24, G = 9, torejS = 24 + – 1 = 27,5.

Poiščite površino prvega mnogokotnika s formulo Pick:

B = 28 (zelene pike);

G = 20 (modre pike).

Dobimo, S =
= 37 kvadratnih enot

Dokaz II.

Vsakemu poligonu M z oglišči na vozliščih cele mreže dodelimo številko f (M) =
, kjer se seštevanje izvede po vseh mrežnih vozliščih, ki pripadajo M, in kotu je opredeljen kot sledi: =
za notranjo točko poligona, =
za mejno točko, ki ni točko, in - kot pri točki, če je dano vozlišče oglišče. Lahko je videti, da je f (M) =
+
= B + - 1. Ostaja preveriti, ali je število f (M) enako površini mnogokotnika M.

Naj bo mnogokotnik M razrezan na mnogokotnika M 1 in M 2 z oglišči na vozliščih mreže. Potem je f (M) = f (M 1) + f (M 2), saj se koti seštejejo za vsako vozlišče. Če torej Pickova formula velja za dva poligona M, M 1 in M 2, potem velja tudi za tretjega.

Če je M pravokotnik s stranicami str in q usmerjeno vzdolž mrežnih linij, nato

f (M) = (p - 1) (q - 1) +
= pq.

V tem primeru je Pickova formula veljavna. Pravokotnik M z diagonalo razrežemo na trikotnike M 1 in M 2 in uporabimo dejstvo, da je f (M) = f (M 1) + f (M 2) in f (M 1) = f (M 2), je enostavno dokazati Pick formulo za kateri koli pravokoten trikotnik z nogami, usmerjenimi vzdolž mrežnih linij. Če iz pravokotnika odrežete več teh trikotnikov, lahko dobite kateri koli trikotnik.

Za dokončanje dokaza Pickove formule je še treba omeniti, da je vsak mnogokotnik mogoče razrezati v trikotnike z disjunktivnimi diagonalami.

Dokaz Sh.

Razmerje med površino oblike in številom vozlišč, ki sodijo v to obliko, je še posebej jasno v primeru pravokotnika.

Pustiti ABCD- pravokotnik z oglišči na vozliščih in straneh vzdolž mrežnih linij.

Označimo z Vštevilo vozlišč, ki ležijo znotraj pravokotnika, in po G- število vozlišč na njegovi meji. Premaknite mrežo za polovico celice v desno in za polovico celice navzdol.

Nato se lahko ozemlje pravokotnika "razporedi" med vozlišča na naslednji način: vsako od V vozlišča "nadzoruje" celotno celico premaknjene mreže, vsako od G- 4 mejna nevogalna vozlišča - polovica celice in vsaka kotna točka - četrtina celice. Zato je površina pravokotnika S enaka

Torej, za pravokotnike z oglišči na vozliščih in straneh, ki potekajo vzdolž mrežnih črt, nastavimo formulo

Dokažimo, da ta formula ne velja samo za pravokotnike, ampak tudi za poljubne mnogokotnike z oglišči na vozliščih mreže.

Označimo z S m območje poligonaM z oglišči na vozliščih in skoziP m - vrednost
, kjeV m - število vozlišč v notranjostiM, a G m - število vozlišč na meji. Potem lahko Pickovo formulo zapišemo kot
.

Dokaz formule smo razdelili na več korakov.

Korak 1.

Če je poligonM z oglišči na mrežnih točkah je razrezana na 2 mnogokotnikaM 1 in M 2 , imajo tudi oglišča samo na vozliščih mreže
... Naj poligonM razrezan na poligoneM 1 in M 2 z oglišči na vozliščih po segmentih AB. Vsa vozlišča, razen tistih, ki spadajo na segmentAB, daje enak prispevek levi in desni strani formule. Razmislite o vozliščih, ki ležijo na segmentu AB.

Če takšno vozlišče leži med A in B (na primer C), potem za mnogokotnikM je notranji, vendar za poligoneM 1 in M 2 - meja. Zato je njegov prispevek kP m je enak 1 in v vsakem od izrazov
in
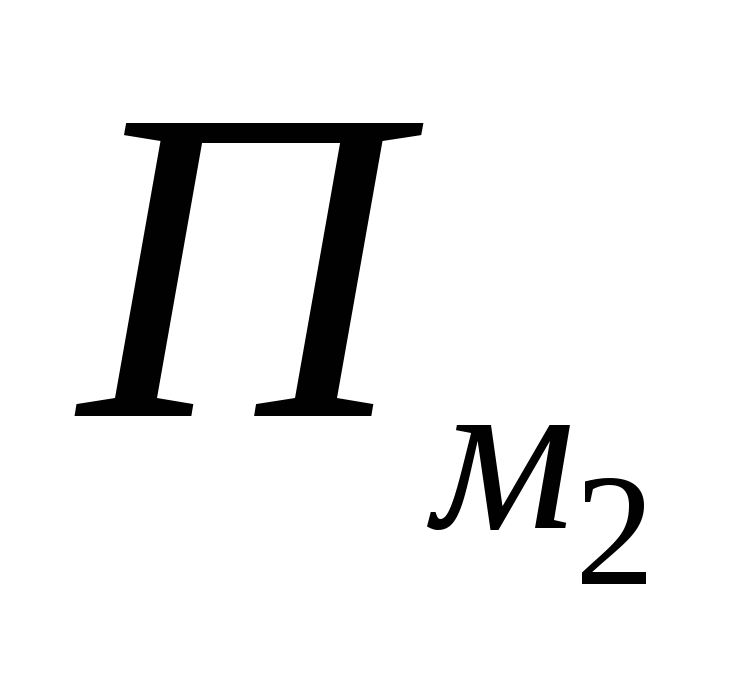- 0,5 vsak, torej prispevki takega vozlišča kP m in
so enakovredni.

Razmislite o vozliščih A in B. So mejni kot za M in za M 1 , M 2 .

Zato je prispevek vsakega od teh vozlišč kP m je enako 0,5 a in
- enoto. Zato je skupni prispevek vozlišč A in B kP m je enak 1, kar je 1 manj od njihovega prispevka k
. Ampak
, a .

Od skupnega "prispevka" vseh vozlišč P m odšteje 1 in od
odštejemo 2 in to kompenzira razliko v prispevkih vozlišč A in B.

torej
.

2. korak.

Če je poligon M z oglišči na mrežnih točkah je razrezana na dva poligona M 1 in M 2 (tudi z oglišči na vozliščih) in formula je pravilna za nekatera dva poligona MM 1 , M 2 , potem velja tudi za tretji poligon.

Na primer, naj bo res zaM 1 in M 2 , to je
... Nato (glede na prvi korak), ampak naprej prvi korak) zadnji izraz jeP m , in enakost
in obstaja Peakova formula.

3. korak.

Dokažimo Pick formulo za pravokoten trikotnik z oglišči na vozliščih mreže in kraki, ki ležijo na mrežnih linijah.

trikotnik ABC zgraditi na pravokotnik ABCD .

Za pravokotnike je Pickova formula pravilna: S ABCD = P ABCD . Glede na prvi korak P ABCD = P ABC + P ACD , P ABC = P ACD , torej P ABCD = 2p ABC . Ampak S ABCD = 2 S ABC ... Torej S ABC = P ABC .

4. korak.

Pickova formula velja za poljuben trikotnik z oglišči na točkah mreže.

Po pregledu slike je enostavno razumeti: kateri koli tak trikotnik je mogoče dobiti tako, da od pravokotnika s stranicami, ki sledijo mrežnim črtam, "odrežemo" več pravokotnikov in pravokotnih trikotnikov z nogami na mrežnih linijah. In ker Pickova formula velja za pravokotnike in pravokotne trikotnike, potem (spomni korak 2) velja tudi za prvotni trikotnik.

Dokazali smo, da če lahko poligon razrežemo na trikotnike z oglišči na vozliščih mreže, potem zanj velja Pickova formula.

3. Naloge.

Poiščite območja oblik:

1
.