По математике на тему "Формула Пика". Геометрия. Метод Пика.(Вычисление площади фигуры)

Формула Пика

1. Введение

2. Формула Пика. Доказательство I .

Доказательство II .

Доказательство Ш.

3. Задачи.

4. Формула площади многоугольника через координаты вершин.

5. Задачи.

6. Литература

Формула Пика.

1. Введение.

В истории черпаем мы мудрость,

в поэзии - остроумие,

в математике - проницательность.

Ф. Бэкон

Сюжет будет разворачиваться на обычном листке клетчатой бумаги.

Линии, идущие по сторонам клеток, образуют сетку, а вершины клеток - узлы этой сетки. Нарисуем на листе многоугольник с вершинами в узлах и найдём его площадь.

Искать её можно по - разному. Например, можно разрезать многоугольник на достаточно простые фигуры, найти их площади и сложить.

Но тут нас ждёт много хлопот. Фигура легко разбивается на прямоугольники, трапеции, и треугольники, и её площадь вычисляется без усилий.

Хотя многоугольник и выглядит достаточно просто, для вычисления его площади придется изрядно потрудиться. А если бы многоугольник выглядел более причуд­ливо? Оказывается, площади многоугольни­ков, вершины которых расположены в узлах сетки, можно вычислять гораздо проще: есть формула, связывающая их площадь с коли­чеством узлов, лежащих внутри и на границе многоугольника. Эта замечательная и простая формула называется формулой Пика.

2. Формула Пика.

Вершины многоугольника (не обязательно выпуклого) расположены в узлах целочисленной решетки. Внутри его лежит В узлов решетки, а на границе Г узлов. Докажем, что его площадь равна В + – 1 (формула Пика).

Доказательство I .

Рассмотрим многоугольник, вершины которого находятся в узлах целочисленной решётки, то есть имеют целочисленные координаты.

Многоугольник разобьём на треугольники с вершинами в узлах решётки, не содержащие узлов ни внутри, ни на сторонах.

Обозначим:

n – число сторон многоугольника,

m – количество треугольников с вершинами в узлах решётки, не содержащие узлов ни внутри, ни на сторонах,

В – число узлов внутри многоугольника,

Г – число узлов на сторонах, включая вершины.

Площади всех этих треугольников одинаковы и равны .

Следовательно, площадь многоугольника равна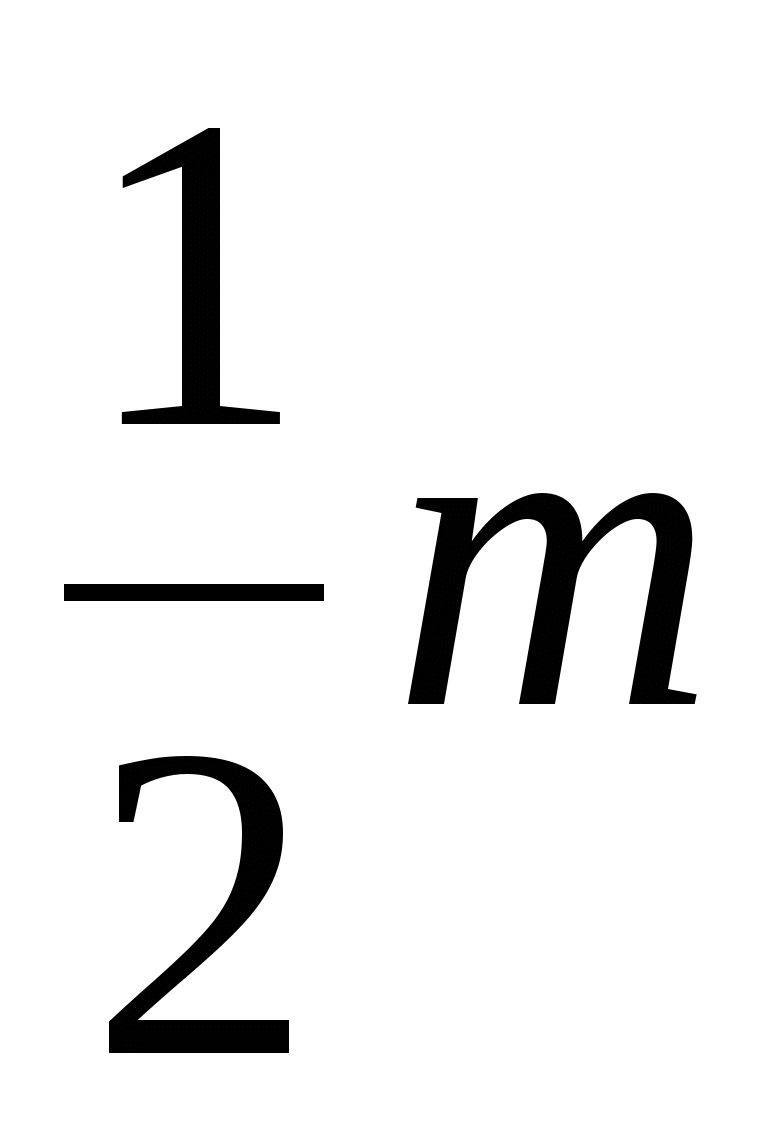
.

180 0 m .

Теперь найдём эту сумму другим способом.

Сумма углов с вершиной в любом внутреннем узле составляет 360 0 .

Тогда сумма углов с вершинами во всех внутренних узлах равна 360 0 В.

Общая сумма углов при узлах на сторонах, но не в вершинах равна 180 0 (Г – n ).

Сумма углов при вершинах многоугольника равна 180 0 (n – 2) .

Общая сумма углов всех треугольников равна 360 0 В + 180 0 (Г – n ) + 180 0 (n – 2).

Таким образом, 180 0 m = 360 0 В + 180 0 (Г – n ) + 180 0 (n – 2),

180 0 m = 360 0 В + 180 0 Г – 180 0 n + 180 0 n – 180 0 ·2,

180 0 m = 360 0 В + 180 0 Г– 360 0 ,

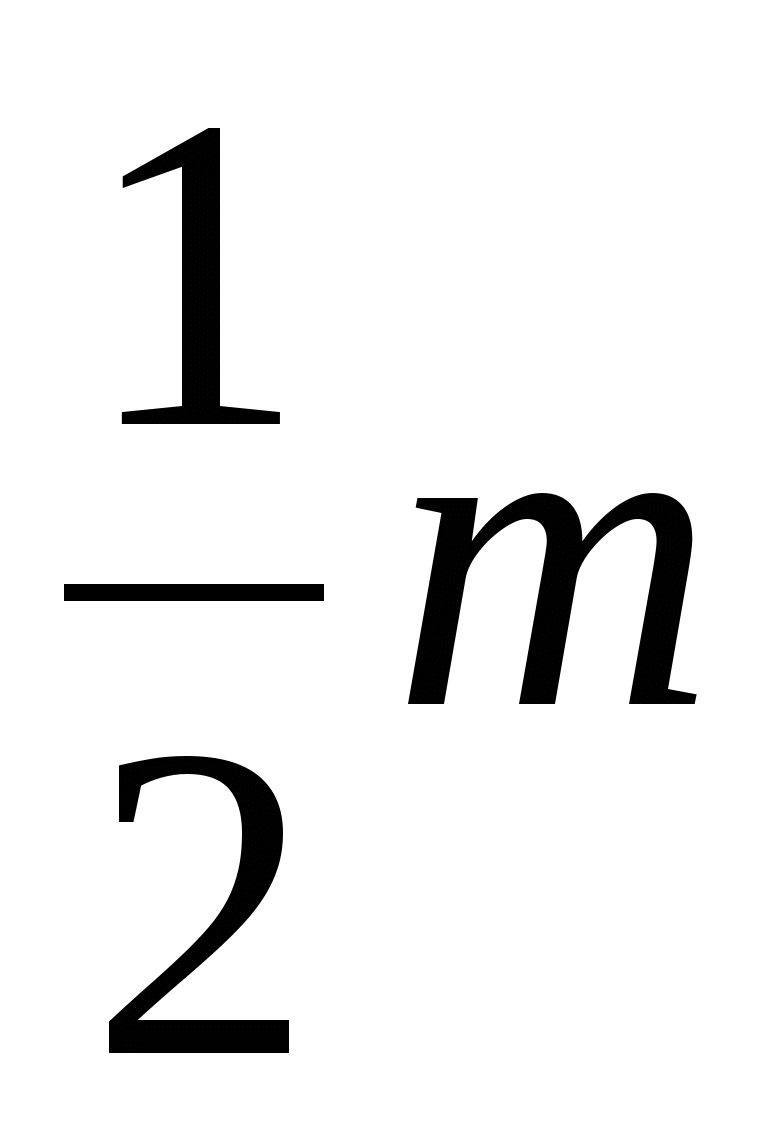= В + – 1 ,

откуда получаем выражение для площади S многоугольника:

S = В + – 1 ,

известное как формула Пика.

На рисунке: В = 24, Г = 9, следовательно, S = 24 + – 1 = 27,5.

Найдём площадь первого многоугольника по формуле Пика:

В = 28 (зеленые точки);

Г = 20 (синие точки).

Получаем, S =
= 37 кв.ед.

Доказательство II .

Каждому многоугольнику M с вершинами в узлах целочисленной решетки поставим в соответствие число f (M) =
, где суммирование ведётся по всем узлам решётки, принадлежащим M, а угол определяется следующим образом: =
для внутренней точки многоугольника, =
для граничной точки, отличной от вершины, и – угол при вершине, если данный узел – вершина. Легко видеть, что f (M) =
+
= В + – 1. Остаётся проверить, что число f (M) равно площади многоугольника M.

Пусть многоугольник M разрезан на многоугольники M 1 и M 2 с вершинами в узлах решетки. Тогда f (M) = f (M 1) + f (M 2), поскольку для каждого узла углы складываются. Поэтому если формула Пика верна для двух из многоугольников M, M 1 и M 2 , то она верна и для третьего.

Если M - прямоугольник со сторонами p и q , направленными по линиям решетки, то

f (M) = (p – 1)(q – 1) +
= pq.

В этом случае формула Пика справедлива. Разрезав прямоугольник M диагональю на треугольники M 1 и M 2 и воспользовавшись тем, что f (M) = f (M 1) + f (M 2) и f (M 1) = f (M 2), легко доказать справедливость формулы Пика для любого прямоугольного треугольника с катетами, направленными по линиям решетки. Отрезав несколько таких треугольников от прямоугольника, можно получить любой треугольник.

Для завершения доказательства формулы Пика остается заметить, что любой многоугольник можно разрезать на треугольники непересекающимися диагоналями.

Доказательство Ш.

Связь между площадью фигуры и количе­ством узлов, попавших в эту фигуру, особенно ясно видна в случае прямоугольника.

Пусть ABCD - прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки.

Обозначим через В количество узлов, лежа­щих внутри прямоугольника, а через Г - ко­личество узлов на его границе. Сместим сетку на пол клетки вправо и полклетки вниз.

Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую клетку смещенной сетки, каждый из Г – 4 гра­ничных неугловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника S равна

Итак, для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки, мы установили формулу

Докажем, что эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки.

Обозначим через S м площадь многоуголь­ника М с вершинами в узлах, а через П м – величину
, где В м – число узлов внутри М, а Г м - число узлов на границе. Тогда формулу Пика можно записать в виде
.

Доказательство формулы разобьем на не­сколько шагов.

Шаг 1.

Если многоугольник М с вершина­ми в узлах сетки разрезан на 2 многоугольни­ка М 1 и М 2 , также имеющих вершины только в узлах сетки, то
. Пусть многоугольник М разрезан на много­угольники М 1 и М 2 с вершинами в узлах отрез­ком АВ. Все узлы, кроме тех, которые попадают на отрезок АВ, дают одинаковый вклад в левую и правую части формулы. Рассмотрим узлы, лежащие на отрезке АВ.

Если такой узел лежит между А и В (на­пример, С), то для многоугольника М он внутренний, а для многоугольников М 1 и М 2 – граничный. Поэтому его вклад в П м равен 1, а в каждое из выражений
и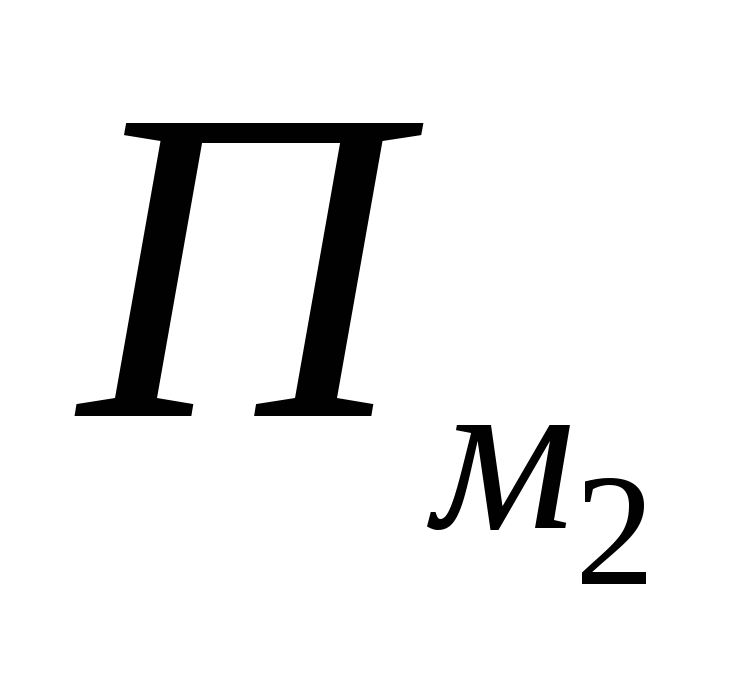
– по 0,5, то есть вклады такого узла в П м и
равны.

Рассмотрим узлы А и В. Они граничные как для М , так и для М 1 , М 2 .

Поэтому вклад каждого из этих узлов в П м равен 0,5 а в
- единице. Значит, суммарный вклад узлов А и В в П м равен 1, что на 1 меньше, чем их вклад в
. Но
, а .

Из общего «вклада» всех узлов П м вычи­тается 1, а из
вычитается 2, и это компенсирует разницу вкладов узлов А и В.

Итак,
.

Шаг 2.

Если многоугольник М с вершинами в узлах сетки разрезан на два многоугольника М 1 и М 2 (тоже с вершинами в узлах) и формула верна для каких-то двух из многоугольников М, М 1 , М 2 , то она верна и для третьего многоугольника.

Пусть, например, она верна для М 1 и М 2 , то есть
. Тогда (по первому шагу) , но (по перво­му шагу) последнее выражение равно П м , а равенство
и есть формула Пика.

Шаг 3.

Докажем формулу Пика для пря­моугольного треугольника с вершинами в узлах сетки и катетами, лежащими на линиях сетки.

Треугольник АВС достроим до прямоуголь­ника ABCD .

Для прямоугольников формула Пика верна: S ABCD = П ABCD . Согласно первому шагу П ABCD = П ABC + П ACD , П ABC = П ACD , так что П ABCD = 2П ABC . Но S ABCD = 2 S ABC . Поэтому S ABC = П ABC .

Шаг 4.

Формула Пика верна для произволь­ного треугольника с вершинами в узлах сетки.

Рассмотрев рисунок, легко понять: любой такой треугольник можно получить, «отрезав» от некоторого прямоугольника со сторонами, идущими по линиям сетки, несколько прямо­угольников и прямоугольных треугольников с катетами на линиях сетки. А так как формула Пика верна для прямоугольников и прямоугольных треугольников, то (вспомним шаг 2) она верна и для исходного треугольника.

Мы доказали, что если многоугольник мож­но разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.

3. Задачи.

Найдите площади фигур:

1
.

B = 9

Г = 4

B = 9

Г = 5

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Руководители:

• Могутова Татьяна Михайловна
• Дерюшкина Оксана Валерьевна

Девиз проекта:

“Если вы хотите научиться плавать, то смело входите в воду.
а если хотите научиться решать задачи, то решайте их”.
Д. Пойя.

Выбор темы проекта не случаен. Способы нахождения площади многоугольника нарисованного на “клеточках” очень интересная тема.

Мы знаем разные способы выполнения таких заданий: способ сложения, способ вычитания и др.

Нас очень заинтересовала эта тема, мы изучили много литературы и к нашей огромной радости нашли еще один способ, способ не известный по школьной программе, но способ замечательный! Вычисление площади, используя формулу, выведенную австрийским ученым – математиком Георгом Пиком.

Мы решили изучить формулу Пика, при помощи которой выполнять задания на нахождении площади очень легко!

Цель исследования

1. Изучение формулы Пика.

2. Расширение знаний о многообразии задач на клетчатой бумаге, о приёмах и методах решения этих задач.

Задачи:

1. Отобрать материал для исследования, выбрать главную, интересную, понятную информацию

2. Проанализировать и систематизировать полученную информацию

3. Создать электронную презентацию работы для представления собранного материала одноклассникам

4. Сделать выводы по результатам работы.

5. Подобрать наиболее интересные, наглядные примеры.

Методы исследования:

1. Моделирование

2. Построение

3. Анализ и классификация информации

4. Сравнение, обобщение

5. Изучение литературных и Интернет-ресурсов

Георг Пик – австрийский ученый – математик. Пик поступил в университет в Вене в 1875 году. Свою первую работу опубликовал в возрасте 17 лет. Круг его математических интересов был чрезвычайно широк. 67 его работ посвящены многим разделам математики, таким как: линейная алгебра, интегральное исчисление, геометрия, функциональный анализ, теория потенциала.

Широко известная Теорема появилась в сборнике работ Пика в 1899 году.

Теорема привлекла довольно большое внимание и начала вызывать восхищение своей простотой и элегантностью.

Формула Пика, формула вычисления площади многоугольника, изображенного на бумаге в клетку, полезна при решении заданий ЕГЭ и ОГЭ. Именно, поэтому, она нас очень заинтересовала.

Формула Пика - классический результат комбинаторной геометрии и геометрии чисел.

По теореме Пика площадь многоугольника равна:

Г: 2 + В – 1

Г – число узлов решетки на границе многоугольника

В – число узлов решетки внутри многоугольника.

Первым делом мы поставили задачу: изучить, что такое узлы решетки и как правильно вычислять их количество. Оказалось, это очень просто. Приведем несколько примеров.

Пусть дан произвольный треугольник. Узлы на границе изображены оранжевым цветом, узлы внутри изображены синим цветом. Найти узлы и подсчитать их количество очень легко.

В данном случае Г= 15, В = 35

Пример №2 Узлов на границе 18, т.е. Г = 18, узлов внутри 20, В = 20.

И еще один пример. Дан произвольный многоугольник. Считаем узлы на границе. Их 14. Узлом внутри многоугольника 43. Г = 14, В = 43.

С первой задачей мы справились!

Второй этап нашей работы: вычисление площадей многоугольников.

Рассмотрим несколько примеров.

Пример №1.

Г = 14, В = 43, S = + 43 – 1 = 49

Пример №2.

Г = 11, В = 5, S = + 5 – 1 = 9,5

Пример №3.

Г = 15, В = 22, S = + 22 – 1 = 28,5

Пример №4.

Г = 8, В = 16, S = + 16 – 1 = 19

Пример №5

Г = 10, В = 30, S = + 30 – 1 = 34

На рассмотрение пяти примеров мы затратили всего 1-2 минуты. Вычислять площадь по формуле Пика не только быстро, но и очень легко!

Но перед нами встал очень серьезный вопрос:

Можно ли доверять теореме Пика?

Получаются ли одинаковые результаты при вычислении площадей разными способами?

Найдем площади многоугольников по формуле Пика и обычным способом, применяя формулы геометрии и способы достроения или разбиения на части. Вот какие результаты мы получили:

Пример №1.

Вычислим площадь многоугольника по формуле Пика:

Подсчитаем количество узлов на границе и внутри. Г = 3, В = 6.

Вычислим площадь: S = 6 + - 1 = 6,5

Достроим многоугольник до прямоугольника. Площадь прямоугольника равна: 3 * 5 = 15, S? = = 3, S? = = 3 , S = = 2,5

S = 15-3-3-2,5 = 6,5

Результат одинаковый.

Пример №2.

Г = 4, В = 9, S = 9 + - 1 = 10

Достроим до прямоугольника.

Площадь прямоугольника равна: 5 * 4 = 20, S 1 = 2 * 1 = 2, S 2 = = 3,

S = = 2 , S = = 1,5, S = = 2,5

Площадь прямоугольника равна

S = 20 – 2 – 3 – 2 – 1,5 – 2,5 = 10

Мы снова получили одинаковые результаты.

Рассмотрим еще один пример.

Пример №3

Вычислим площадь по формуле Пика.

Г = 5, В = 6, S = 6 + - 1 = 7,5

Вычислим площадь, используя способ достроения.

Площадь прямоугольника равна 5·4 = 20

S 1 = 2 * 1 = 2, S 2 = = 1, S 3 = 2 * 1 = 2, S 4 = = 1, S 5 = = 1, S 6 = = 2,5

S = 20 – 2 -1– 2 – 1 – 1 – 2,5 – 3 = 7,5

Результат одинаковый.

В презентации мы рассмотрели три примера, но на самом деле мы рассмотрели очень много самых разных примеров. Результат всегда был один и тот же: Вычисление площади по формуле Пика и другими способами дает одинаковый результат.

Вывод: формуле Пика можно доверять! Она дает точный результат.

Мы довольны!

И еще один вопрос встал перед нами: какой способ вычисления наиболее рациональный, наиболее удобный для использования?

Чтобы ответить на этот вопрос, достаточно использовать всю предыдущую работу. Но рассмотрим еще три примера, которые окончательно позволят получить ответ на наш вопрос.

Пример №2

Пример №3

При помощи формулы Пика легко вычислить площадь многоугольника даже самой причудливой формы. Рассмотрим пример:

Вывод однозначный: наиболее рациональный способ вычисления площади многоугольника, изображенного на бумаге в клетку: формула Пика!

Предлагаем каждому из вас вычислить площадь многоугольника, используя формулу Пика:

Вычислите количество узлов на границе. Они изображены желтым цветом.

Вычислите количество узлов внутри, красный цвет.

Подставьте в формулу, назовите результат. Вы за одну минуту вычислили площадь.

Итак, формула Пика имеет ряд преимуществ перед другими способами вычисления площадей многоугольников на клетчатой бумаге:

Для вычисления площади многоугольника, нужно знать всего одну формулу:

S = Г:2 + В - 1.

Формула Пика очень проста для запоминания.

Формула Пика очень удобна и проста в применении.

Многоугольник, площадь которого необходимо вычислить, может быть любой, даже самой причудливой формы.

Применяя формулу Пика легко выполнять задание ЕГЭ и ОГЭ.

Приведем несколько примеров вычисления площади из вариантов ЕГЭ – 2015.

Мы решили научить пользоваться формулой Пика учащихся 9 – 11 классов нашей школы. Провели фестиваль “Формула Пика”.

Все учащиеся с большим интересом познакомились с презентацией, научились пользоваться формулой Пика.

За 30 минут практической работы учащиеся выполнили большое количество заданий. Каждый учащийся получил памятку “Формула Пика”.

Мы помогли им в подготовке к ЕГЭ и ОГЭ!

Спустя месяц работы, мы провели опрос учащихся 9–11 классом.

Задали следующие вопросы:

Вопрос №1:

Формула Пика – это рациональный способ вычисления площади многоугольника?

“Да” - 100% учащихся.

Вопрос №2:

Вы пользуетесь формулой Пика?

“Да” – 100% учащихся

Наша работа не прошла даром! Мы довольны!

Презентацию нашего проекта мы разместили в сети Интернет. Много просмотров и скачиваний нашей работы.

Мы оформили альбом “Формула Пика”. Им постоянно, особенно первое время, пользовались учащиеся нашей школы.

Результаты работы над проектом:

В процессе работы над проектом изучили справочную, научно-популярную литературу по теме исследования.

• Изучили теорему Пика, научились находить площади фигур, изображенных на бумаге в клетку просто и рационально.
• Расширили свои знания о решении задач на клетчатой бумаге, определили для себя классификацию исследуемых задач, убедились в их многообразии.
• Провели для учащихся 9–11 фестиваль “Формула Пика”, научили их находить площадь, использую эту формулу. Подобрали много интересных примеров.
• Создали электронную презентацию в помощь своим ровесникам.
• Оформили альбом “Формула Пика”, который постоянно используют учащиеся школы.

Предлагает вам выполнить два задания, чтобы вы убедились в рациональности нашей работы.

Спасибо за внимания!

Существует замечательная формула, которая позволяет считать площадь многоугольника на координатной сетке почти без ошибок. Это даже не формула, а настоящая теорема . На первый взгляд, она может показаться сложной. Но достаточно решить пару задач - и вы поймете, насколько это крутая фишка. Так что вперед!

Для начала введем новое определение:

Узел координатной стеки - это любая точка, лежащая на пересечении вертикальных и горизонтальных линий этой сетки.

Обозначение:

На первой картинке узлы вообще не обозначены. На второй обозначены 4 узла. Наконец, на третьей картинке обозначены все 16 узлов.

Какое отношение это имеет к задаче B5? Дело в том, что вершины многоугольника в таких задачах всегда лежат в узлах сетки. Как следствие, для них работает следующая теорема:

Теорема. Рассмотрим многоугольник на координатной сетке, вершины которого лежат в узлах этой сетки. Тогда площадь многоугольника равна:

где n - число узлов внутри данного многоугольника, k - число узлов, которые лежат на его границе (граничных узлов).

В качестве примера рассмотрим обычный треугольник на координатной сетке и попробуем отметить внутренние и граничные узлы.

На первой картинке дан обычный треугольник. На второй отмечены его внутренние узлы, число которых равно n = 10. На третей картинке отмечены узлы лежащие на границе, их всего k = 6.

Возможно, многим читателям непонятно, как считать числа n и k . Начните с внутренних узлов. Тут все очевидно: закрашиваем треугольник карандашом и смотрим, сколько узлов попало под закраску.

С граничными узлами чуть сложнее. Граница многоугольника - замкнутая ломаная , которая пересекает координатную сетку во многих точках. Проще всего отметить какую-нибудь «стартовую» точку, а затем обойти остальные.

Граничными узлами будут только те точки на ломаной, в которых одновременно пересекаются три линии :

1. Собственно, ломаная;
2. Горизонтальная линия координатной сетки;
3. Вертикальная линия.

Посмотрим, как все это работает в настоящих задачах.

Задача. Найдите площадь треугольника, если размер клетки равен 1 x 1 см:

Для начала отметим узлы, которые лежат внутри треугольника, а также на его границе:

Получается, что внутренний узел всего один: n = 1. Граничных узлов - целых шесть: три совпадают с вершинами треугольника , а еще три лежат на сторонах. Итого k = 6.

Теперь считаем площадь по формуле:

Вот и все! Задача решена.

Задача. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см. Ответ дайте в квадратных сантиметрах.

Снова отмечаем внутренние и граничные узлы. Внутренних узлов всего n = 2. Граничных узлов: k = 7, из которых 4 являются вершинами четырехугольника , а еще 3 лежат на сторонах.

Остается подставить числа n и k в формулу площади:

Обратите внимание на последний пример. Эту задачу реально предлагали на диагностической работе в 2012 году. Если работать по стандартной схеме, придется делать много дополнительных построений. А методом узлов все решается практически устно.

Важное замечание по площадям

Но формула - это еще не все. Давайте немного перепишем формулу, приведя слагаемые в правой части к общему знаменателю . Получим:

Числа n и k - это количество узлов, они всегда целые. Значит, весь числитель тоже целый. Мы делим его на 2, из чего следует важный факт:

Площадь всегда выражается целым числом или дробью . Причем в конце дроби всегда стоит «пять десятых»: 10,5; 17,5 и т.д.

Таким образом, площадь в задаче B5 всегда выражается целым числом или дробью вида ***,5. Если ответ получается другим, значит, где-то допущена ошибка. Помните об этом, когда будете сдавать настоящий ЕГЭ по математике!

В Викисловаре есть статья «пика» Пика В военном деле: Пика холодное колющее оружие, разновидность длинного копья. Пикинёры вид пехоты в европейских армиях XVI начала XVIII веков. Пикельхельм (п … Википедия

Теорема Пика (комбинаторная геометрия) - В=7, Г=8, В + Г/2 − 1= 10 Теорема Пика классический результат комбинаторной геометрии и геометрии чисел. Площадь многоугольника с целочисле … Википедия

Треугольник - У этого термина существуют и другие значения, см. Треугольник (значения). Треугольник (в евклидовом пространстве) это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки,… … Википедия

Трапеция - У этого термина существуют и другие значения, см. Трапеция (значения). Трапеция (от др. греч. τραπέζιον «столик»; … Википедия

Четырёхугольник - ЧЕТЫРЁХУГОЛЬНИКИ ┌─────────────┼────────────┐ невыпуклый выпуклый самопересекающийся … Википедия

Двуугольник - Правильный двуугольник на поверхности сферы Двуугольник в геометрии это … Википедия

Пятиугольник - Правильный пятиугольник (пентагон) Пятиугольник многоугольник с пятью углами. Также пятиугольником называют всякий предмет такой формы. Сумма внут … Википедия

Шестиугольник - Правильный шестиугольник Шестиугольник многоугольник с шестью углами. Также шестиугольником называют всякий предмет такой формы. Сумма внутренних углов выпуклого шестиугольника р … Википедия

Додекагон - Правильный додекагон Додекагон (греч … Википедия

Прямоугольник - Прямоугольник параллелограмм, у которого все углы прямые (равны 90 градусам). Примечание. В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые. Четвёртый угол (в силу … Википедия

Книги

• Эффект плато. Как преодолеть застой и двигаться дальше , Салливан Б.. Эффект плато - эта пугающая формула «после каждого успеха приходит застой», понимание того, что ваши усилия больше не приносят результата, - мощный закон природы, который касается каждого из… Купить за 460 руб
• Математический клуб «Кенгуру». Выпуск № 8. Математика на клетчатой бумаге , . Выпуск посвящен различным задачам и играм, связанным с листом клетчатой бумаги. В частности, в нем подробно рассматривается вычисление площади многоугольника, вершины которого расположены в…

1

Гибадуллина Г.И. (Нурлат, МАОУ СОШ №1)

1. Бунимович Е.А., Дорофеев Г.В., Суворова С.Б. и др. Математика. Арифметика. Геометрия. 5 класс: учебн. для общеобразоват. организаций с прил. на электрон. носителе -3–е изд. – М.: Просвещение, 2014. – 223, с. : ил. – (Сферы).

2. Бунимович Е.А., Кузнецова Л.В., Минаева С.С. и др. Математика. Арифметика. Геометрия. 6 класс: учебн. для общеобразоват. организаций. 5-е изд. – М.: Просвещение, 2016. – 240 с.: ил. – (Сферы).

3. Васильев Н.Б. Вокруг формулы Пика // Квант. – 1974. – №2. – С. 39–43.

4. Рассолов В.В. Задачи по планиметрии. 5–е изд., испр. и доп. – М.: 2006. – 640 с.

5. Ященко И.В. ОГЭ. Математика: типовые экзаменационные варианты: О-39 36 вариантов – М.: Изд-во «Национальное образование», 2017. – 240 с. – (ОГЭ. ФИПИ – школе).

6. Решу ОГЭ: математика. Обучающая система Дмитрия Гущина. ОГЭ-2017: задания, ответы, решения [Электронный ресурс]. – Режим доступа: https://oge.sdamgia.ru/test?id=6846966 (дата обращения 02.04.2017).

Я ученик 6 класса. Изучать геометрию начал ещё с прошлого года, ведь занимаюсь я в школе по учебнику «Математика. Арифметика. Геометрия» под редакцией Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева и другие.

Наибольшее мое внимание привлекли темы «Площади фигур», « Составление формул». Я заметил, что площади одних и тех же фигур можно находить различными способами. В быту мы часто сталкиваемся с задачами нахождения площади. Например, найти площадь пола, который придется покрасить. Любопытно ведь, чтобы купить необходимое количество обоев для ремонта, нужно знать размеры комнаты, т.е. площадь стен. Вычисление площади квадрата, прямоугольника и прямоугольного треугольника не вызывало у меня затруднений.

Заинтересовавшись этой темой, я начал искать дополнительный материал в Интернете. В результате поисков я натолкнулся на формулу Пика- это формула для вычисления площади многоугольника, нарисованного на клетчатой бумаге. Вычисление площади по этой формуле мне показалось доступным любому ученику. Именно поэтому я решил провести исследовательскую работу.

Актуальность темы . Данная тема является дополнением и углублением изучения курса геометрии.

Изучение данной темы поможет лучше подготовиться к олимпиадам и экзаменам.

Цель работы:

1. Ознакомиться с формулой Пика.

2. Овладеть приемами решений геометрических задач с использованием формулы Пика.

3. Систематизировать и обобщить теоретический и практический материалы.

Задачи исследования:

1. Проверить эффективность и целесообразность применения формулы при решении задач.

2. Научиться применять формулу Пика в задачах разной сложности.

3. Сравнить задачи, решенные с помощью формулы Пика и традиционным способом.

Основная часть

Историческая справка

Георг Александр Пик - австрийский математик , родился 10 августа года. Он был одарённым ребёнком, его обучал отец, возглавлявший частный институт. В 16 лет Георг закончил школу и поступил в Венский университет. В 20 лет получил право преподавать физику и математику. Всемирную известность ему принесла формула для определения площади решетки полигонов. Свою формулу он опубликовал в статье в 1899 году. Она стала популярной, когда польский ученый Хьюго Штейнгауз включил ее в 1969 году в издание математических снимков.

Георг Пик получил образование в Венском университете и защитил кандидатскую в 1880 году. После получения докторской степени он был назначен помощником Эрнеста Маха в Шерльско- Фердинандском университете в Праге. Там же он стал преподавателем. Он оставался в Праге до своей отставки в 1927 году, а затем вернулся в Вену.

Пик возглавлял комитет в немецком университете Праги, который назначил Эйнштейна профессором кафедры математической физики в 1911 году.

Он был избран членом Чешской академии наук и искусств, но был исключен после захвата нацистами Праги.

Когда нацисты вошли в Австрию 12 марта 1938 года, он вернулся Прагу. В марте 1939 года нацисты вторглись в Чехословакию. 13 июля 1942 года Пик был депортирован в созданный нацистами в северной Чехии лагерь Терезиенштадт, где умер две недели спустя в возрасте 82 лет.

Исследование и доказательство

Свою исследовательскую работу я начал с выяснения вопроса: площади каких фигур я смогу найти? Составить формулу для вычисления площади различных треугольников и четырехугольников я мог. А как же быть с пяти-, шести-, и вообще с многоугольниками?

В ходе исследования на различных сайтах я увидел решения задач на вычисление площади пяти-, шести-, и других многоугольников. Формула, позволяющая решать данные задачи, называлась формулой Пика. Она выглядит так: S=B+Г/2-1, где В - количество узлов, лежащих внутри многоугольника, Г - количество узлов, лежащих на границе многоугольника. Особенность данной формулы состоит в том, что её можно применять только для многоугольников, нарисованных на клетчатой бумаге.

Любой такой многоугольник легко разбить на треугольники с вершинами в узлах решётки, не содержащие узлов ни внутри, ни на сторонах. Можно показать, что площади всех этих треугольников одинаковы и равны ½, а следовательно, площадь многоугольника равна половине их числа Т.

Чтобы найти это число, обозначим через n число сторон многоугольника, через В - число узлов внутри него, через Г - число узлов на сторонах, включая вершины. Общая сумма углов всех треугольников равна 180°. Т.

Теперь найдем сумму другим способом.

Сумма углов с вершиной в любом внутреннем узле составляет 2.180°, т.е. общая сумма углов равна 360°. В; общая сумма углов при узлах на сторонах, но не в вершинах равна (Г - n)180°, а сумма углов при вершинах многоугольника будет равна (Г - 2)180°. Таким образом, Т=2.180°. В+(Г-n)180°+(n-2)180°. Выполнив раскрытие скобок и разделив на 360°, получаем формулу для площади S многоугольника, известную как формула Пика.

Практическая часть

Эту формулу решил проверить на заданиях из сборника ОГЭ-2017. Взял задачи на вычисление площади треугольника, четырехугольника и пятиугольника. Решил сравнить ответы, решая двумя способами: 1) дополнил фигуры до прямоугольника и из площади полученного прямоугольника вычел площадь прямоугольных треугольников; 2) применил формулу Пика.

S = 18-1,5-4,5 = 12 и S = 7+12/2-1= 12.

S = 24-9-3 = 12 и S = 7+12/2-1 = 12.

S = 77-7,5-12-4,5-4 =49 и S = 43+14/2-1 = 49.

Сравнив полученное, делаю вывод, что обе формулы дают один и тот же ответ. Найти площадь фигуры по формуле Пика, оказалось быстрее и легче, ведь вычислений было меньше. Легкость решения и экономия времени на вычислениях мне пригодятся в будущем при сдаче ОГЭ.

Это подтолкнуло меня на проверку возможности применения формулы Пика на более сложных фигурах.

S = 0 + 4/2 -1 = 1

S = 5+11/2-1 = 9,5

S = 4+16/2-1 = 1

Заключение

Формула Пика проста в понимании и удобна в применении. Во-первых, достаточно уметь считать, делить на 2, складывать и вычитать. Во-вторых, можно найти площадь и сложной фигуры, не затратив много времени. В-третьих, эта формула работает для любого многоугольника.

Недостаток в том, что Формула Пика применима только для фигур, которые нарисованы на клетчатой бумаге и вершины лежат на узлах клеток.

Я уверен, что при сдаче выпускных экзаменов, задачи на вычисление площади фигур не будут вызывать затруднения. Ведь я уже знаком с формулой Пика.

Библиографическая ссылка

Габбазов Н.Н. ФОРМУЛА ПИКА // Старт в науке. – 2017. – № 6-1. – С. 130-132;
URL: http://science-start.ru/ru/article/view?id=908 (дата обращения: 02.03.2019).