Bet kurios dvi lygiagretainio kraštinės yra lygiagrečios. Lygiagretainis

Lygiagretainis yra keturkampis, kurio priešingos kraštinės lygiagrečios poromis (233 pav.).

Savavališkam lygiagrečiam galioja šios savybės:

1. Lygiagretainio priešingos kraštinės yra lygios.

Įrodymas. Lygiagretainyje ABCD nubrėžiame įstrižainę AC. Trikampiai ACD ir AC B yra lygūs, nes turi bendrą kraštinę AC ir dvi poras lygių kampų greta jos:

(kaip skersiniai kampai su lygiagrečiomis tiesėmis AD ir BC). Tai reiškia, kaip ir lygių trikampių, esančių priešais vienodus kampus, kraštines, ką reikėjo įrodyti.

2. Lygiagretainio priešingi kampai yra lygūs:

3. Gretimi lygiagretainio kampai, t.y., kampai, besiribojantys su viena kraštine, sumuojami ir pan.

2 ir 3 savybių įrodymas iš karto gaunamas iš lygiagrečių tiesių kampų savybių.

4. Lygiagretainio įstrižainės viena kitą dalija susikirtimo taške. Kitaip tariant,

Įrodymas. Trikampiai AOD ir BOC yra sutampa, nes jų kraštinės AD ir BC yra lygios (savybė 1), o kampai greta jų (kaip lygiagrečių tiesių skersiniai kampai). Iš čia matyti, kad atitinkamos šių trikampių kraštinės yra lygios: AO, ką ir reikėjo įrodyti.

Kiekviena iš šių keturių savybių apibūdina lygiagretainį arba, kaip sakoma, yra jam būdinga savybė, t. y. kiekvienas keturkampis, turintis bent vieną iš šių savybių, yra lygiagretainis (taigi, turi visas kitas tris savybes).

Įrodinėjimą atliksime kiekvienam turtui atskirai.

1". Jei keturkampio priešingos kraštinės yra lygios poromis, tai yra lygiagretainis.

Įrodymas. Tegu keturkampio ABCD kraštinės AD ir BC, AB ir CD atitinkamai lygios (233 pav.). Nubrėžkime įstrižainę AC. Trikampiai ABC ir CDA bus lygūs turintiems tris poras lygios pusės.

Bet tada kampai BAC ir DCA yra lygūs ir . Kraštinių BC ir AD lygiagretumas išplaukia iš kampų CAD ir ACB lygybės.

2. Jei keturkampis turi dvi lygias priešingų kampų poras, tai jis yra lygiagretainis.

Įrodymas. Leisti . Nuo tada abi kraštinės AD ir BC yra lygiagrečios (remiantis tiesių lygiagretumu).

3. Suformulavimą ir įrodymą paliekame skaitytojui.

4. Jei keturkampio įstrižainės susikirtimo taške dalija viena kitą, tai keturkampis yra lygiagretainis.

Įrodymas. Jei AO = OS, BO = OD (233 pav.), tai trikampiai AOD ir BOC yra lygūs, tarsi turi vienodi kampai(vertikaliai!) viršūnėje O, uždarytoje tarp lygių kraštinių AO ir CO, BO ir DO porų. Iš trikampių lygybės darome išvadą, kad kraštinės AD ir BC yra lygios. Kraštinės AB ir CD taip pat yra lygios, o keturkampis pagal būdingą savybę G yra lygiagretainis.

Taigi, norint įrodyti, kad duotas keturkampis yra lygiagretainis, pakanka patikrinti bet kurios iš keturių savybių pagrįstumą. Skaitytojas kviečiamas savarankiškai įrodyti kitą būdingą lygiagretainio savybę.

5. Jei keturkampis turi porą lygiagrečių lygiagrečių kraštinių, tai jis yra lygiagretainis.

Kartais bet kuri lygiagrečių lygiagretainio kraštinių pora vadinama jo pagrindais, tada kitos dvi – šoninėmis kraštinėmis. Tiesios atkarpos, statmenos dviem lygiagretainio kraštinėms, esančios tarp jų, vadinamos lygiagretainio aukščiu. Lygiagretainė pav. 234 aukštis h nubrėžtas į kraštines AD ir BC, antrasis aukštis pavaizduotas atkarpa .

Lygiagretainės samprata

1 apibrėžimas

Lygiagretainis yra keturkampis, kurio priešingos kraštinės yra lygiagrečios viena kitai (1 pav.).

1 paveikslas.

Lygiagretainis turi dvi pagrindines savybes. Panagrinėkime juos be įrodymų.

1 nuosavybė: Lygiagretainio priešingos kraštinės ir kampai yra atitinkamai lygūs.

2 nuosavybė: Lygiagretainiu nubrėžtos įstrižainės dalinamos pusiau pagal jų susikirtimo tašką.

Lygiagretainio ženklai

Panagrinėkime tris lygiagretainio charakteristikas ir pateikime jas teoremų pavidalu.

1 teorema

Jei dvi keturkampio kraštinės yra lygios viena kitai ir lygiagrečios, tai šis keturkampis bus lygiagretainis.

Įrodymas.

Pateikiame keturkampį $ABCD$. Kuriame $AB||CD$ ir $AB=CD$ Nubrėžkime įstrižainę $AC$ (2 pav.).

2 pav.

Apsvarstykite lygiagrečias tieses $AB$ ir $CD$ bei jų sekantą $AC$. Tada

\[\angle CAB=\angle DCA\]

kaip kryžminiai kampai.

Pagal $I$ trikampių lygybės kriterijų,

nes $AC$ yra jų bendra pusė, o $AB=CD$ pagal sąlygą. Reiškia

\[\angle DAC=\angle ACB\]

Apsvarstykite tieses $AD$ ir $CB$ bei jų atkarpą $AC$; pagal paskutinę lygybę tarp gulėjimo kampų gauname $AD||CB$.) Vadinasi, pagal apibrėžimą $1$ šis keturkampis yra lygiagretainis.

Teorema įrodyta.

2 teorema

Jei priešingos keturkampio kraštinės yra lygios viena kitai, tai yra lygiagretainis.

Įrodymas.

Pateikiame keturkampį $ABCD$. Kuriame $AD=BC$ ir $AB=CD$. Nubrėžkime jame įstrižainę $AC$ (3 pav.).

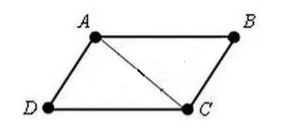
3 pav.

Kadangi $AD=BC$, $AB=CD$ ir $AC$ yra bendra kraštinė, tai pagal $III$ trikampių lygybės kriterijų,

\[\triangle DAC=\triangle ACB\]

\[\angle DAC=\angle ACB\]

Panagrinėkime eilutes $AD$ ir $CB$ bei jų sekantą $AC$; pagal paskutinę lygybę skersai gulinčių kampų gauname $AD||CB$. Todėl pagal apibrėžimą $1$ šis keturkampis yra lygiagretainis.

\[\angle DCA=\angle CAB\]

Panagrinėkime eilutes $AB$ ir $CD$ bei jų sekantą $AC$; pagal paskutinę lygybę tarp gulėjimo kampų gauname, kad $AB||CD$. Todėl pagal 1 apibrėžimą šis keturkampis yra lygiagretainis.

Teorema įrodyta.

3 teorema

Jei keturkampyje nubrėžtos įstrižainės pagal jų susikirtimo tašką yra padalintos į dvi lygias dalis, tai šis keturkampis yra lygiagretainis.

Įrodymas.

Pateikiame keturkampį $ABCD$. Nubrėžkime jame įstrižaines $AC$ ir $BD$. Tegul jie susikerta taške $O$ (4 pav.).

4 pav.

Kadangi pagal sąlygą $BO=OD,\AO=OC$, o kampai $\angle COB=\kampas DOA$ yra vertikalūs, tai pagal $I$ trikampių lygybės kriterijų,

\[\triangle BOC=\triangle AOD\]

\[\angle DBC=\angle BDA\]

Apsvarstykite eilutes $BC$ ir $AD$ bei jų sekantą $BD$; pagal paskutinę gulėjimo kampų lygybę gauname, kad $BC||AD$. Taip pat $BC=AD$. Todėl pagal teoremą $1$ šis keturkampis yra lygiagretainis.

Kaip Euklido geometrijoje taškas ir tiesė yra pagrindiniai plokštumų teorijos elementai, taip lygiagretainis yra viena iš pagrindinių išgaubtų keturkampių figūrų. Iš jo, kaip siūlai iš rutulio, išplaukia „stačiakampio“, „kvadrato“, „rombo“ ir kitų geometrinių dydžių sąvokos.

Susisiekus su

Lygiagretainio apibrėžimas

išgaubtas keturkampis, susidedantis iš atkarpų, kurių kiekviena pora yra lygiagreti, geometrijoje žinomas kaip lygiagretainis.

Kaip atrodo klasikinis lygiagretainis, pavaizduotas keturkampiu ABCD. Kraštinės vadinamos bazėmis (AB, BC, CD ir AD), statmenas, nubrėžtas iš bet kurios viršūnės į priešingą šiai viršūnei pusę, vadinamas aukščiu (BE ir BF), tiesės AC ir BD – įstrižainėmis.

Dėmesio! Kvadratas, rombas ir stačiakampis yra specialūs lygiagretainio atvejai.

Šonai ir kampai: santykių ypatumai

Pagrindinės savybės, apskritai, iš anksto nustatytas paties pavadinimo, jie įrodomi teorema. Šios savybės yra tokios:

1. Priešingos pusės yra identiškos poromis.
2. Vienas prieš kitą esantys kampai poromis yra lygūs.

Įrodymas: Panagrinėkime ∆ABC ir ∆ADC, kurie gaunami padalijus keturkampį ABCD iš tiesės AC. ∠BCA=∠CAD ir ∠BAC=∠ACD, nes AC yra bendras (atitinkamai vertikalūs kampai BC||AD ir AB||CD). Iš to išplaukia: ∆ABC = ∆ADC (antrasis trikampių lygybės ženklas).

Atkarpos AB ir BC ∆ABC poromis atitinka tieses CD ir AD ∆ADC, tai reiškia, kad jos yra identiškos: AB = CD, BC = AD. Taigi ∠B atitinka ∠D ir jie yra lygūs. Kadangi ∠A=∠BAC+∠CAD, ∠C=∠BCA+∠ACD, kurios taip pat poromis yra identiškos, tada ∠A = ∠C. Turtas įrodytas.

Figūros įstrižainių charakteristikos

Pagrindinis bruožasšių lygiagretainio tiesių: susikirtimo taškas dalija jas pusiau.

Įrodymas: Tegul t.y. yra figūros ABCD įstrižainių AC ir BD susikirtimo taškas. Jie sudaro du proporcingus trikampius – ∆ABE ir ∆CDE.

AB = CD, nes jie yra priešingi. Pagal linijas ir sekantą ∠ABE = ∠CDE ir ∠BAE = ∠DCE.

Pagal antrąjį lygybės kriterijų ∆ABE = ∆CDE. Tai reiškia, kad elementai ∆ABE ir ∆CDE: AE = CE, BE = DE ir kartu jie yra proporcingos AC ir BD dalys. Turtas įrodytas.

Gretimų kampų ypatybės

Gretimose pusėse kampų suma lygi 180°, nes jie yra toje pačioje pusėje lygiagrečių linijų ir skersinės. Keturkampiui ABCD:

∠A+∠B=∠C+∠D=∠A+∠D=∠B+∠C=180º

Bisektoriaus savybės:

1. , nuleistas į vieną pusę, yra statmenos;
2. priešingos viršūnės turi lygiagrečius bisektorius;
3. trikampis, gautas nubrėžus pusiaukampį, bus lygiašonis.

Lygiagretainio charakteristikų nustatymas taikant teoremą

Šios figūros charakteristikos išplaukia iš pagrindinės jo teoremos, kuri teigia: keturkampis laikomas lygiagretainiu tuo atveju, jei jo įstrižainės susikerta, ir šis taškas padalija jas į lygias atkarpas.

Įrodymas: tegul keturkampio ABCD tiesės AC ir BD susikerta t.y. Kadangi ∠AED = ∠BEC ir AE+CE=AC BE+DE=BD, tai ∆AED = ∆BEC (pagal pirmąjį trikampių lygybės kriterijų). Tai yra, ∠EAD = ∠ECB. Jie taip pat yra vidiniai skersinio AC linijos kampai AD ir BC. Taigi, pagal paralelizmo apibrėžimą - AD || B.C. Taip pat gaunama panaši eilučių BC ir CD savybė. Teorema įrodyta.

Figūros ploto apskaičiavimas

Šios figūros plotas randama keliais būdais vienas iš paprasčiausių: padauginti aukštį ir pagrindą, prie kurio jis traukiamas.

Įrodymas: iš viršūnių B ir C nubrėžkite statmenis BE ir CF. ∆ABE ir ∆DCF yra lygūs, nes AB = CD ir BE = CF. ABCD dydis yra lygus stačiakampiui EBCF, nes juos sudaro proporcingos figūros: S ABE ir S EBCD, taip pat S DCF ir S EBCD. Iš to išplaukia, kad ši sritis geometrinė figūra yra taip pat kaip stačiakampis:

S ABCD = S EBCF = BE × BC = BE × AD.

Norėdami nustatyti bendrą lygiagretainio ploto formulę, pažymime aukštį kaip hb, o šonas - b. Atitinkamai:

Kiti būdai rasti plotą

Ploto skaičiavimai per lygiagretainio kraštines ir kampą, kurį jie sudaro, yra antrasis žinomas metodas.

,

Spr-ma - plotas;

a ir b yra jos kraštinės

α yra kampas tarp atkarpų a ir b.

Šis metodas praktiškai pagrįstas pirmuoju, bet tuo atveju, jei jis nežinomas. visada nukerpa statųjį trikampį, kurio parametrai randami trigonometrinės tapatybės, tai yra . Pakeitę santykį, gauname . Pirmojo metodo lygtyje aukštį pakeičiame šiuo produktu ir gauname šios formulės pagrįstumo įrodymą.

Per lygiagretainio įstrižaines ir kampą, kurią jie sukuria susikirsdami, taip pat galite rasti sritį.

Įrodymas: AC ir BD susikerta ir sudaro keturis trikampius: ABE, BEC, CDE ir AED. Jų suma lygi šio keturkampio plotui.

Kiekvieno iš šių ∆ plotą galima rasti pagal išraišką , kur a=BE, b=AE, ∠γ =∠AEB. Nuo , skaičiuojant naudojama viena sinuso reikšmė. Tai yra . Kadangi AE+CE=AC=d 1 ir BE+DE=BD=d 2, ploto formulė sumažinama iki:

.

Taikymas vektorinėje algebroje

Šio keturkampio sudedamųjų dalių savybės buvo pritaikytos vektorių algebroje, būtent dviejų vektorių pridėjimas. Lygiagretainio taisyklė teigia, kad jei pateikti vektoriaiIrNeyra kolinearūs, tada jų suma bus lygi šios figūros, kurios pagrindai atitinka šiuos vektorius, įstrižai.

Įrodymas: nuo savavališkai pasirinktos pradžios – t.y. - sudaryti vektorius ir . Toliau sukonstruojame lygiagretainį OASV, kur atkarpos OA ir OB yra kraštinės. Taigi, OS yra ant vektoriaus arba sumos.

Lygiagretainio parametrų skaičiavimo formulės

Tapatybės suteikiamos tokiomis sąlygomis:

1. a ir b, α - kraštinės ir kampas tarp jų;
2. d 1 ir d 2, γ - įstrižainės ir jų susikirtimo taške;
3. h a ir h b - aukščiai nuleisti į a ir b puses;

Parametras	Formulė
Šonų radimas
išilgai įstrižainių ir kampo tarp jų kosinuso
išilgai įstrižainių ir šonų
per aukštį ir priešingą viršūnę
Įstrižainių ilgio radimas
šonuose ir viršūnės tarp jų dydis

Sign-ki pa-ral-le-lo-gram-ma

1. Lygiagretainio apibrėžimas ir pagrindinės savybės

Pradėkime primindami para-ral-le-lo-gram apibrėžimą.

Apibrėžimas. Lygiagretainis- what-you-rekh-gon-nick, kuris turi kas dvi pro-ti-false puses, kurios yra lygiagrečios (žr. 1 pav.).

Ryžiai. 1. Pa-ral-le-lo-gram

Prisiminkime pagrindinės pa-ral-le-lo-gram-ma savybės:

Kad galėtumėte naudotis visomis šiomis savybėmis, turite būti tikri, kad fi-gu-ra, apie ką nors -Roy mes kalbame apie, - pa-ral-le-lo-gram. Norėdami tai padaryti, turite žinoti tokius faktus kaip pa-ral-le-lo-gram-ma požymius. Dabar žiūrime į pirmuosius du iš jų.

2. Pirmasis lygiagretainio ženklas

Teorema. Pirmasis pa-ral-le-lo-gram-ma ženklas. Jei keturių anglių dvi priešingos pusės yra lygios ir lygiagrečios, tada ši keturių anglių slapyvardis - lygiagretainis. .

Ryžiai. 2. Pirmasis pa-ral-le-lo-gram-ma požymis

Įrodymas. Įdėkime dia-go-nalą į keturių-reh-coal-ni-ka (žr. 2 pav.), ji padalija ją į dvi tri-coal-ni-ka. Parašykime, ką žinome apie šiuos trikampius:

pagal pirmąjį trikampių lygybės ženklą.

Iš nurodytų trikampių lygybės matyti, kad tiesių linijų lygiagretumo ženklu kertant ch-nii jų s-ku-shchi. Turime tai:

Do-ka-za-but.

3. Antrasis lygiagretainio ženklas

Teorema. Antrasis ženklas yra pa-ral-le-lo-gram-ma. Jei keturių kampų kas dvi pro-ti-false pusės yra lygios, tada šis keturių kampų yra lygiagretainis. .

Ryžiai. 3. Antrasis pa-ral-le-lo-gram-ma ženklas

Įrodymas. Į keturių kampų kampą įdedame dia-go-nalą (žr. 3 pav.), ji padalija į du trikampius. Remdamiesi teorijos forma, užrašykite, ką žinome apie šiuos trikampius:

pagal trečiąjį trikampių lygybės ženklą.

Iš trikampių lygybės išplaukia, kad pagal lygiagrečių linijų ženklą, kai jas susikerta, s-ku-shchey. Pavalgykime:

par-ral-le-lo-gram pagal apibrėžimą. Q.E.D.

Do-ka-za-but.

4. Pirmojo lygiagretainio požymio panaudojimo pavyzdys

Pažvelkime į pa-ral-le-lo-gram ženklų naudojimo pavyzdį.

Pavyzdys 1. Iškilime nėra anglių Raskite: a) anglių kampus; b) šimtaro šulinys.

Sprendimas. Iliustracija Fig. 4.

pa-ral-le-lo-gram pagal pirmąjį pa-ral-le-lo-gram-ma ženklą.

A. pagal par-ral-le-lo-gramo savybę apie pro-ti-klaidingus kampus, pagal par-ral-le-lo-gramo savybę apie kampų sumą, kai gulima į vieną pusę.

B. pagal melagingų pusių lygybės prigimtį.

re-tiy ženklas pa-ral-le-lo-gram-ma

5. Apžvalga: lygiagretės apibrėžimas ir savybės

Prisiminkime tai lygiagretainis- tai keturių kvadratų kampas, turintis pro-ti-false puses poromis. Tai yra, jei - par-ral-le-lo-gram, tada (žr. 1 pav.).

Lygiagreti-le-lo-grama turi daugybę savybių: priešingi kampai yra lygūs (), priešingi kampai - mes lygūs ( ). Be to, dia-go-na-li pa-ral-le-lo-gram-ma taške re-se-che-niya padalijama pagal kampų sumą, at-le- spaudžiant bet kurią šoninis pa-ral-le-lo-gram-ma, lygus ir kt.

Tačiau norint pasinaudoti visomis šiomis savybėmis, būtina būti visiškai tikram, kad ri-va-e-my th-you-rekh-coal-nick - pa-ral-le-lo-gram. Šiuo tikslu yra par-ral-le-lo-gram ženklai: tai yra tie faktai, iš kurių galima padaryti vienareikšmę išvadą, kad what-you-rekh-coal-nickas yra par-ral- le-lo-gram-mama. Ankstesnėje pamokoje jau žiūrėjome į du ženklus. Dabar žiūrime trečią kartą.

6. Trečiasis lygiagretainio ženklas ir jo įrodymas

Jei keturių anglių taške yra dia-go-on re-se-che-niya taške jie daro-by-lams, tada duota keturių jums Roh-coal-nicck yra pa-ral-le -lo-gram-mama.

Duota:

What-you-re-anglies nick; ; .

Įrodykite:

Lygiagretainis.

Įrodymas:

Norint įrodyti šį faktą, būtina parodyti šalių paraleliškumą par-le-lo-gramai. O tiesių linijų lygiagretumas dažniausiai pasiekiamas per vidinių kryžminių kampų lygybę šiais stačiais kampais. Taigi, čia yra kitas būdas gauti trečiąjį par-ral -le-lo-gram-ma ženklą: per trikampių lygybę .

Pažiūrėkime, kaip šie trikampiai yra lygūs. Iš tiesų, iš sąlygos išplaukia: . Be to, kadangi kampai yra vertikalūs, jie yra lygūs. Tai yra:

(pirmasis lygybės ženklastri-coal-ni-cov- išilgai dviejų pusių ir kampe tarp jų).

Iš trikampių lygybės: (kadangi vidiniai skersiniai kampai ties šiomis tiesėmis ir skyrikliais yra lygūs). Be to, iš trikampių lygybės išplaukia, kad . Tai reiškia, kad mes suprantame, kad keturiuose angliuose du šimtai yra lygūs ir lygiagrečiai. Pagal pirmąjį ženklą pa-ral-le-lo-gram-ma: - pa-ral-le-lo-gram.

Do-ka-za-but.

7. Trečiojo lygiagretainio ženklo uždavinio pavyzdys ir apibendrinimas

Pažvelkime į trečiojo pa-ral-le-lo-gram ženklo naudojimo pavyzdį.

1 pavyzdys

Duota:

- lygiagretainis; . - se-re-di-na, - se-re-di-na, - se-re-di-na, - se-re-di-na (žr. 2 pav.).

Įrodykite:- pa-ral-le-lo-gram.

Įrodymas:

Tai reiškia, kad keturių anglių-no-dia-go-on-ar tuo re-se-che-niya taško jie daro-by-lam. Pagal trečiąjį pa-ral-le-lo-gram ženklą iš to išplaukia, kad - pa-ral-le-lo-gram.

Do-ka-za-but.

Jei analizuosite trečiąjį pa-ral-le-lo-gram ženklą, galite pastebėti, kad šis ženklas yra su-vet- turi par-ral-le-lo-gram savybę. Tai yra faktas, kad dia-go-na-li de-la-xia nėra tik par-le-lo-gram savybė, o jos skiriamoji, kha-rak-te-ri-sti-che- savybė, pagal kurią ją galima atskirti nuo aibės what-you-rekh-coal-ni-cov.

ŠALTINIS

http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/priznaki-parallelogramma

http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/tretiy-priznak-parallelogramma

http://www.uchportfolio.ru/users_content/675f9820626f5bc0afb47b57890b466e/images/46TThxQ8j4Y.jpg

http://cs10002.vk.me/u31195134/116260458/x_56d40dd3.jpg

http://www.tepka.ru/geometriya/16.1.gif

Lygiagretainis yra keturkampis, kurio priešingos kraštinės yra lygiagrečios poromis. Toliau pateiktame paveikslėlyje parodytas lygiagretainis ABCD. Jos kraštinė AB lygiagreti kraštinei CD ir kraštinė BC lygiagreti kraštinei AD.

Kaip jau spėjote, lygiagretainis yra išgaubtas keturkampis. Panagrinėkime pagrindines lygiagretainio savybes.

Lygiagretainio savybės

1. Lygiagrečiame priešingi kampai ir priešingos kraštinės yra lygūs. Įrodykime šią savybę – apsvarstykite lygiagretainį, pateiktą sekančiame paveikslėlyje.

Įstrižainė BD padalija ją į dvi dalis lygus trikampis: ABD ir CBD. Jie yra lygūs išilgai kraštinės BD ir dviejų šalia jos esančių kampų, nes kampai yra kryžminiai lygiagrečių tiesių BC ir AD bei AB ir CD skersinėje BD. Todėl AB = CD ir
BC = po Kr. O iš 1, 2, 3 ir 4 kampų lygybės išplaukia, kad kampas A = kampas1 + kampas3 = kampas2 + kampas4 = kampas C.

2. Lygiagretainio įstrižainės dalijamos per pusę susikirtimo taško. Tegul taškas O yra lygiagretainio ABCD įstrižainių AC ir BD susikirtimo taškas.

Tada trikampis AOB ir trikampis COD yra lygūs vienas kitam, išilgai šono ir dviejų gretimų kampų. (AB = CD, nes tai yra priešingos lygiagretainio kraštinės. O kampas1 = kampas2 ir kampas3 = kampas4 yra kaip kryžminiai kampai, kai tiesės AB ir CD susikerta atitinkamai su sekantais AC ir BD.) Iš to išplaukia, kad AO = OC ir OB = OD, kurį ir reikėjo įrodyti.

Visos pagrindinės savybės parodytos trijuose paveikslėliuose.