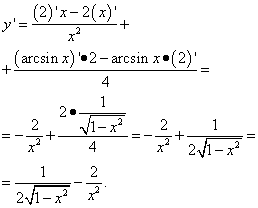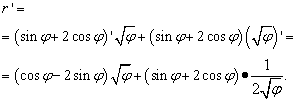Derivată a cosinusului: (cos x)′. Derivate ale funcțiilor trigonometrice: tangentă, sinus, cosinus și altele

Găsiți derivata.

Opțiunea 1.

Opțiunea 2.

la = 2X + 5.

la = 2X – 5.

la= 4cos X.

la= 3sin X.

la= tg X+ctg X.

la= tg X-ctg X.

la= păcatul 3 X.

la= cos 4 X.

Opțiuni de răspuns.

– 4sin X

– 3cos X

1/cos 2 X+ 1/sin 2 X

1/cos 2 X–1/păcat 2 X

1/păcat 2 X–1/cos 2 X

– 4sin4 X

– 3cos3 X

f(X) = păcat X+cos X

f(X) = sin 2 X – X

f(X) = 2X+cos(4 X – )

Opțiunea 1

Opțiunea 2

y = 2X 3

y = 3X 2

y = 1/4 X 4 + 2X 2 – 7

y = 1/2 X 4 + 4X + 5

y = X 3 + 4X 2 – 3X.
Rezolvați ecuația y " = 0

y = 2X 3 – 9X 2 + 12X + 7.
Rezolvați ecuația y " = 0.

y= păcatul 2 X– cos 3 X.

y= cos 2 X– păcatul 3 X.

y= tg X–ctg( X + /4).

y=ctg X+ tg( X – /4).

y= păcatul 2 X.

y= cos 2 X.

Opțiuni de răspuns.

Când obținem prima formulă a tabelului, vom porni de la definiția funcției derivate într-un punct. Să luăm unde X- orice numar real, acesta este, X– orice număr din domeniul de definire al funcției. Să notăm limita raportului dintre incrementul funcției și incrementul argumentului la:

De remarcat că sub semnul limită se obține expresia, care nu este incertitudinea zero împărțită la zero, întrucât numărătorul nu conține o valoare infinitezimală, ci exact zero. Cu alte cuvinte, incrementul unei funcții constante este întotdeauna zero.

Prin urmare, derivata unei functii constanteeste egal cu zero în întregul domeniu de definiție.

Derivată a unei funcții de putere.

Formula pentru derivata unei funcții putere are forma , unde exponentul p– orice număr real.

Să demonstrăm mai întâi formula exponentului natural, adică pentru p = 1, 2, 3, …

Vom folosi definiția derivatei. Să notăm limita raportului dintre incrementul unei funcții de putere și incrementul argumentului:

Pentru a simplifica expresia în numărător, ne întoarcem la formula binomială Newton:

Prin urmare,

Aceasta dovedește formula pentru derivata unei funcții de putere pentru un exponent natural.

Derivată a unei funcții exponențiale.

Prezentăm derivarea formulei derivate pe baza definiției:

Am ajuns la incertitudine. Pentru a o extinde, introducem o nouă variabilă, iar la . Apoi . În ultima tranziție, am folosit formula pentru trecerea la o nouă bază logaritmică.

Să înlocuim în limita inițială:

Dacă ne amintim a doua limită remarcabilă, ajungem la formula pentru derivata funcției exponențiale:

Derivată a unei funcții logaritmice.

Să demonstrăm formula pentru derivata unei funcții logaritmice pentru toate X din domeniul definiției și toate valorile valide ale bazei A logaritm Prin definiția derivatei avem:

După cum ați observat, în timpul demonstrației transformările au fost efectuate folosind proprietățile logaritmului. Egalitatea este adevărat datorită celei de-a doua limite remarcabile.

Derivate ale funcţiilor trigonometrice.

Pentru a deriva formule pentru derivate ale funcțiilor trigonometrice, va trebui să reamintim câteva formule de trigonometrie, precum și prima limită remarcabilă.

Prin definiția derivatei pentru funcția sinus avem .

Să folosim formula diferenței sinusurilor:

Rămâne să ne întoarcem la prima limită remarcabilă:

Astfel, derivata funcției sin x Există cos x.

Formula pentru derivata cosinusului este dovedită exact în același mod.

Prin urmare, derivata funcției cos x Există –sin x.

Vom obține formule pentru tabelul de derivate pentru tangentă și cotangentă folosind reguli dovedite de diferențiere (derivată a unei fracții).

Derivate ale funcțiilor hiperbolice.

Regulile de diferențiere și formula pentru derivata funcției exponențiale din tabelul derivatelor ne permit să derivăm formule pentru derivatele sinusului hiperbolic, cosinusului, tangentei și cotangentei.

Derivată a funcției inverse.

Pentru a evita confuzia în timpul prezentării, să notăm în indice argumentul funcției prin care se realizează diferențierea, adică este derivata funcției f(x) De X.

Acum să formulăm regula pentru aflarea derivatei unei functii inverse.

Lasă funcțiile y = f(x)Și x = g(y) reciproc invers, definite pe intervale și respectiv. Dacă într-un punct există o derivată finită nenulă a funcției f(x), atunci în punct există o derivată finită a funcției inverse g(y), și . Într-o altă postare .

Această regulă poate fi reformulată pentru oricare X din intervalul , atunci obținem .

Să verificăm validitatea acestor formule.

Să găsim funcția inversă pentru logaritmul natural (Aici y este o funcție și X- argument). După ce am rezolvat această ecuație pt X, primim (aici X este o funcție și y– argumentul ei). Acesta este, și funcții reciproc inverse.

Din tabelul derivatelor vedem că Și .

Să ne asigurăm că formulele pentru găsirea derivatelor funcției inverse ne conduc la aceleași rezultate:

Se prezintă demonstrația și derivarea formulei pentru derivata cosinusului - cos(x). Exemple de calculare a derivatelor de cos 2x, cos 3x, cos nx, cosinus pătrat, cub și la puterea n. Formula pentru derivata cosinusului de ordinul al n-lea.

Derivata față de variabila x din cosinusul lui x este egală cu minus sinusul lui x:
(cos x)′ = - sin x.

Dovada

Pentru a deriva formula pentru derivata cosinusului, folosim definiția derivatei:
.

Să transformăm această expresie pentru a o reduce la legile și regulile matematice cunoscute. Pentru a face acest lucru, trebuie să cunoaștem patru proprietăți.
1) Formule trigonometrice. Vom avea nevoie de următoarea formulă:
(1) ;
2) Proprietatea de continuitate a funcției sinus:
(2) ;
3) Semnificația primei limite remarcabile:
(3) ;
4) Proprietatea limitei produsului a două funcții:
Dacă și , atunci
(4) .

Să aplicăm aceste legi până la limita noastră. Mai întâi transformăm expresia algebrică
.
Pentru a face acest lucru, aplicăm formula
(1) ;
În cazul nostru
; . Apoi
;
;
;
.

Să facem o înlocuire. La , . Folosim proprietatea continuității (2):
.

Să facem aceeași înlocuire și să aplicăm prima limită remarcabilă (3):
.

Deoarece limitele calculate mai sus există, aplicăm proprietatea (4):

.

Astfel, am obținut formula pentru derivata cosinusului.

Exemple

Sa luam in considerare exemple simple găsirea derivatelor de funcții care conțin cosinus. Să găsim derivatele lui următoarele funcții:
y = cos 2x; y = cos 3x; y = cos nx; y = cos 2 x; y = cos 3 xși y = cos n x.

Exemplul 1

Găsiți derivate ale cos 2x, cos 3xȘi cosnx.

Soluţie

Funcțiile originale au o formă similară. Prin urmare vom găsi derivata funcției y = cosnx. Apoi, ca derivat al cosnx, înlocuiți n = 2 și n = 3 . Și, astfel, obținem formule pentru derivatele lui ca 2xȘi cos 3x .

Deci, găsim derivata funcției
y = cosnx .
Să ne imaginăm această funcție a variabilei x ca o funcție complexă constând din două funcții:
1)
2)
Atunci funcția originală este o funcție complexă (compozită) compusă din funcții și:
.

Să găsim derivata funcției față de variabila x:
.
Să găsim derivata funcției în raport cu variabila:
.
Aplicam.
.
Să înlocuim:
(P1) .

Acum, în formula (A1) înlocuim și:
;
.

Răspuns

;
;
.

Exemplul 2

Aflați derivatele cosinus pătrat, cosinus cub și cosinus la puterea n:
y = cos 2 x; y = cos 3 x; y = cos n x.

Soluţie

În acest exemplu, funcțiile au, de asemenea, un aspect similar. Prin urmare, vom găsi derivata celor mai multe functia generala- cosinus la puterea n:
y = cos n x.
Apoi înlocuim n = 2 și n = 3. Și, astfel, obținem formule pentru derivatele cosinus pătrat și cosinus cub.

Deci trebuie să găsim derivata funcției
.
Să-l rescriem într-o formă mai înțeleasă:
.
Să ne imaginăm această funcție ca o funcție complexă constând din două funcții:
1) Funcții în funcție de o variabilă: ;
2) Funcţii în funcţie de o variabilă: .
Atunci funcția originală este o funcție complexă compusă din două funcții și:
.

Aflați derivata funcției față de variabila x:
.
Aflați derivata funcției în raport cu variabila:
.
Aplicam regula de diferentiere a functiilor complexe.
.
Să înlocuim:
(P2) .

Acum să înlocuim și:
;
.

Răspuns

;
;
.

Derivate de ordin superior

Rețineți că derivata lui cos x ordinul întâi poate fi exprimat prin cosinus după cum urmează:
.

Să găsim derivata de ordinul doi folosind formula pentru derivata unei funcții complexe:

.
Aici .

Rețineți că diferențierea cos x face ca argumentul său să crească cu . Atunci derivata de ordinul n-a are forma:
(5) .

Această formulă poate fi dovedită mai strict folosind metoda inducției matematice. Dovada pentru derivata a n-a a sinusului este prezentată pe pagina „Derivată a sinusului”. Pentru derivata a n-a a cosinusului, demonstrația este exact aceeași. Trebuie doar să înlocuiți sin cu cos în toate formulele.

Sunt prezentate derivatele funcțiilor trigonometrice inverse și derivarea formulelor acestora. Sunt date și expresii pentru derivate de ordin superior. Link-uri către pagini cu o descriere mai detaliată a derivării formulelor.

În primul rând, derivăm formula pentru derivata arcsinusului. Lăsa
y = arcsin x.
Deoarece arcsinus este funcția inversă a sinusului, atunci
.
Aici y este o funcție a lui x. Diferențierea față de variabila x:
.
Aplicam:
.
Așa că am găsit:
.

Pentru că atunci . Apoi
.
Și formula anterioară ia forma:
. De aici
.

Exact în acest fel, puteți obține formula pentru derivata arccosinusului. Cu toate acestea, este mai ușor să utilizați o formulă care să relaționeze funcțiile trigonometrice inverse:
.
Apoi
.

O descriere mai detaliată este prezentată în pagina „Derivarea derivaților arcsinusului și arccosinului”. Acolo este dat derivarea derivatelor în două moduri- discutat mai sus și conform formulei pentru derivata funcției inverse.

Derivarea derivaților arctangentei și arccotangentei

În același mod vom găsi derivatele arctangent și arccotangent.

Lăsa
y = arctan x.
Arctangenta este funcția inversă a tangentei:
.
Diferențierea față de variabila x:
.
Aplicam formula pentru derivata unei functii complexe:
.
Așa că am găsit:
.

Derivată a cotangentei arcului:
.

Derivați de arcsin

Lăsa
.
Am găsit deja derivata de ordinul întâi a arcsinusului:
.
Prin diferențiere, găsim derivata de ordinul doi:
;
.
Poate fi scris și sub următoarea formă:
.
De aici obținem o ecuație diferențială care este satisfăcută de derivatele arcsinusului de ordinul întâi și al doilea:
.

Prin diferențierea acestei ecuații, putem găsi derivate de ordin superior.

Derivată de arcsinus de ordinul al n-lea

Derivata arcsinusului de ordinul n are următoarea vedere:
,
unde este un polinom de grad . Acesta este determinat de formulele:
;
.
Aici .

Polinomul satisface ecuația diferențială:
.

Derivată a arccosinului de ordinul al n-lea

Derivatele pentru arc cosinus sunt obținute din derivate pentru arc sinus folosind formula trigonometrică:
.
Prin urmare, derivatele acestor funcții diferă doar prin semn:
.

Derivate ale arctangentei

Lăsa . Am găsit derivata cotangentei arcului de ordinul întâi:
.

Să descompunem fracția în cea mai simplă formă:

.
Iată unitatea imaginară, .

Diferențiem o dată și aducem fracția la un numitor comun:

.

Înlocuind , obținem:
.

Derivată arctangentei de ordinul al n-lea

Astfel, derivata arctangentei de ordinul al n-lea poate fi reprezentată în mai multe moduri:
;
.

Derivate ale arcului cotangent

Să fie acum. Să aplicăm formula care conectează funcțiile trigonometrice inverse:
.
Atunci derivata de ordinul al n-lea a arc-tangentei diferă doar prin semn de derivata arc-tangentei:
.

Înlocuind , găsim:
.

Referinte:
N.M. Gunter, R.O. Kuzmin, Culegere de probleme de matematică superioară, „Lan”, 2003.

A găsi derivata unei functii trigonometrice nevoie de utilizare tabelul derivatelor, şi anume derivatele 6-13.

Cand gasesti derivate ale funcţiilor trigonometrice simple Pentru a evita greșelile comune, ar trebui să acordați atenție următoarelor puncte:

• într-o expresie de funcție, unul dintre termeni este adesea sinus, cosinus sau altă funcție trigonometrică nu din argumentul funcției, ci din număr (constante), deci derivata acestui termen este egală cu zero;
• aproape întotdeauna trebuie să simplificați expresia obținută ca urmare a diferențierii, iar pentru aceasta trebuie să folosiți cu încredere cunoștințele operațiilor cu fracții;
• pentru a simplifica expresia pe care aproape întotdeauna trebuie să o știi identități trigonometrice, de exemplu, formula unghiului dublu și formula unității ca sumă a pătratelor sinusului și cosinusului.

Exemplul 1. Aflați derivata unei funcții

Soluţie. Să zicem cu derivat de cosinus totul este clar, vor spune mulți care încep să studieze derivatele. Ce ziceti derivat de sinus doisprezece împărțit la pi? Răspuns: consideră-l egal cu zero! Aici sinusul (o funcție până la urmă!) este o capcană, deoarece argumentul nu este variabila X sau orice altă variabilă, ci doar un număr. Adică, sinusul acestui număr este, de asemenea, un număr. Și derivata unui număr (constante), așa cum știm din tabelul derivatelor, este egală cu zero. Deci, lăsăm doar sinusul minus al lui X și găsim derivata acestuia, fără a uita de semnul:

.

Exemplul 2. Aflați derivata unei funcții

.

Soluţie. Al doilea termen este același caz ca primul termen din exemplul anterior. Adică este un număr, iar derivata numărului este zero. Găsim derivata celui de-al doilea termen ca derivată a coeficientului:

Exemplul 3. Aflați derivata unei funcții

Soluţie. Aceasta este o altă problemă: aici în primul termen nu există arcsinus sau altă funcție trigonometică, dar există x, ceea ce înseamnă că este o funcție a lui x. Prin urmare, îl diferențiem ca termen în suma funcțiilor:

Aici au fost necesare abilități în operațiuni cu fracții, și anume, în eliminarea structurii cu trei etaje a unei fracții.

Exemplul 4. Aflați derivata unei funcții

.

Soluţie. Aici litera „phi” joacă același rol ca „x” în cazurile anterioare (și în majoritatea celorlalte, dar nu toate) - variabila independentă. Prin urmare, atunci când căutăm derivata unui produs de funcții, nu ne vom grăbi să declarăm derivata rădăcinii lui „phi” egală cu zero. Asa de:

Dar soluția nu se termină aici. Deoarece termeni similari sunt adunați în două paranteze, încă ni se cere să transformăm (simplificam) expresia. Prin urmare, înmulțim parantezele cu factorii din spatele lor, apoi aducem termenii la un numitor comun și efectuăm alte transformări elementare:

Exemplul 5. Aflați derivata unei funcții

Soluţie. În acest exemplu, va trebui să știm faptul că există o astfel de funcție trigonometrică - secanta - și formulele sale prin cosinus. Sa facem diferenta:

Exemplul 6. Aflați derivata unei funcții

.

Soluţie. În acest exemplu, ni se va cere să ne amintim formula unghiului dublu de la școală. Dar mai întâi să facem diferența:

,

(aceasta este formula unghiului dublu)