Tyrimo projektas „Paveikslėlio formulė languoto popieriaus geometrijoje. Piko formulė mokyklos planimetrijos kurse

Darbo tekstas skelbiamas be vaizdų ir formulių.
Pilna versija darbą galima rasti skirtuke „Darbo failai“ PDF formatu

Įvadas

Esu 6 klasės mokinė. Geometriją pradėjau studijuoti pernai, nes mokykloje mokausi pagal vadovėlį „Matematika. Aritmetika. Geometrija“, redagavo E.A. Bunimovičius, L.V. Kuznecova, S.S. Minaeva ir kt.

Daugiausia dėmesio sulaukė temos „Figūrų plotai“ ir „Formulių sudarymas“. Pastebėjau, kad galima rasti tų pačių figūrų plotus Skirtingi keliai. Kasdieniame gyvenime dažnai susiduriame su erdvės paieškos problema. Pavyzdžiui, suraskite grindų plotą, kurį reikės dažyti. Įdomu pirkti reikalinga suma tapetai renovacijai, reikia žinoti patalpos dydį, t.y. sienos plotas. Kvadrato, stačiakampio ir stačiakampio trikampio ploto apskaičiavimas man nesukėlė jokių sunkumų.

Susidomėjęs šia tema, pradėjau ieškoti papildomos medžiagos internete. Dėl savo paieškų radau Pick formulę - tai formulė, skirta apskaičiuoti daugiakampio plotą, nubrėžtą ant languoto popieriaus. Man atrodė, kad apskaičiuoti plotą pagal šią formulę gali bet kuris studentas. Todėl ir nusprendžiau diriguoti tiriamasis darbas.

Temos aktualumas:

Ši tema yra geometrijos kurso studijų papildymas ir pagilinimas.

Šios temos studijos padės geriau pasiruošti olimpiadoms ir egzaminams.

Darbo tikslas:

Susipažinkite su Peak formule.

Įvaldykite geometrinių uždavinių sprendimo būdus naudojant Pick formulę.

Sisteminti ir apibendrinti teorinę ir praktinę medžiagą.

Tyrimo tikslai:

Patikrinkite formulės naudojimo efektyvumą ir galimybes spręsdami problemas.

Išmokite taikyti Peak formulę įvairaus sudėtingumo problemoms spręsti.

Palyginkite problemas, išspręstas naudojant Pick formulę ir tradicinį metodą.

Pagrindinė dalis

1.1. Istorinė nuoroda

Georgas Aleksandras Piekas – austrų matematikas, gimęs 1859 m. rugpjūčio 10 d. Jis buvo gabus vaikas, jį mokė tėvas, kuris vadovavo privačiam institutui. Būdamas 16 metų Georgas baigė mokyklą ir įstojo į Vienos universitetą. Būdamas 20 metų jis gavo teisę dėstyti fiziką ir matematiką. Jo formulė daugiakampio tinklelio plotui nustatyti atnešė jam pasaulinę šlovę. Savo formulę jis paskelbė straipsnyje 1899 m. Jis išpopuliarėjo, kai lenkų mokslininkas Hugo Steinhausas įtraukė jį į 1969 m. matematinių momentinių nuotraukų leidinį.

Georgas Pieckas įgijo išsilavinimą Vienos universitete ir 1880 m. apgynė daktaro laipsnį. Gavęs daktaro laipsnį, jis buvo paskirtas Ernesto Macho asistentu Scherl-Ferdinando universitete Prahoje. Ten jis tapo mokytoju. Prahoje jis liko iki išėjimo į pensiją 1927 m., o paskui grįžo į Vieną.

Pickas pirmininkavo Vokietijos Prahos universiteto komitetui, kuris 1911 m. paskyrė Einšteiną matematinės fizikos katedros profesoriumi.

Jis buvo išrinktas Čekijos mokslų ir meno akademijos nariu, bet buvo pašalintas naciams užėmus Prahą.

Kai 1938 m. kovo 12 d. naciai įžengė į Austriją, jis grįžo į Prahą. 1939 metų kovą naciai įsiveržė į Čekoslovakiją. 1942 m. liepos 13 d. Pieckas buvo deportuotas į Theresienstadt stovyklą, nacių įkurtą Šiaurės Bohemijoje, kur po dviejų savaičių mirė sulaukęs 82 metų.

1.2. Tyrimai ir įrodymai

Savo tiriamąjį darbą pradėjau užduodamas klausimą: kokias figūrų sritis galiu rasti? Parašykite formulę plotui apskaičiuoti skirtingi trikampiai o keturkampius galėčiau. Bet kaip su penkių, šešių ir apskritai daugiakampiais?

Atlikdamas tyrimus įvairiose svetainėse mačiau problemų, susijusių su penkių, šešių ir kitų daugiakampių plotų skaičiavimu, sprendimus. Formulė, leidžianti išspręsti šias problemas, buvo vadinama Picko formule. Ji atrodo taip :S =B+G/2-1, Kur IN- daugiakampio viduje esančių mazgų skaičius, G- mazgų, esančių ant daugiakampio ribos, skaičius. Šios formulės ypatumas yra tas, kad ją galima naudoti tik daugiakampiams, nupieštiems ant languoto popieriaus.

Bet kurį tokį daugiakampį galima lengvai padalyti į trikampius su viršūnėmis gardelės mazguose ir neturinčių mazgų nei viduje, nei iš šonų. Galima parodyti, kad visų šių trikampių plotai yra vienodi ir lygūs ½, todėl daugiakampio plotas yra lygus pusei jų skaičiaus T.

Norėdami rasti šį skaičių, daugiakampio kraštinių skaičių pažymėkime n IN- jo viduje esančių mazgų skaičius G- mazgų skaičius šonuose, įskaitant viršūnes. visas kiekis visų trikampių kampai yra 180°. T.

Dabar suraskime sumą kitu būdu.

Kampų su viršūne bet kuriame vidiniame mazge suma lygi 2,180°, t.y. bendra kampų suma yra 360°. IN; bendra kampų suma mazgams šonuose, bet ne viršūnėse yra ( G-n)180°, o kampų suma daugiakampio viršūnėse bus lygi ( G-2)180°. Taigi, T = 2,180°. B+(G-n)180°+(n -2)180 °. Atidarę skliaustus ir padalydami iš 360°, gauname daugiakampio ploto S formulę, žinomą kaip Picko formulė.

2. Praktinė dalis

Nusprendžiau išbandyti šią formulę su užduotimis iš OGE-2017 kolekcijos. Apskaičiuojant trikampio, keturkampio ir penkiakampio plotą, iškilo problemų. Nusprendžiau palyginti atsakymus, spręsdamas dviem būdais: 1) papildžiau figūras iki stačiakampio ir iš gauto stačiakampio ploto atėmė stačiųjų trikampių plotą; 2) pritaikė Pick formulę.

S = 18-1,5-4,5 = 12 ir S = 7 + 12/2-1 = 12

S = 24-9-3 = 12 ir S = 7 + 12/2-1 = 12

S = 77-7,5-12-4,5-4 = 49 ir S = 43 + 14/2-1 = 49

Palyginęs rezultatus, darau išvadą, kad abi formulės duoda tą patį atsakymą. Figūros ploto radimas naudojant Picko formulę pasirodė greitesnis ir lengvesnis, nes buvo mažiau skaičiavimų. Sprendimo paprastumas ir skaičiavimams skirto laiko taupymas man bus naudingas ateityje atliekant OGE.

Tai paskatino mane patikrinti galimybę pritaikyti Pick formulę sudėtingesnėms figūroms.

S = 0 + 4/2 -1 = 1

S = 5+11/2-1 = 9,5

S = 4+16/2-1 = 1

Išvada

Peak formulė yra lengvai suprantama ir paprasta naudoti. Pirma, pakanka mokėti skaičiuoti, padalyti iš 2, sudėti ir atimti. Antra, jūs galite rasti sudėtingos figūros plotą nepraleisdami daug laiko. Trečia, ši formulė tinka bet kokiam daugiakampiui.

Trūkumas yra tas, kad rinkimo formulė taikoma tik figūroms, kurios yra nupieštos ant languoto popieriaus ir kurių viršūnės yra ant languoto popieriaus mazgų.

Esu tikras, kad išlaikant baigiamuosius egzaminus figūrų ploto skaičiavimo problemos nesukels sunkumų. Juk aš jau susipažinau su Peak formule.

Bibliografija

Bunimovičius E.A., Dorofejevas G.V., Suvorova S.B. ir kt.. Matematika. Aritmetika. Geometrija. 5 klasė: mokomoji. bendrajam lavinimui organizacijos su adj. vienam elektronui vežėjas - 3 leidimas - M.: Išsilavinimas, 2014.- 223, p. : nesveikas. - (Sferos).

Bunimovičius E.A., Kuznecova L.V., Minaeva S.S. ir kt.. Matematika. Aritmetika. Geometrija. 6 klasė: mokomoji. bendrajam lavinimui organizacijos-5 leid.-M.: Švietimas, 2016.-240 p. : lig.- (Sferos).

Vasiljevas N.B. Aplink Pick formulę. //Kvant.- 1974.-Nr.2. -p.39-43

Rassolovas V.V. Planimetrijos problemos. / 5-asis leidimas, red. Ir papildomai - M.: 2006.-640s.

I.V. Jaščenka. OGE. Matematika: standartiniai egzamino variantai: O-39 36 variantai - M.: Leidykla " Tautinis švietimas“, 2017. -240 p. - (OGE. FIPI-mokykla).

„Aš išspręsiu OGE“: matematika. Dmitrijaus Guščino mokymo sistema. OGE-2017: užduotys, atsakymai, sprendimai [Elektroninis išteklius]. Prieigos režimas: https://oge.sdamgia.ru/test?id=6846966 (prieigos data 2017-02-04)

Naudodami Picko formulę galite rasti ant popieriaus lapo sukonstruotos figūros plotą narve (trikampis, kvadratas, trapecija, stačiakampis, daugiakampis).

Užduotyse, kurios bus vieningame valstybiniame egzamine, yra visa grupė užduočių, kuriose pateikiamas daugiakampis, sukonstruotas ant popieriaus lapo kvadrate ir klausimas yra apie ploto radimą. Ląstelės dydis yra vienas kvadratinis centimetras.

Peržiūrėkite pristatymo turinį

Georgas Pickas

Georgas Aleksandras Pickas,

austrų matematikas

(10.08.1859 - 13.07.1942)

Formulė buvo atrasta 1899 m.

Norimos figūros plotą galima rasti pagal formulę:

M – mazgų skaičius trikampio kraštinėje (šoninėse ir viršūnėse):
N – mazgų skaičius trikampio viduje;

* „Mazgai“ turime omenyje linijų sankirtą.

Raskime trikampio plotą:

Pažymime mazgus:

1 langelis = 1 cm

M = 15 (pažymėta raudona spalva)
N = 34 (mėlyna)

Raskime lygiagretainio plotą:

Pažymime mazgus:

M = 18 (pažymėta raudona spalva)
N = 20 (mėlyna spalva)

Raskime trapecijos plotą:

Pažymime mazgus:

M = 24 (pažymėta raudona spalva)
N = 25 (mėlyna)

Raskime daugiakampio plotą:

Pažymime mazgus:

M = 14 (pažymėta raudona spalva)
N = 43 (mėlyna)

Pažymime mazgus:

M = 11 (pažymėta raudona spalva)
N = 5 (mėlyna spalva)

Spręskite patys:

1. Raskite ant languoto popieriaus pavaizduoto keturkampio plotą, kurio langelio dydis 1 cm x 1 cm. Atsakymą pateikite kvadratiniais centimetrais.

4. Raskite ant languoto popieriaus pavaizduoto keturkampio plotą, kurio langelio dydis 1 cm x 1 cm. Atsakymą pateikite kvadratiniais centimetrais .

Aplink jį nubrėžkime stačiakampį:

Iš stačiakampio ploto (in tokiu atveju tai yra kvadratas) atimkite gautų paprastų figūrų plotus:

Atsakymai:

№ užduotys

1 variantas

2 variantas

3 variantas

4 variantas

Pasirinkite formulę

Sazhina Valeria Andreevna, MAOU "Vidurinės mokyklos Nr. 11" 9 klasės mokinys Ust-Ilimske, Irkutsko srityje

Prižiūrėtojas: Gubaras Oksana Michailovna, aukščiausios kvalifikacinės kategorijos matematikos mokytojas, MAOU "Vidurinė mokykla Nr. 11", Ust-Ilimsk, Irkutsko sritis

2016 m

Įvadas

Studijuodamas geometrijos temą „Daugiakampių sritys“ nusprendžiau išsiaiškinti: ar yra būdas rasti sritis, kurios skiriasi nuo tų, kurias mokėmės klasėje?

Šis metodas yra Pick formulė. L.V.Gorina „Mokinių saviugdos medžiagoje“ šią formulę apibūdino taip: „Supažindinimas su Peak formule yra ypač svarbus dieną prieš išlaikęs vieningą valstybinį egzaminą ir GIA. Naudodami šią formulę galite nesunkiai išspręsti didelę egzaminuose siūlomų uždavinių klasę – tai daugiakampio ploto, pavaizduoto ant languoto popieriaus, paieškos problemos. Pick mažoji formulė pakeis visą formulių rinkinį, reikalingą tokioms problemoms išspręsti. Peak formulė veiks „vienas už visus...“!

Vieningo valstybinio egzamino medžiagoje susidūriau su praktinio turinio problemomis ieškant žemės sklypų ploto. Nusprendžiau patikrinti, ar ši formulė tinka ieškant mokyklos teritorijos ploto, miesto mikrorajonų, regiono. Ir ar racionalu jį naudoti sprendžiant problemas?

Tyrimo objektas: Picko formulė.

Tyrimo objektas: racionalus Pick formulės taikymas sprendžiant problemas.

Darbo tikslas: pagrįsti Pick formulės naudojimo racionalumą sprendžiant languotame popieriuje pavaizduotų figūrų ploto radimo uždavinius.

Tyrimo metodai: modeliavimas, palyginimas, apibendrinimas, analogijos, literatūros ir interneto išteklių tyrimas, informacijos analizė ir klasifikavimas.

Pasirinkti reikiamą literatūrą, analizuoti ir sisteminti gautą informaciją;

Apsvarstykite įvairių metodų ir uždavinių sprendimo ant languoto popieriaus technikas;

Patikrinti eksperimentiškai Pick formulės naudojimo racionalumas;

Apsvarstykite šios formulės taikymą.

Hipotezė: jei daugiakampio plotui rasti pritaikysite Picko formulę, galėsite rasti teritorijos plotą, o uždavinių sprendimas languotame popieriuje bus racionalesnis.

Pagrindinė dalis

Teorinė dalis

Languotas popierius (tiksliau, jo mazgai), ant kurio dažnai mieliau piešiame ir piešime, yra vienas svarbiausių taškinės gardelės plokštumoje pavyzdžių. Jau ši paprasta gardelė pasitarnavo kaip atskaitos taškas K. Gaussui lyginant apskritimo plotą su taškų su sveikųjų skaičių koordinatėmis, esančių jos viduje, skaičiumi. Tai, kad kai kurie paprasti geometriniai teiginiai apie figūras plokštumoje turi gilių pasekmių aritmetiniams tyrimams, G. Minkovskis aiškiai pastebėjo 1896 m., kai pirmą kartą panaudojo geometrinius metodus nagrinėdamas skaičių teorines problemas.

Ant languoto popieriaus nubrėžkime kokį nors daugiakampį (1 priedas, 1 pav.). Dabar pabandykime apskaičiuoti jo plotą. Kaip tai padaryti? Turbūt lengviausia jį padalinti į stačiuosius trikampius ir trapeciją, kurių plotus nesunku apskaičiuoti ir susumuoti rezultatus.

Naudojamas metodas yra paprastas, bet labai sudėtingas, be to, jis tinka ne visiems daugiakampiams. Taigi kito daugiakampio negalima skaidyti į stačiuosius trikampius, kaip tai padarėme ankstesniu atveju (2 priedas, 2 pav.). Galime, pavyzdžiui, pabandyti jį papildyti iki mums reikalingo „gerojo“, tai yra, kurio plotą galime apskaičiuoti aprašytu būdu, tada iš gauto skaičiaus atimti pridėtų dalių plotus.

Tačiau pasirodo, kad yra labai paprasta formulė, leidžianti apskaičiuoti tokių daugiakampių, kurių viršūnės yra kvadratinio tinklelio mazguose, plotus.

Šią formulę 1899 m. atrado austrų matematikas Peakas Georgas Aleksandrovas (1859 - 1943). Be šios formulės, Georgas Pickas atrado Pick, Pick-Julia, Pick-Nevalina teoremas ir įrodė Schwartz-Pick nelygybę.

Ši formulė kurį laiką liko nepastebėta po to, kai Pickas ją paskelbė, tačiau 1949 metais lenkų matematikas Hugo Steinhausas įtraukė teoremą į savo garsųjį „Matematinį kaleidoskopą“. Nuo to laiko Picko teorema tapo plačiai žinoma. Vokietijoje Picko formulė įtraukta į mokyklinius vadovėlius.

Tai klasikinis kombinatorinės geometrijos ir skaičių geometrijos rezultatas.

Picko formulės įrodymas

Tegul ABCD yra stačiakampis, kurio viršūnės mazguose ir kraštinės eina išilgai tinklelio linijų (3 priedas, 3 pav.).

B pažymėkime stačiakampio viduje esančių mazgų skaičių, o G – mazgų skaičių jo kraštinėje. Perkelkime tinklelį pusę langelio į dešinę ir pusę langelio

žemyn. Tada stačiakampio teritoriją galima „paskirstyti“ tarp mazgų taip: kiekvienas B mazgas „valdo“ visą perkelto tinklelio langelį, o kiekvienas G mazgas valdo 4 kraštinius ne kampinius mazgus – pusę langelio. , o kiekvienas kampinis taškas valdo ketvirtadalį langelio. Todėl stačiakampio S plotas lygus

S = B + + 4 · = B + - 1 .

Taigi, stačiakampiams, kurių viršūnės yra mazguose ir šonuose išilgai tinklelio linijų, nustatėme formulę S = B + - 1 . Tai yra Peak formulė.

Pasirodo, ši formulė tinka ne tik stačiakampiams, bet ir savavališkiems daugiakampiams su viršūnėmis tinklelio mazguose.

Praktinė dalis

Figūrų ploto radimas naudojant geometrinį metodą ir naudojant Pick formulę

Nusprendžiau įsitikinti, kad Pick formulė buvo teisinga visiems nagrinėjamiems pavyzdžiams.

Pasirodo, jei daugiakampis gali būti supjaustytas į trikampius, kurių viršūnės yra tinklelio mazguose, tada Pick formulė jam tinka.

Pažiūrėjau kai kurias problemas ant languoto popieriaus su 1 cm1 cm kvadratėliais ir atlikau lyginamoji analizė dėl problemų sprendimo (lentelė Nr. 1).

Lentelė Nr. 1 Užduočių sprendimas įvairiais būdais.

Piešimas

Pagal geometrijos formulę

Pagal Picko formulę

Užduotis Nr.1

S = S ir tt -(2S 1 +2S 2 )

S ir tt =4*5=20 cm 2

S 1 =(2*1)/2=1 cm 2

S 2 =(2*4)/2=4 cm 2

S=20-(2*1+2*4)=10 cm 2

Atsakymas :10 cm ².

B = 8, D = 6

S= 8 + 6/2 – 1 = 10 (cm²)

Atsakymas: 10 cm².

2 užduotis

a = 2, h = 4

S=a*h=2*4=8 cm 2

Atsakymas : 8 cm ².

B = 6, D = 6

S= 6 + 6/2 – 1 = 8 (cm²)

Atsakymas: 8 cm².

Užduotis Nr.3

S = S kv -(S 1 +2S 2 )

S kv =4 2 =16 cm 2

S 1 = (3 * 3) / 2 = 4,5 cm 2

S 2 = (1 * 4) / 2 = 2 cm 2

S=16-(4,5+2*2)=7,5 cm2

B = 6, D = 5

S= 6 + 5/2 – 1 = 7,5 (cm²)

Atsakymas: 7,5 cm².

4 užduotis

S = S ir tt -(S 1 +S 2+ S 3 )

S ir tt =4 * 3=12 cm 2

S 1 =(3*1)/2=1,5 cm 2

S 2 =(1*2)/2=1 cm 2

S 3 =(1+3)*1/2=2 cm 2

S=12-(1,5+1+2)=7,5 cm 2

B = 5, D = 7

S= 5 + 7/2 – 1 = 7,5 (cm²)

Atsakymas: 7,5 cm².

Užduotis Nr. 5.

S = S ir tt -(S 1 +S 2+ S 3 )

S ir tt =6 * 5=30 cm 2

S 1 =(2*5)/2=5 cm 2

S 2 =(1*6)/2=3 cm 2

S 3 =(4*4)/2=8 cm 2

S=30-(5+3+8)=14 cm 2

Atsakymas: 14 cm²

B = 12, D = 6

S= 12 + 6/2 – 1 = 14 (cm²)

Atsakymas: 14 cm²

Užduotis №6.

S tr =(4+9)/2*3=19,5 cm2

Atsakymas: 19,5 cm 2

H = 12, D = 17

S= 12 + 17/2 – 1 = 19,5 (cm²)

Atsakymas: 19,5 cm 2

Užduotis №7. Raskite miško plotą (m²), pavaizduotą plane su 1 × 1 (cm) kvadratine tinkleliu 1 cm - 200 m skalėje

S = S 1 +S 2+ S 3

S 1 =(800*200)/2=80000 m 2

S 2 =(200*600)/2=60000 m 2

S 3 =(800+600)/2*400=

280000 m 2

S = 80000+60000+240000=

420 000 m 2

Atsakymas: 420 000 m²

B = 8, D = 7. S= 8 + 7/2 – 1 = 10,5 (cm²)

1 cm² - 200² m²; S= 40 000 10,5 = 420 000 (m²)

Atsakymas: 420 000 m²

Problema Nr.8 . Raskite lauko plotą (m²), parodytą plane su 1 × 1 (cm) kvadratine tinkleliu pagal mastelį

1 cm – 200 m.

S= S kv -2( S tr + S kopėčios)

S kv = 800 * 800 = 640 000 m 2

S tr =(200*600)/2=60000m 2

S kopėčios =(200+800)/2*200=

100 000 m2

S=640000-2(60000+10000)=

320000 m2

Atsakymas: 320 000 m²

Sprendimas. Raskime Sketurkampio plotas, nupieštas ant languoto popieriaus, naudojant Picko formulę:S= B + - 1

B = 7, D = 4. S= 7 + 4/2 – 1 = 8 (cm²)

1 cm² - 200² m²; S= 40 000 8 = 320 000 (m²)

Atsakymas: 320 000 m²

Problema Nr.9 . Raskite sritįS sektoriuje, atsižvelgiant į kvadratinių langelių kraštines lygias 1. Savo atsakyme nurodykite .

Sektorius sudaro vieną ketvirtadalį apskritimo, todėl jo plotas yra ketvirtadalis apskritimo ploto. Apskritimo plotas yra πR 2 , Kur R – apskritimo spindulys. Mūsų atvejuR =√5 taigi ir sritisS sektorius yra 5π/4. KurS/π=1,25.

Atsakymas. 1.25.

Г = 5, В = 2, S= V + G/2 – 1 = 2 + 5/2 – 1 = 3,5, ≈ 1,11

Atsakymas. 1.11.

10 užduotis. Raskite sritį S žiedai, atsižvelgiant į kvadratinių langelių kraštines lygias 1. Savo atsakyme nurodykite .

Žiedo plotas lygus skirtumui tarp išorinio ir vidinio apskritimų plotų. SpindulysR išorinis apskritimas yra lygus

2 , spindulys r vidinis apskritimas yra 2. Todėl žiedo plotas yra 4ir todėl. Atsakymas: 4.

G = 8, B = 8, S= V + G/2 – 1 = 8 + 8/2 – 1 = 11, ≈ 3,5

Atsakymas: 3.5

Išvados: Nagrinėjamos užduotys yra panašios į užduotį iš valdymo ir matavimo parinkčių Vieningo valstybinio egzamino medžiaga matematikoje (uždaviniai Nr. 5,6),.

Iš svarstytų problemų sprendimo būdų pamačiau, kad kai kurias iš jų, pavyzdžiui, uždavinius Nr. 2.6, lengviau išspręsti naudojant geometrines formules, nes aukštį ir pagrindą galima nustatyti pagal brėžinį. Tačiau dauguma užduočių reikalauja išskaidyti figūrą į paprastesnes (užduotis Nr. 7) arba sukonstruoti iki stačiakampio (užduotys Nr. 1,4,5), kvadrato (užduotis Nr. 3,8).

Spręsdamas uždavinius Nr.9 ir Nr.10 pamačiau, kad pritaikius Pick formulę figūroms, kurios nėra daugiakampiai, gaunamas apytikslis rezultatas.

Siekdamas patikrinti Peak formulės naudojimo racionalumą, atlikau sugaišto laiko tyrimą (4 priedas, lentelė Nr. 2).

Išvada: iš lentelės ir diagramos (4 priedas, diagrama 1) aišku, kad sprendžiant uždavinius naudojant Peak formulę, sugaištama daug mažiau laiko.

Erdvinių formų paviršiaus ploto radimas

Patikrinkime šios formulės pritaikymą erdvinėms formoms (5 priedas, 4 pav.).

Rasti sritį viso paviršiaus stačiakampis gretasienis, atsižvelgiant į kvadratinių langelių kraštines, lygias 1.

Tai yra formulės trūkumas.

Peak formulės taikymas norint rasti teritorijos plotą

Spręsdamas praktinio turinio problemas (uždaviniai Nr. 7,8; lentelė Nr. 1), nusprendžiau šiuo metodu rasti mūsų mokyklos teritorijos plotą, Ust-Ilimsko miesto mikrorajonus, Irkutską. regione.

Susipažinęs su „Ust-Ilimsko žemės sklypo MAOUSOSH Nr. 11 ribų projektu“ (6 priedas), radau mūsų mokyklos teritorijos plotą ir palyginau jį su plotu pagal žemės sklypo projekto ribos (9 priedas, 3 lentelė).

Išnagrinėjęs Ust-Ilimsko dešiniojo kranto dalies žemėlapį (7 priedas), apskaičiavau mikrorajonų plotus ir palyginau juos su „Irkutsko srities Ust-Ilimsko bendrojo plano“ duomenimis. Rezultatai pateikti lentelėje (9 priedas, 4 lentelė).

Išnagrinėjęs Irkutsko srities žemėlapį (7 priedas), radau teritorijos plotą ir palyginau jį su Vikipedijos duomenimis. Rezultatai pateikti lentelėje (9 priedas, 5 lentelė).

Išanalizavęs rezultatus padariau išvadą: naudojant Peak formulę šias sritis galima rasti daug lengviau, tačiau rezultatai yra apytiksliai.

Iš atliktų tyrimų gavau tiksliausią reikšmę nustatant mokyklos teritorijos plotą (10 priedas, 2 diagrama). Didesnis rezultatų neatitikimas gautas ieškant Irkutsko srities teritorijos (10 priedas, 3 diagrama). Tai susiję su tuo. Kad ne visos ploto ribos yra daugiakampių kraštinės, o viršūnės nėra mazgo taškai.

Išvada

Dėl savo darbo praplėčiau žinias apie uždavinių sprendimą languotame popieriuje ir pati nusprendžiau tiriamų problemų klasifikaciją.

Darbo metu buvo išspręstos uždaviniai, kaip rasti daugiakampių plotą, pavaizduotą ant languoto popieriaus dviem būdais: geometriniu ir naudojant Pick formulę.

Sprendimų analizė ir eksperimentas sugaištam laikui nustatyti parodė, kad formulės naudojimas leidžia racionaliau išspręsti daugiakampio ploto nustatymo problemas. Tai leidžia sutaupyti laiko vieningam valstybiniam matematikos egzaminui.

Įvairių figūrų, pavaizduotų languotame popieriuje, ploto radimas leido daryti išvadą, kad naudoti Pick formulę apskrito sektoriaus ir žiedo plotui apskaičiuoti yra netikslinga, nes taip gaunamas apytikslis rezultatas, o Pick formulė nėra tinkama. naudojamas kosmoso problemoms spręsti.

Darbe taip pat buvo rasti įvairių teritorijų plotai, naudojant Peak formulę. Galime daryti išvadą: naudojant formulę galima rasti įvairių teritorijų plotą, tačiau rezultatai yra apytiksliai.

Mano iškelta hipotezė pasitvirtino.

Padariau išvadą, kad mane dominusi tema gana įvairiapusė, uždaviniai languotame popieriuje – įvairūs, jų sprendimo būdai ir būdai taip pat įvairūs. Todėl nusprendžiau ir toliau dirbti šia kryptimi.

Literatūra

Volkovas S.D.. Žemės ribų projektas, 2008, p. 16.

Gorina L.V., Matematika. Viskas mokytojui, M:Nauka, 2013. Nr.3, p. 28.

Prokopjeva V.P., Petrovas A.G., Ust-Ilimsko miesto bendrasis planas, Irkutsko sritis, Rusijos Gosstroy, 2004. p. 65.

Riess E. A., Žarkovskaja N. M., Languoto popieriaus geometrija. Peako formulė. - Maskva, 2009, Nr. 17, p. 24-25.

Smirnova I. M. ,. Smirnovas V. A. Geometrija ant languoto popieriaus. – Maskva, Chistye Prudy, 2009, p. 120.

Smirnova I. M., Smirnov V. A., Geometrinės problemos su praktiniu turiniu. – Maskva, Chistye Prudy, 2010, p. 150

Matematikos atvirojo užduočių banko problemos FIPI, 2015 m.

Ust-Ilimsko miesto žemėlapis.

Irkutsko srities žemėlapis.

Vikipedija.

Pasirinkite formulę

1. Įvadas

2. Piko formulė. I paroda.

II įrodymas.

Įrodymas Sh.

3. Tikslai.

4. Daugiakampio ploto formulė, naudojant viršūnių koordinates.

5. Užduotys.

6. Literatūra

Peako formulė.

1. Įvadas.

Mes semiamės išminties iš istorijos,

poezijoje - sąmojis,

matematikoje – įžvalga.

F. Bekonas

Siužetas klostysis ant paprasto languoto popieriaus lapo.

Linijos, einančios išilgai langelių šonų, sudaro tinklelį, o langelių viršūnės yra šio tinklelio mazgai. Nubraižykime ant lapo daugiakampį su viršūnėmis mazguose ir raskime jo plotą.

Galite jo ieškoti įvairiais būdais. Pavyzdžiui, galite iškirpti daugiakampį pakankamai paprastos figūros, suraskite jų sritis ir sudėkite jas.

Bet čia mūsų laukia daug rūpesčių. Figūra lengvai suskirstoma į stačiakampius, trapecijas ir trikampius, o jos plotas apskaičiuojamas be pastangų.

Nors daugiakampis atrodo pakankamai paprastas, jo ploto apskaičiavimas reikalauja daug darbo. O jei daugiakampis atrodytų puošnesnis? Pasirodo, daugiakampių, kurių viršūnės yra tinklelio mazguose, plotus galima apskaičiuoti daug paprasčiau: yra formulė, susiejanti jų plotą su mazgų, esančių daugiakampio viduje ir ant ribos, skaičiumi. Ši nuostabi ir paprasta formulė vadinama Pick formule.

2. Piko formulė.

Daugiakampio viršūnės (nebūtinai išgaubtos) yra sveikosios gardelės mazguose. Jo viduje yra B gardelės mazgai, o ant ribos yra G mazgai. Įrodykime, kad jo plotas lygus B + – 1 (Pasirinkti formulę).

I paroda.

Panagrinėkime daugiakampį, kurio viršūnės yra sveikosios gardelės mazguose, tai yra, jos turi sveikąsias koordinates.

Daugiakampį padalijame į trikampius, kurių viršūnės yra gardelės mazguose, kuriose nėra mazgų nei viduje, nei iš šonų.

Pažymime:

n– daugiakampio kraštinių skaičius,

m– trikampių su viršūnėmis gardelės mazguose, kuriuose nėra mazgų nei viduje, nei iš šonų, skaičius,

B – mazgų skaičius daugiakampyje,

Г – mazgų skaičius šonuose, įskaitant viršūnes.

Visų šių trikampių plotai yra vienodi ir lygūs.

Todėl daugiakampio plotas yra
.

180 0 m .

Dabar suraskime šią sumą kitu būdu.

Kampų su viršūne bet kuriame vidiniame mazge suma yra 360 0.

Tada kampų su viršūnėmis visuose vidiniuose mazguose suma lygi 360 0 V.

Bendra kampų suma mazgams šonuose, bet ne viršūnėse, yra 180 0 (G - n).

Daugiakampio viršūnių kampų suma yra 180 0 ( n – 2) .

Bendra visų trikampių kampų suma yra 360 0 V + 180 0 (G – n) + 180 0 (n – 2).

Taigi 180 0 m= 360 0 V + 180 0 (G – n) + 180 0 (n – 2),

180 0 m= 360 0 V + 180 0 G – 180 0 n + 180 0 n– 180 0 2,

180 0 m= 360 0 V + 180 0 G – 360 0,

= B + – 1 ,

iš kurios gauname daugiakampio ploto S išraišką:

S= B + – 1 ,

žinoma kaip Picko formulė.

Paveiksle: B = 24, D = 9, todėlS = 24 + – 1 = 27,5.

Raskime pirmojo daugiakampio plotą naudodami Peak formulę:

B = 28 (žali taškai);

G = 20 (mėlyni taškai).

Mes gauname, S =
= 37 kv

II įrodymas.

Kiekvienam daugiakampiui M, kurio viršūnės yra sveikosios gardelės mazguose, priskiriame skaičių f (M) =
, kur sumavimas atliekamas per visus gardelės mazgus, priklausančius M, ir kampą apibrėžiamas taip: =
daugiakampio vidiniam taškui, =
ribiniam taškui, kuris nėra viršūnė, ir – viršūnės kampas, jei šis mazgas yra viršūnė. Nesunku pastebėti, kad f(M) =
+
= B + – 1. Belieka patikrinti, ar skaičius f (M) yra lygus daugiakampio M plotui.

Daugiakampis M supjaustomas į daugiakampius M 1 ir M 2 su viršūnėmis gardelės mazguose. Tada f (M) = f (M 1) + f (M 2), nes kiekvienam mazgui pridedami kampai. Todėl, jei Picko formulė yra teisinga dviem daugiakampiams M, M 1 ir M 2, tai ji tinka ir trečiajam.

Jei M yra stačiakampis su kraštinėmis p Ir q, nukreiptas išilgai gardelės linijų, tada

f (M) = (p – 1) (q – 1) +
= pq.

Šiuo atveju galioja Peako formulė. Iškirpus stačiakampį M su įstriža į trikampius M 1 ir M 2 ir panaudojus faktą, kad f (M) = f (M 1) + f (M 2) ir f (M 1) = f (M 2), lengva įrodyti Pick formulės pagrįstumą bet kokiam stačiajam trikampiui, kurio kojos nukreiptos išilgai gardelės linijų. Iškirpę kelis iš šių trikampių iš stačiakampio, galite gauti bet kurį trikampį.

Norint užbaigti Picko formulės įrodymą, belieka pažymėti, kad bet kurį daugiakampį galima išpjauti į trikampius atskirtomis įstrižainėmis.

Įrodymas Sh.

Ryšys tarp figūros ploto ir į šią figūrą įtrauktų mazgų skaičiaus ypač aiškiai matomas stačiakampio atveju.

Leisti ABCD- stačiakampis, kurio viršūnės mazguose ir šonuose eina išilgai tinklelio linijų.

Pažymėkime pagal IN mazgų, esančių stačiakampio viduje, skaičius ir per jį G- mazgų skaičius ant jo ribos. Perkelkime tinklelį puse langelio į dešinę ir puse langelio žemyn.

Tada stačiakampio teritoriją galima „paskirstyti“ tarp mazgų taip: kiekvienas iš IN mazgai „valdo“ visą perkelto tinklelio langelį, kiekvieną iš jų G– 4 kraštiniai nekampiniai mazgai yra pusė langelio, o kiekvienas kampinis taškas yra ketvirtadalis langelio. Todėl stačiakampio S plotas lygus

Taigi, stačiakampiams su viršūnėmis mazguose ir šonuose išilgai tinklelio linijų sukūrėme formulę

Įrodykime, kad ši formulė tinka ne tik stačiakampiams, bet ir savavališkiems daugiakampiams su viršūnėmis tinklelio mazguose.

Pažymėkime pagal S m daugiakampio plotasM su viršūnėmis mazguose ir perP m – dydis
, KurIN m – viduje esančių mazgų skaičiusM, A G m - mazgų skaičius pasienyje. Tada Peako formulę galima parašyti kaip
.

Formulės įrodymą suskirstysime į kelis veiksmus.

1 žingsnis.

Jei daugiakampisM su viršūnėmis ties tinklo mazgais, supjaustytais į 2 daugiakampiusM 1 Ir M 2 , taip pat turinčios viršūnes tik tinklelio mazguose, tada
. Tegul daugiakampisM supjaustyti daugiakampiaisM 1 Ir M 2 su viršūnėmis mazguose pagal segmentą AB. Visi mazgai, išskyrus tuos, kurie patenka į segmentąAB, vienodai įneša į kairę ir dešinę formulės puses. Panagrinėkime mazgus, esančius atkarpoje AB.

Jei toks mazgas yra tarp A ir B (pavyzdžiui, C), tada daugiakampiuiM jis yra vidinis, o daugiakampiamsM 1 Ir M 2 – ribinė. Todėl jo indėlis įP m yra lygus 1, ir kiekvienoje iš išraiškų
Ir
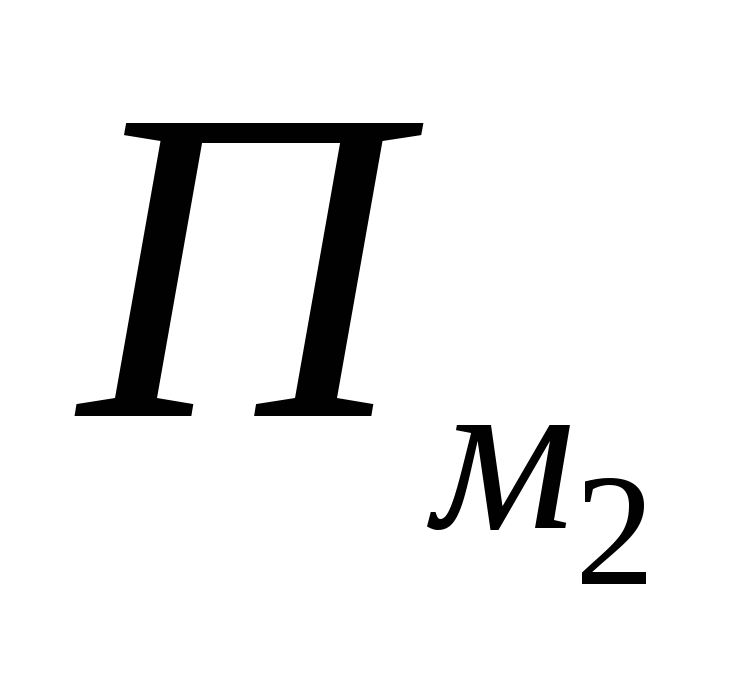– po 0,5, tai yra tokio mazgo įnašai įP m Ir
yra lygūs.

Panagrinėkime mazgus A ir B. Jie yra abiejų ribiniai mazgai M, ir už M 1 , M 2 .

Todėl kiekvieno iš šių mazgų indėlis įP m lygus 0,5 a colio
- vienetas. Tai reiškia, kad bendras mazgų A ir B indėlis įP m yra lygus 1, tai yra 1 mažiau nei jų indėlis į
. Bet
, A.

Nuo bendro visų mazgų „indėlio“. P m 1 atimamas ir iš
2 atimamas ir tai kompensuoja mazgų A ir B įnašų skirtumą.

Taigi,
.

2 žingsnis.

Jei daugiakampis M kurių viršūnės ties tinklo mazgais išpjautos į du daugiakampius M 1 Ir M 2 (taip pat su viršūnėmis mazguose) ir formulė yra teisinga kai kuriems dviem daugiakampiams MM 1 , M 2 , tada tai galioja ir trečiajam daugiakampiui.

Pavyzdžiui, tegul tai yra tiesaM 1 Ir M 2 , tai yra
. Tada (pirmu žingsniu), bet toliau pirmas žingsnis) paskutinė išraiška yra lygiP m , ir lygybė
ir yra Peak formulė.

3 veiksmas.

Įrodykime Peako formulę stačiajam trikampiui, kurio viršūnės yra tinklelio mazguose ir kojos, esančios tinklelio linijose.

Trikampis ABC pastatykite jį į stačiakampį ABCD .

Stačiakampiams Picko formulė yra teisinga: S ABCD = P ABCD . Pagal pirmąjį žingsnį P ABCD = P ABC + P ACD , P ABC = P ACD , Taigi P ABCD = 2P ABC . Bet S ABCD = 2 S ABC . Štai kodėl S ABC = P ABC .

4 veiksmas.

Picko formulė galioja savavališkam trikampiui su viršūnėmis tinklelio mazguose.

Ištyrus figūrą, nesunku suprasti: bet kurį tokį trikampį galima gauti „nupjovus“ iš tam tikro stačiakampio, kurio kraštinės yra išilgai tinklelio linijų, kelis stačiakampius ir stačiakampius su kojomis tinklelio linijose. Ir kadangi Picko formulė tinka stačiakampiams ir stačiakampiams trikampiams, tada (atminkite 2 veiksmą) ji tinka ir pradiniam trikampiui.

Mes įrodėme, kad jei daugiakampis gali būti supjaustytas į trikampius, kurių viršūnės yra tinklelio mazguose, tada Peak formulė yra teisinga.

3. Tikslai.

Raskite figūrų plotą:

1
.