Formule pentru găsirea ecuației unei tangente înclinate. Calculator online. Ecuația unei tangente drepte la graficul unei funcții într-un punct dat

Articolul oferă o explicație detaliată a definițiilor, semnificația geometrică a derivatului cu simboluri grafice. Ecuația unei linii tangente va fi luată în considerare cu exemple, se vor găsi ecuațiile unei tangente la curbele de ordinul 2.

Yandex.RTB R-A-339285-1 Definiție 1

Unghiul de înclinare al dreptei y = k x + b se numește unghi α, care se măsoară de la direcția pozitivă a axei x la dreapta y = k x + b în direcția pozitivă.

În figură, direcția x este indicată printr-o săgeată verde și un arc verde, iar unghiul de înclinare printr-un arc roșu. Linia albastră se referă la linia dreaptă.

Definiția 2

Panta dreptei y = k x + b se numește coeficient numeric k.

Coeficientul unghiular este egal cu tangentei dreptei, cu alte cuvinte k = t g α.

• Unghiul de înclinare al unei drepte este egal cu 0 numai dacă este paralelă în jurul lui x și panta este egală cu zero, deoarece tangenta lui zero este egală cu 0. Aceasta înseamnă că forma ecuației va fi y = b.
• Dacă unghiul de înclinare al dreptei y = k x + b este acut, atunci condițiile 0 sunt îndeplinite< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0 și există o creștere a graficului.
• Dacă α = π 2, atunci locația dreptei este perpendiculară pe x. Egalitatea este specificată de x = c, valoarea c fiind un număr real.
• Dacă unghiul de înclinare al dreptei y = k x + b este obtuz, atunci corespunde condițiilor π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

Definiția 3

O secantă este o dreaptă care trece prin 2 puncte ale funcției f (x). Cu alte cuvinte, o secanta este o linie dreaptă care este trasată prin oricare două puncte de pe grafic funcţie dată.

Figura arată că A B este o secante, iar f (x) este o curbă neagră, α este un arc roșu, indicând unghiul de înclinare al secantei.

Când pantă linia dreaptă este egală cu tangentei unghiului de înclinare, este clar că tangenta dintr-un triunghi dreptunghic A B C poate fi găsită prin raportul laturii opuse față de cea adiacentă.

Definiția 4

Obținem o formulă pentru găsirea unei secante de forma:

k = t g α = B C A C = f (x B) - f x A x B - x A, unde abscisele punctelor A și B sunt valorile x A, x B și f (x A), f (x B) sunt funcțiile de valori în aceste puncte.

Evident, coeficientul unghiular al secantei este determinat folosind egalitatea k = f (x B) - f (x A) x B - x A sau k = f (x A) - f (x B) x A - x B , iar ecuația trebuie scrisă ca y = f (x B) - f (x A) x B - x A x - x A + f (x A) sau
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .

Secanta împarte graficul vizual în 3 părți: la stânga punctului A, de la A la B, la dreapta lui B. Figura de mai jos arată că există trei secante care sunt considerate coincidente, adică sunt stabilite folosind un ecuație similară.

Prin definiție, este clar că o linie dreaptă și secanta ei în în acest caz, se potrivesc.

O secanta poate intersecta graficul unei funcții date de mai multe ori. Dacă există o ecuație de forma y = 0 pentru o secantă, atunci numărul de puncte de intersecție cu sinusoida este infinit.

Definiția 5

Tangenta la graficul functiei f (x) in punctul x 0 ; f (x 0) este o dreaptă care trece printr-un punct dat x 0; f (x 0), cu prezența unui segment care are multe valori x apropiate de x 0.

Exemplul 1

Să aruncăm o privire mai atentă la exemplul de mai jos. Atunci este clar că linia definită de funcția y = x + 1 este considerată tangentă la y = 2 x în punctul cu coordonatele (1; 2). Pentru claritate, este necesar să luați în considerare graficele cu valori apropiate de (1; 2). Funcția y = 2 x este afișată cu negru, linia albastră este linia tangentă, iar punctul roșu este punctul de intersecție.

Evident, y = 2 x se îmbină cu linia y = x + 1.

Pentru a determina tangentei, ar trebui să luăm în considerare comportamentul tangentei A B pe măsură ce punctul B se apropie la infinit de punctul A. Pentru claritate, prezentăm un desen.

Secanta A B, indicată de linia albastră, tinde spre poziția tangentei însăși, iar unghiul de înclinare al secantei α va începe să tinde spre unghiul de înclinare al tangentei însăși α x.

Definiția 6

Tangenta la graficul funcției y = f (x) în punctul A este considerată a fi poziția limită a secantei A B, deoarece B tinde spre A, adică B → A.

Acum să trecem la considerarea semnificației geometrice a derivatei unei funcții într-un punct.

Să trecem la considerarea secantei A B pentru funcția f (x), unde A și B cu coordonatele x 0, f (x 0) și x 0 + ∆ x, f (x 0 + ∆ x) și ∆ x este notat ca increment al argumentului . Acum funcția va lua forma ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . Pentru claritate, să dăm un exemplu de desen.

Se consideră triunghiul dreptunghic rezultat A B C. Folosim definiția tangentei pentru a rezolva, adică obținem relația ∆ y ∆ x = t g α . Din definiția unei tangente rezultă că lim ∆ x → 0 ∆ y ∆ x = t g α x . Conform regulii derivatei într-un punct, avem că derivata f (x) în punctul x 0 se numește limita raportului dintre incrementul funcției și incrementul argumentului, unde ∆ x → 0 , atunci o notăm f (x 0) = lim ∆ x → 0 ∆ y ∆ x .

Rezultă că f " (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, unde k x este notat ca panta tangentei.

Adică, constatăm că f' (x) poate exista în punctul x 0, și ca tangente la un grafic dat al funcției în punctul de tangență egal cu x 0, f 0 (x 0), unde valoarea lui panta tangentei în punctul este egală cu derivata în punctul x 0 . Atunci obținem că k x = f " (x 0) .

Sensul geometric derivată a unei funcții într-un punct este că este dat conceptul existenței unei tangente la graficul în același punct.

Pentru a scrie ecuația oricărei drepte pe un plan, este necesar să existe un coeficient unghiular cu punctul prin care trece. Notația sa este considerată x 0 la intersecție.

Ecuația tangentă la graficul funcției y = f (x) în punctul x 0, f 0 (x 0) ia forma y = f "(x 0) x - x 0 + f (x 0).

Aceasta înseamnă că valoarea finală a derivatei f „(x 0) poate determina poziția tangentei, adică pe verticală, cu condiția lim x → x 0 + 0 f „(x) = ∞ și lim x → x 0 - 0 f "(x ) = ∞ sau absență deloc în condiția lim x → x 0 + 0 f " (x) ≠ lim x → x 0 - 0 f " (x) .

Locația tangentei depinde de valoarea coeficientului ei unghiular k x = f "(x 0). Când este paralelă cu axa o x, obținem că k k = 0, când paralel cu o y - k x = ∞ și forma ecuația tangentă x = x 0 crește cu k x > 0, scade pe măsură ce k x< 0 .

Exemplul 2

Alcătuiți o ecuație pentru tangenta la graficul funcției y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 în punctul cu coordonatele (1; 3) și determinați unghiul de înclinare.

Soluţie

Prin condiție avem ca funcția să fie definită pentru toți numere reale. Constatăm că punctul cu coordonatele specificate de condiția, (1; 3) este un punct de tangență, atunci x 0 = - 1, f (x 0) = - 3.

Este necesar să găsiți derivata în punctul cu valoarea - 1. Înțelegem asta

y " = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = e x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = e x + 1 + x 2 - 6 - 3 3 y " (x 0) = y " (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3

Valoarea lui f' (x) în punctul de tangență este panta tangentei, care este egală cu tangentei pantei.

Atunci k x = t g α x = y " (x 0) = 3 3

Rezultă că α x = a r c t g 3 3 = π 6

Răspuns: ecuația tangentei ia forma

y = f " (x 0) x - x 0 + f (x 0) y = 3 3 (x + 1) - 3 y = 3 3 x - 9 - 3 3

Pentru claritate, dăm un exemplu într-o ilustrație grafică.

Culoarea neagră este folosită pentru graficul funcției originale, Culoarea albastră– imaginea unei tangente, punct roșu – punct de tangență. Figura din dreapta arată o vedere mărită.

Exemplul 3

Determinați existența unei tangente la graficul unei funcții date
y = 3 · x - 1 5 + 1 în punctul cu coordonatele (1 ; 1) . Scrieți o ecuație și determinați unghiul de înclinare.

Soluţie

Prin condiție, avem că domeniul de definire al unei funcții date este considerat a fi mulțimea tuturor numerelor reale.

Să trecem la găsirea derivatei

y " = 3 x - 1 5 + 1 " = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5

Dacă x 0 = 1, atunci f' (x) este nedefinit, dar limitele sunt scrise ca lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 · 1 + 0 = + ∞ și lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , ceea ce înseamnă existența tangentă verticală în punctul (1; 1).

Răspuns: ecuația va lua forma x = 1, unde unghiul de înclinare va fi egal cu π 2.

Pentru claritate, să-l descriem grafic.

Exemplul 4

Aflați punctele de pe graficul funcției y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2, unde

1. Nu există tangentă;
2. Tangenta este paralelă cu x;
3. Tangenta este paralelă cu dreapta y = 8 5 x + 4.

Soluţie

Este necesar să se acorde atenție domeniului de aplicare al definiției. Prin condiție, avem că funcția este definită pe mulțimea tuturor numerelor reale. Extindem modulul și rezolvăm sistemul cu intervale x ∈ - ∞ ; 2 şi [-2; + ∞). Înțelegem asta

y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; + ∞)

Este necesar să se diferențieze funcția. Avem asta

y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 ", x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; + ∞)

Când x = − 2, atunci derivata nu există deoarece limitele unilaterale nu sunt egale în acel punct:

lim x → - 2 - 0 y " (x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y " (x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

Calculăm valoarea funcției în punctul x = - 2, de unde obținem asta

1. y (- 2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2, adică tangenta în punctul ( - 2; - 2) nu va exista.
2. Tangenta este paralelă cu x când panta este zero. Atunci k x = t g α x = f "(x 0). Adică, este necesar să se găsească valorile unui astfel de x atunci când derivata funcției o transformă la zero. Adică, valorile lui f ' (x) vor fi punctele de tangență, unde tangenta este paralelă cu x .

Când x ∈ - ∞ ; - 2, atunci - 1 5 (x 2 + 12 x + 35) = 0, iar pentru x ∈ (- 2; + ∞) obținem 1 5 (x 2 - 4 x + 3) = 0.

1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞

Calculați valorile funcției corespunzătoare

y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3

Prin urmare - 5; 8 5, - 4; 4 3, 1; 8 5, 3; 4 3 sunt considerate a fi punctele necesare ale graficului funcției.

Să ne uităm la o reprezentare grafică a soluției.

Linia neagră este graficul funcției, punctele roșii sunt punctele de tangență.

1. Când liniile sunt paralele, coeficienții unghiulari sunt egali. Apoi este necesar să căutați puncte pe graficul funcției unde panta va fi egală cu valoarea 8 5. Pentru a face acest lucru, trebuie să rezolvați o ecuație de forma y "(x) = 8 5. Atunci, dacă x ∈ - ∞; - 2, obținem că - 1 5 (x 2 + 12 x + 35) = 8 5, iar dacă x ∈ ( - 2 ; + ∞), atunci 1 5 (x 2 - 4 x + 3) = 8 5.

Prima ecuație nu are rădăcini deoarece discriminantul este mai mic decât zero. Să scriem asta

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0

O altă ecuație are două rădăcini reale, deci

1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞

Să trecem la găsirea valorilor funcției. Înțelegem asta

y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3

Puncte cu valori - 1; 4 15, 5; 8 3 sunt punctele în care tangentele sunt paralele cu dreapta y = 8 5 x + 4.

Răspuns: linie neagră – graficul funcției, linie roșie – graficul lui y = 8 5 x + 4, linie albastră – tangente în puncte - 1; 4 15, 5; 8 3.

Poate exista un număr infinit de tangente pentru funcții date.

Exemplul 5

Scrieți ecuațiile tuturor tangentelor disponibile ale funcției y = 3 cos 3 2 x - π 4 - 1 3, care sunt situate perpendicular pe dreapta y = - 2 x + 1 2.

Soluţie

Pentru a compila ecuația tangentei, este necesar să se găsească coeficientul și coordonatele punctului tangente, pe baza condiției de perpendicularitate a dreptelor. Definiția este următoarea: produsul coeficienților unghiulari care sunt perpendiculari pe liniile drepte este egal cu - 1, adică scris ca k x · k ⊥ = - 1. Din condiția avem că coeficientul unghiular este situat perpendicular pe dreapta și este egal cu k ⊥ = - 2, atunci k x = - 1 k ⊥ = - 1 - 2 = 1 2.

Acum trebuie să găsiți coordonatele punctelor de atingere. Trebuie să găsiți x și apoi valoarea lui pentru o funcție dată. Rețineți că din sensul geometric al derivatei la punct
x 0 obținem că k x = y "(x 0). Din această egalitate găsim valorile lui x pentru punctele de contact.

Înțelegem asta

y " (x 0) = 3 cos 3 2 x 0 - π 4 - 1 3 " = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 = - 9 2 sin 3 2 x 0 - π 4 ⇒ k x = y " (x 0) ⇔ - 9 2 sin 3 2 x 0 - π 4 = 1 2 ⇒ sin 3 2 x 0 - π 4 = - 1 9

Această ecuație trigonometrică va fi folosită pentru a calcula ordonatele punctelor tangente.

3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk sau 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk

3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk sau 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk sau x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z este o mulțime de numere întregi.

au fost găsite x puncte de contact. Acum trebuie să treceți la căutarea valorilor lui y:

y 0 = 3 cos 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - sin 2 3 2 x 0 - π 4 - 1 3 sau y 0 = 3 - 1 - sin 2 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - - 1 9 2 - 1 3 sau y 0 = 3 - 1 - - 1 9 2 - 1 3

y 0 = 4 5 - 1 3 sau y 0 = - 4 5 + 1 3

Din aceasta obținem că 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; - 4 5 + 1 3 sunt punctele de tangență.

Răspuns: ecuaţiile necesare se vor scrie ca

y = 1 2 x - 2 3 π 4 - a r c sin 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + a r c sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z

Pentru o reprezentare vizuală, luați în considerare o funcție și o tangentă pe o dreaptă de coordonate.

Figura arată că funcţia este situată pe intervalul [ - 10 ; 10 ], unde linia neagră este graficul funcției, liniile albastre sunt tangente, care sunt situate perpendicular pe dreapta dată de forma y = - 2 x + 1 2. Punctele roșii sunt puncte de atingere.

Ecuațiile canonice ale curbelor de ordinul 2 nu sunt funcții cu o singură valoare. Ecuațiile tangente pentru ele sunt compilate conform schemelor cunoscute.

Tangent la un cerc

A defini un cerc cu centru în punctul x c e n t e r ; y c e n t e r şi raza R, aplicaţi formula x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 .

Această egalitate poate fi scrisă ca o unire a două funcții:

y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r

Prima funcție este situată în partea de sus, iar a doua în partea de jos, așa cum se arată în figură.

Pentru a compila ecuația unui cerc în punctul x 0; y 0 , care este situat în semicercul superior sau inferior, ar trebui să găsiți ecuația graficului unei funcții de forma y = R 2 - x - x c e n t e r 2 + y c e n t e r sau y = - R 2 - x - x c e n t e r 2 + y c e n t e r la punctul indicat.

Când în punctele x c ​​e n t e r ; y c e n t e r + R și x ce n t e r ; y c e n t e r - R tangente pot fi date de ecuațiile y = y c e n t e r + R și y = y c e n t e r - R , iar în punctele x c ​​e n t e r + R ; y c e n t e r şi
x c e n t e r - R ; y c e n t e r va fi paralel cu o y, atunci obținem ecuații de forma x = x c e n t e r + R și x = x c e n t e r - R .

Tangent la o elipsă

Când elipsa are un centru în x c e n t e r ; y c e n t e r cu semiaxele a și b, atunci poate fi specificat folosind ecuația x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1.

O elipsă și un cerc pot fi notate prin combinarea a două funcții, și anume semielipsa superioară și inferioară. Atunci obținem asta

y = b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r

Dacă tangentele sunt situate la vârfurile elipsei, atunci ele sunt paralele cu x sau despre y. Mai jos, pentru claritate, luați în considerare figura.

Exemplul 6

Scrieți ecuația tangentei la elipsa x - 3 2 4 + y - 5 2 25 = 1 în punctele cu valorile lui x egale cu x = 2.

Soluţie

Este necesar să găsiți punctele tangente care corespund valorii x = 2. Substituim în ecuația existentă a elipsei și aflăm că

x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5

Apoi 2; 5 3 2 + 5 și 2; - 5 3 2 + 5 sunt punctele tangente care aparțin semielipsei superioare și inferioare.

Să trecem la găsirea și rezolvarea ecuației elipsei în raport cu y. Înțelegem asta

x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2

Evident, semielipsa superioară este specificată folosind o funcție de forma y = 5 + 5 2 4 - x - 3 2, iar jumătatea inferioară y = 5 - 5 2 4 - x - 3 2.

Să aplicăm un algoritm standard pentru a crea o ecuație pentru o tangentă la graficul unei funcții într-un punct. Să scriem că ecuația pentru prima tangentă la punctul 2; 5 3 2 + 5 vor arăta ca

y " = 5 + 5 2 4 - x - 3 2 " = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y " (x 0) = y " (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5

Constatăm că ecuația celei de-a doua tangente cu o valoare în punct
2; - 5 3 2 + 5 ia forma

y " = 5 - 5 2 4 - (x - 3) 2 " = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y " (x 0) = y " (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5

Grafic, tangentele sunt desemnate după cum urmează:

Tangenta la hiperbola

Când o hiperbolă are un centru în x c e n t e r ; y c e n t e r şi vârfuri x c e n t e r + α ; y c e n t e r şi x c e n t e r - α ; y c e n t e r , are loc inegalitatea x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1, dacă cu vârfuri x c e n t e r ; y c e n t e r + b și x c e n t e r ; y c e n t e r - b , atunci este specificat folosind inegalitatea x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

O hiperbolă poate fi reprezentată ca două funcții combinate ale formei

y = b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r sau y = b a · (x - x c e n t e r) 2 + a 2 + y c e n t e · r y = - b a · (x - x c e n t e r) 2 + a 2 + y c e n t e r

În primul caz avem că tangentele sunt paralele cu y, iar în al doilea sunt paralele cu x.

Rezultă că pentru a găsi ecuația tangentei la o hiperbolă este necesar să aflăm cărei funcție îi aparține punctul de tangență. Pentru a determina acest lucru, este necesar să se substituie în ecuații și să se verifice identitatea.

Exemplul 7

Scrieți o ecuație pentru tangentei la hiperbola x - 3 2 4 - y + 3 2 9 = 1 la punctul 7; - 3 3 - 3 .

Soluţie

Este necesar să se transforme înregistrarea soluției pentru găsirea unei hiperbole folosind 2 funcții. Înțelegem asta

x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 și y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3

Este necesar să se identifice cărei funcție îi aparține un punct dat cu coordonatele 7; - 3 3 - 3 .

Evident, pentru a verifica prima funcție este necesar y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3, atunci punctul nu aparține graficului, întrucât egalitatea nu se menține.

Pentru a doua funcție avem că y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3, ceea ce înseamnă că punctul aparține graficului dat. De aici ar trebui să găsiți panta.

Înțelegem asta

y " = - 3 2 (x - 3) 2 - 4 - 3 " = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y " (x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3

Răspuns: ecuaţia tangentei poate fi reprezentată ca

y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3

Este clar descris astfel:

Tangent la o parabolă

Pentru a crea o ecuație pentru tangenta la parabola y = a x 2 + b x + c în punctul x 0, y (x 0), trebuie să utilizați un algoritm standard, apoi ecuația va lua forma y = y "(x 0) x - x 0 + y ( x 0). O astfel de tangentă la vârf este paralelă cu x.

Ar trebui să definiți parabola x = a y 2 + b y + c ca uniunea a două funcții. Prin urmare, trebuie să rezolvăm ecuația pentru y. Înțelegem asta

x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a

Înfățișat grafic ca:

Pentru a afla dacă un punct x 0, y (x 0) aparține unei funcții, procedați ușor conform algoritmului standard. O astfel de tangentă va fi paralelă cu o y față de parabolă.

Exemplul 8

Scrieți ecuația tangentei la graficul x - 2 y 2 - 5 y + 3 când avem un unghi de tangentă de 150 °.

Soluţie

Începem soluția reprezentând parabola ca două funcții. Înțelegem asta

2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4

Valoarea pantei este egală cu valoarea derivatei în punctul x 0 al acestei funcții și este egală cu tangentei unghiului de înclinare.

Primim:

k x = y „(x 0) = t g α x = t g 150 ° = - 1 3

De aici determinăm valoarea x pentru punctele de contact.

Prima funcție va fi scrisă ca

y " = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3

Evident, nu există rădăcini reale, deoarece am primit o valoare negativă. Concluzionăm că nu există o tangentă cu un unghi de 150° pentru o astfel de funcție.

A doua funcție va fi scrisă ca

y " = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4

Avem că punctele de contact sunt 23 4 ; - 5 + 3 4 .

Răspuns: ecuația tangentei ia forma

y = - 1 3 x - 23 4 + - 5 + 3 4

Să o reprezentăm grafic astfel:

Dacă observați o eroare în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter

Y = f(x) și dacă în acest punct se poate desena o tangentă la graficul funcției care nu este perpendiculară pe axa absciselor, atunci coeficientul unghiular al tangentei este egal cu f"(a). Avem deja folosit aceasta de mai multe ori. De exemplu, în § 33 s-a stabilit că graficul funcției y = sin x (sinusoid) la origine formează un unghi de 45° cu axa x (mai precis, tangenta la graficul de la origine formează un unghi de 45° cu direcția pozitivă a axei x), iar în exemplul 5 § 33 de puncte au fost găsite în programul dat funcții, în care tangenta este paralelă cu axa x. În exemplul 2 din § 33, s-a întocmit o ecuație pentru tangenta la graficul funcției y = x 2 în punctul x = 1 (mai precis, la punctul (1; 1), dar mai des doar valoarea abscisei este indicat, crezând că dacă se cunoaște valoarea abscisei, atunci valoarea ordonatei poate fi găsită din ecuația y = f(x)). În această secțiune vom dezvolta un algoritm pentru alcătuirea unei ecuații tangente la graficul oricărei funcții.

Să fie date funcția y = f(x) și punctul M (a; f(a)) și se știe, de asemenea, că f"(a) există. Să creăm o ecuație pentru tangenta la graficul funcţie dată în punct dat. Această ecuație, ca și ecuația oricărei drepte care nu este paralelă cu axa ordonatelor, are forma y = kx+m, deci sarcina este de a găsi valorile coeficienților k și m.

Nu există probleme cu coeficientul unghiular k: știm că k = f "(a). Pentru a calcula valoarea lui m, folosim faptul că dreapta dorită trece prin punctul M(a; f (a)) Aceasta înseamnă că dacă înlocuim punctul de coordonate M în ecuația dreptei, obținem egalitatea corectă: f(a) = ka+m, din care aflăm că m = f(a) - ka.
Rămâne să înlocuiți valorile găsite ale coeficienților kit-ului în ecuația Drept:

Am obținut ecuația tangentei la graficul funcției y = f(x) în punctul x=a.
Dacă, să zicem,
Înlocuind valorile găsite a = 1, f(a) = 1 f"(a) = 2 în ecuația (1), obținem: y = 1+2(x-f), adică y = 2x-1.
Comparați acest rezultat cu cel obținut în exemplul 2 din § 33. Desigur, același lucru s-a întâmplat.
Să creăm o ecuație pentru tangenta la graficul funcției y = tan x la origine. Avem: aceasta înseamnă cos x f"(0) = 1. Înlocuind valorile găsite a = 0, f(a) = 0, f"(a) = 1 în ecuația (1), obținem: y = x.
De aceea am trasat tangentoidul în § 15 (vezi Fig. 62) prin originea coordonatelor la un unghi de 45° față de axa absciselor.
Rezolvându-le suficient exemple simple, am folosit de fapt un anumit algoritm, care este conținut în formula (1). Să explicăm acest algoritm.

ALGORITM DE DEZVOLTARE A ECUATIEI PENTRU O TANGENTA LA GRAFICUL FUNCTIEI y = f(x)

1) Desemnați abscisa punctului tangent cu litera a.
2) Calculați 1 (a).
3) Aflați f"(x) și calculați f"(a).
4) Înlocuiți numerele găsite a, f(a), (a) în formula (1).

Exemplul 1. Scrieți o ecuație pentru tangenta la graficul funcției în punctul x = 1.
Să folosim algoritmul, ținând cont de faptul că în acest exemplu

În fig. 126 este reprezentată o hiperbolă, se construiește o linie dreaptă y = 2.
Desenul confirmă calculele de mai sus: într-adevăr, linia y = 2 atinge hiperbola în punctul (1; 1).

Răspuns: y = 2- x.
Exemplul 2. Desenați o tangentă la graficul funcției astfel încât să fie paralelă cu dreapta y = 4x - 5.
Să clarificăm formularea problemei. Cerința de a „trage o tangentă” înseamnă de obicei „a forma o ecuație pentru tangentă”. Acest lucru este logic, deoarece dacă o persoană a fost capabilă să creeze o ecuație pentru o tangentă, atunci este puțin probabil să aibă dificultăți în construirea unei linii drepte pe planul de coordonate folosind ecuația acesteia.
Să folosim algoritmul pentru alcătuirea ecuației tangentei, ținând cont de faptul că în acest exemplu Dar, spre deosebire de exemplul anterior, există o ambiguitate: abscisa punctului tangentei nu este indicată în mod explicit.
Să începem să gândim așa. Tangenta dorită trebuie să fie paralelă cu dreapta y = 4x-5. Două drepte sunt paralele dacă și numai dacă panta lor este egală. Aceasta înseamnă că coeficientul unghiular al tangentei trebuie să fie egal cu coeficientul unghiular al dreptei date: Astfel, putem găsi valoarea lui a din ecuația f"(a) = 4.
Avem:
Din ecuație Aceasta înseamnă că există două tangente care îndeplinesc condițiile problemei: una în punctul cu abscisa 2, cealaltă în punctul cu abscisa -2.
Acum puteți urma algoritmul.

Exemplul 3. Din punctul (0; 1) trageți o tangentă la graficul funcției
Să folosim algoritmul pentru alcătuirea ecuației tangentei, ținând cont că în acest exemplu, Rețineți că aici, ca și în exemplul 2, abscisa punctului tangentei nu este indicată în mod explicit. Cu toate acestea, urmăm algoritmul.

Prin condiție, tangenta trece prin punctul (0; 1). Înlocuind valorile x = 0, y = 1 în ecuația (2), obținem:
După cum puteți vedea, în acest exemplu, abia la pasul al patrulea al algoritmului am reușit să găsim abscisa punctului tangent. Înlocuind valoarea a =4 în ecuația (2), obținem:

În fig. 127 prezintă o ilustrare geometrică a exemplului considerat: este trasat un grafic al funcției

În § 32 am observat că pentru o funcție y = f(x) având o derivată la un punct fix x, egalitatea aproximativă este valabilă:

Pentru comoditatea unui raționament suplimentar, să schimbăm notația: în loc de x vom scrie a, în loc de x, și, în consecință, în loc de x-a. Atunci egalitatea aproximativă scrisă mai sus va lua forma:

Acum uitați-vă la fig. 128. Se trasează o tangentă la graficul funcției y = f(x) în punctul M (a; f (a)). Punctul x este marcat pe axa x aproape de a. Este clar că f(x) este ordonata graficului funcției în punctul x specificat. Ce este f(a) + f"(a) (x-a)? Aceasta este ordonata tangentei corespunzătoare aceluiași punct x - vezi formula (1). Care este sensul egalității aproximative (3)? Faptul că Pentru a calcula valoarea aproximativă a funcției, luați valoarea ordonată a tangentei.

Exemplul 4. Găsiți valoarea aproximativă expresie numerică 1,02 7 .
Este despre despre găsirea valorii funcției y = x 7 în punctul x = 1,02. Să folosim formula (3), ținând cont de faptul că în acest exemplu
Ca rezultat obținem:

Dacă folosim un calculator, obținem: 1,02 7 = 1,148685667...
După cum puteți vedea, acuratețea aproximării este destul de acceptabilă.
Răspuns: 1,02 7 =1,14.

A.G. Mordkovich Algebra clasa a X-a

Calendar-planificare tematică în matematică, videoîn matematică online, descărcare Matematică la școală

Conținutul lecției notele de lecție sprijinirea metodelor de accelerare a prezentării lecției cadru tehnologii interactive Practică sarcini și exerciții ateliere de autotestare, instruiri, cazuri, întrebări teme pentru acasă întrebări de discuție întrebări retorice de la elevi Ilustrații audio, clipuri video și multimedia fotografii, imagini, grafice, tabele, diagrame, umor, anecdote, glume, benzi desenate, pilde, proverbe, cuvinte încrucișate, citate Suplimente rezumate articole trucuri pentru pătuțurile curioși manuale dicționar de bază și suplimentar de termeni altele Îmbunătățirea manualelor și lecțiilorcorectarea erorilor din manual actualizarea unui fragment dintr-un manual, elemente de inovație în lecție, înlocuirea cunoștințelor învechite cu altele noi Doar pentru profesori lecții perfecte plan calendaristic pentru un an instrucțiuni programe de discuții Lecții integrate

Ecuația tangentei la graficul unei funcții

P. Romanov, T. Romanova,
Magnitogorsk,
Regiunea Chelyabinsk

Ecuația tangentei la graficul unei funcții

Articolul a fost publicat cu sprijinul Complexului Hotelier ITAKA+. Când stați în orașul constructorilor de nave Severodvinsk, nu veți întâmpina problema găsirii unei locuințe temporare. , pe site-ul complexului hotelier „ITHAKA+” http://itakaplus.ru, puteți închiria ușor și rapid un apartament în oraș, pentru orice perioadă, cu o plată zilnică.

Pe scena modernă dezvoltarea educației, una dintre sarcinile sale principale este formarea unei personalități care gândesc creativ. Capacitatea de creativitate la studenți poate fi dezvoltată numai dacă aceștia sunt implicați sistematic în bazele activităților de cercetare. Fundația pentru ca elevii să-și folosească puterile, abilitățile și talentele creative este formată de cunoștințe și abilități cu drepturi depline. În acest sens, problema formării unui sistem de cunoștințe și abilități de bază pentru fiecare subiect al cursului de matematică școlară este de o importanță nu mică. În același timp, abilitățile cu drepturi depline ar trebui să fie scopul didactic nu al sarcinilor individuale, ci al unui sistem atent gândit al acestora. În sensul cel mai larg, un sistem este înțeles ca un set de elemente interconectate care interacționează care au integritate și o structură stabilă.

Să luăm în considerare o tehnică pentru a-i învăța pe elevi cum să scrie o ecuație pentru o tangentă la graficul unei funcții. În esență, toate problemele de găsire a ecuației tangentei se rezumă la necesitatea de a selecta dintr-o mulțime (mănunchi, familie) de linii pe acelea care satisfac o anumită cerință - sunt tangente la graficul unei anumite funcții. În acest caz, setul de linii din care se efectuează selecția poate fi specificat în două moduri:

a) un punct situat pe planul xOy (creion central de linii);
b) coeficient unghiular (fascicul paralel de drepte).

În acest sens, la studierea subiectului „Tangentă la graficul unei funcții” pentru a izola elementele sistemului, am identificat două tipuri de probleme:

1) probleme pe o tangentă dată de punctul prin care trece;
2) probleme pe o tangentă dată de panta acesteia.

Instruirea în rezolvarea problemelor tangente a fost realizată folosind algoritmul propus de A.G. Mordkovici. A lui diferenta fundamentala dintre cele deja cunoscute este că abscisa punctului de tangență se notează cu litera a (în loc de x0), și de aceea ecuația tangentei ia forma

y = f(a) + f "(a)(x – a)

(comparați cu y = f(x 0) + f „(x 0)(x – x 0)). Această tehnică metodologică, în opinia noastră, permite elevilor să înțeleagă rapid și ușor unde sunt scrise coordonatele punctului curent în ecuația tangentei generale și unde sunt punctele de contact.

Algoritm pentru alcătuirea ecuației tangente la graficul funcției y = f(x)

1. Desemnați abscisa punctului tangent cu litera a.
2. Găsiți f(a).
3. Găsiți f „(x) și f „(a).
4. Înlocuiți numerele găsite a, f(a), f "(a) în ecuația generală tangentă y = f(a) = f "(a)(x – a).

Acest algoritm poate fi compilat pe baza identificării independente a operațiunilor de către studenți și a secvenței implementării lor.

Practica a arătat că soluția secvențială a fiecăreia dintre problemele cheie folosind un algoritm vă permite să dezvoltați abilitățile de a scrie ecuația unei tangente la graficul unei funcții în etape, iar pașii algoritmului servesc drept puncte de referință pentru acțiuni. . Această abordare corespunde teoriei formării treptate a acțiunilor mentale dezvoltată de P.Ya. Galperin și N.F. Talizina.

În primul tip de sarcini au fost identificate două sarcini cheie:

• tangenta trece printr-un punct situat pe curbă (problema 1);
• tangenta trece printr-un punct care nu se află pe curbă (problema 2).

Sarcina 1. Scrieți o ecuație pentru tangenta la graficul funcției în punctul M(3; – 2).

Soluţie. Punctul M(3; – 2) este un punct tangent, deoarece

1. a = 3 – abscisa punctului tangent.
2. f(3) = – 2.
3. f „(x) = x 2 – 4, f „(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – ecuația tangentei.

Problema 2. Scrieți ecuațiile tuturor tangentelor la graficul funcției y = – x 2 – 4x + 2 care trece prin punctul M(– 3; 6).

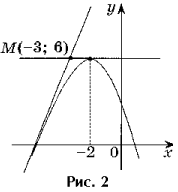Soluţie. Punctul M(– 3; 6) nu este un punct tangent, deoarece f(– 3) 6 (Fig. 2).

2. f(a) = – a 2 – 4a + 2.
3. f „(x) = – 2x – 4, f „(a) = – 2a – 4.
4. y = – a 2 – 4a + 2 – 2(a + 2)(x – a) – ecuația tangentei.

Tangenta trece prin punctul M(– 3; 6), prin urmare, coordonatele ei satisfac ecuația tangentei.

6 = – a 2 – 4a + 2 – 2(a + 2)(– 3 – a),
a 2 + 6a + 8 = 0^ a 1 = – 4, a 2 = – 2.

Dacă a = – 4, atunci ecuația tangentei este y = 4x + 18.

Dacă a = – 2, atunci ecuația tangentei are forma y = 6.

În al doilea tip, sarcinile cheie vor fi următoarele:

• tangenta este paralelă cu o dreaptă (problema 3);
• tangenta trece la un anumit unghi fata de dreapta data (problema 4).

Problema 3. Scrieți ecuațiile tuturor tangentelor la graficul funcției y = x 3 – 3x 2 + 3, paralele cu dreapta y = 9x + 1.

Soluţie.

1. a – abscisa punctului tangent.
2. f(a) = a 3 – 3a 2 + 3.
3. f „(x) = 3x 2 – 6x, f „(a) = 3a 2 – 6a.

Dar, pe de altă parte, f "(a) = 9 (condiția de paralelism). Aceasta înseamnă că trebuie să rezolvăm ecuația 3a 2 – 6a = 9. Rădăcinile sale sunt a = – 1, a = 3 (Fig. 3). ).

4. 1) a = – 1;
2) f(– 1) = – 1;
3) f "(– 1) = 9;
4) y = – 1 + 9(x + 1);

y = 9x + 8 – ecuația tangentei;

1) a = 3;
2) f(3) = 3;
3) f „(3) = 9;
4) y = 3 + 9(x – 3);

y = 9x – 24 – ecuația tangentei.

Problema 4. Scrieți ecuația tangentei la graficul funcției y = 0,5x 2 – 3x + 1, trecând cu un unghi de 45° la dreapta y = 0 (Fig. 4).

Soluţie. Din condiția f „(a) = tan 45° găsim a: a – 3 = 1^a = 4.

1. a = 4 – abscisa punctului tangent.
2. f(4) = 8 – 12 + 1 = – 3.
3. f „(4) = 4 – 3 = 1.
4. y = – 3 + 1(x – 4).

y = x – 7 – ecuația tangentei.

Este ușor să arăți că soluția oricărei alte probleme se rezumă la rezolvarea uneia sau mai multor probleme cheie. Luați în considerare următoarele două probleme ca exemplu.

1. Scrieți ecuațiile tangentelor la parabola y = 2x 2 – 5x – 2, dacă tangentele se intersectează în unghi drept și una dintre ele atinge parabola în punctul cu abscisa 3 (Fig. 5).

Soluţie. Deoarece abscisa punctului tangent este dată, prima parte a soluției este redusă la problema cheie 1.

1. a = 3 – abscisa punctului de tangenta a uneia dintre laturile unghiului drept.
2. f(3) = 1.
3. f „(x) = 4x – 5, f „(3) = 7.
4. y = 1 + 7(x – 3), y = 7x – 20 – ecuația primei tangente.

Lasă a – unghiul de înclinare al primei tangente. Deoarece tangentele sunt perpendiculare, atunci este unghiul de înclinare al celei de-a doua tangente. Din ecuația y = 7x – 20 a primei tangente avem tg a = 7. Să găsim

Aceasta înseamnă că panta celei de-a doua tangente este egală cu .

Soluția ulterioară se reduce la sarcina cheie 3.

Fie B(c; f(c)) punctul de tangență al celei de-a doua drepte, atunci

1. – abscisa celui de-al doilea punct de tangenta.
2.
3.
4.
– ecuația celei de-a doua tangente.

Notă. Coeficientul unghiular al tangentei poate fi găsit mai ușor dacă elevii cunosc raportul dintre coeficienții dreptelor perpendiculare k 1 k 2 = – 1.

2. Scrieți ecuațiile tuturor tangentelor comune la graficele funcțiilor

Soluţie. Sarcina se rezumă la găsirea abscisei punctelor tangente ale tangentelor comune, adică rezolvarea problemei cheie 1 în formă generală, elaborarea unui sistem de ecuații și apoi rezolvarea acestuia (Fig. 6).

1. Fie a abscisa punctului tangent situat pe graficul funcției y = x 2 + x + 1.
2. f(a) = a 2 + a + 1.
3. f „(a) = 2a + 1.
4. y = a 2 + a + 1 + (2a + 1)(x – a) = (2a + 1)x + 1 – a 2 .

1. Fie c abscisa punctului tangent situat pe graficul funcției
2.
3. f „(c) = c.
4.

Din moment ce tangentele sunt generale, atunci

Deci y = x + 1 și y = – 3x – 3 sunt tangente comune.

Scopul principal al sarcinilor luate în considerare este de a pregăti elevii să recunoască în mod independent tipul de problemă cheie atunci când rezolvă probleme mai complexe care necesită anumite abilități de cercetare (capacitatea de a analiza, compara, generaliza, prezenta o ipoteză etc.). Astfel de sarcini includ orice sarcină în care sarcina cheie este inclusă ca componentă. Să luăm ca exemplu problema (inversa cu problema 1) de a găsi o funcție din familia tangentelor sale.

3. Pentru ce b și c sunt dreptele y = x și y = – 2x tangente la graficul funcției y = x 2 + bx + c?

Soluţie.

Fie t abscisa punctului de tangență al dreptei y = x cu parabola y = x 2 + bx + c; p este abscisa punctului de tangență al dreptei y = – 2x cu parabola y = x 2 + bx + c. Atunci ecuația tangentei y = x va lua forma y = (2t + b)x + c – t 2 , iar ecuația tangentei y = – 2x va lua forma y = (2p + b)x + c – p 2 .

Să compunem și să rezolvăm un sistem de ecuații

Răspuns:

Probleme de rezolvat independent

1. Scrieți ecuațiile tangentelor trasate la graficul funcției y = 2x 2 – 4x + 3 în punctele de intersecție ale graficului cu dreapta y = x + 3.

Răspuns: y = – 4x + 3, y = 6x – 9,5.

2. Pentru ce valori ale lui a trece tangenta trasată la graficul funcției y = x 2 – ax în punctul graficului cu abscisa x 0 = 1 prin punctul M(2; 3)?

Răspuns: a = 0,5.

3. Pentru ce valori ale lui p linia dreaptă y = px – 5 atinge curba y = 3x 2 – 4x – 2?

Răspuns: p 1 = – 10, p 2 = 2.

4. Aflați toate punctele comune ale graficului funcției y = 3x – x 3 și tangenta trasată la acest grafic prin punctul P(0; 16).

Răspuns: A(2; – 2), B(– 4; 52).

5. Aflați cea mai scurtă distanță dintre parabola y = x 2 + 6x + 10 și linia dreaptă

Răspuns:

6. Pe curba y = x 2 – x + 1, găsiți punctul în care tangenta la grafic este paralelă cu dreapta y – 3x + 1 = 0.

Răspuns: M(2; 3).

7. Scrieți ecuația tangentei la graficul funcției y = x 2 + 2x – | 4x |, care îl atinge în două puncte. Faceți un desen.

Răspuns: y = 2x – 4.

8. Demonstrați că dreapta y = 2x – 1 nu intersectează curba y = x 4 + 3x 2 + 2x. Găsiți distanța dintre punctele lor cele mai apropiate.

Răspuns:

9. Pe parabola y = x 2 se iau două puncte cu abscisele x 1 = 1, x 2 = 3. Prin aceste puncte se trasează o secantă. În ce punct al parabolei tangenta la aceasta va fi paralelă cu secantei? Scrieți ecuațiile secante și tangente.

Răspuns: y = 4x – 3 – ecuație secante; y = 4x – 4 – ecuația tangentei.

10. Aflați unghiul q între tangentele la graficul funcției y = x 3 – 4x 2 + 3x + 1, trasate în punctele cu abscisele 0 și 1.

Răspuns: q = 45°.

11. În ce puncte tangenta la graficul funcției formează un unghi de 135° cu axa Ox?

Răspuns: A(0; – 1), B(4; 3).

12. În punctul A(1; 8) la curbă se trasează o tangentă. Aflați lungimea segmentului tangent dintre axele de coordonate.

Răspuns:

13. Scrieți ecuația tuturor tangentelor comune la graficele funcțiilor y = x 2 – x + 1 și y = 2x 2 – x + 0,5.

Răspuns: y = – 3x și y = x.

14. Aflați distanța dintre tangentele la graficul funcției paralel cu axa x.

Răspuns:

15. Determinați în ce unghiuri intersectează parabola y = x 2 + 2x – 8 axa x.

Răspuns: q 1 = arctan 6, q 2 = arctan (– 6).

16. Graficul funcției găsiți toate punctele, tangenta la fiecare dintre ele la acest grafic intersectează semiaxele pozitive ale coordonatelor, decupând segmente egale din ele.

Răspuns: A(– 3; 11).

17. Linia y = 2x + 7 și parabola y = x 2 – 1 se intersectează în punctele M și N. Aflați punctul K de intersecție al dreptelor tangente la parabolă în punctele M și N.

Răspuns: K(1; – 9).

18. Pentru ce valori ale lui b este linia y = 9x + b tangentă la graficul funcției y = x 3 – 3x + 15?

Raspunsul 1; 31.

19. Pentru ce valori ale lui k linia dreaptă y = kx – 10 are doar una punct comun cu graficul funcției y = 2x 2 + 3x – 2? Pentru valorile găsite ale lui k, determinați coordonatele punctului.

Răspuns: k 1 = – 5, A(– 2; 0); k2 = 11, B(2; 12).

20. Pentru ce valori ale lui b trece tangenta trasată la graficul funcției y = bx 3 – 2x 2 – 4 în punctul cu abscisa x 0 = 2 prin punctul M(1; 8)?

Răspuns: b = – 3.

21. O parabolă cu un vârf pe axa Ox atinge dreapta care trece prin punctele A(1; 2) și B(2; 4) în punctul B. Aflați ecuația parabolei.

Răspuns:

22. La ce valoare a coeficientului k atinge parabola y = x 2 + kx + 1 de axa Ox?

Răspuns: k = d 2.

23. Aflați unghiurile dintre dreapta y = x + 2 și curba y = 2x 2 + 4x – 3.

29. Aflați distanța dintre tangentele la graficul funcției și generatoarele cu direcția pozitivă a axei Ox la un unghi de 45°.

Răspuns:

30. Aflați locul vârfurilor tuturor parabolelor de forma y = x 2 + ax + b tangentă la dreapta y = 4x – 1.

Răspuns: linie dreaptă y = 4x + 3.

Literatură

1. Zvavich L.I., Shlyapochnik L.Ya., Chinkina M.V. Algebra și începuturile analizei: 3600 de probleme pentru școlari și cei care intră în universități. – M., Butarda, 1999.
2. Mordkovich A. Seminarul patru pentru profesori tineri. Subiect: Aplicații derivate. – M., „Matematică”, Nr. 21/94.
3. Formarea de cunoștințe și deprinderi pe baza teoriei asimilării treptate a acțiunilor mentale. / Ed. P.Ya. Galperina, N.F. Talizina. – M., Universitatea de Stat din Moscova, 1968.

În acest articol vom analiza toate tipurile de probleme de găsit

Să ne amintim sensul geometric al derivatului: dacă o tangentă este trasată la graficul unei funcții într-un punct, atunci coeficientul de pantă al tangentei (egal cu tangentei unghiului dintre tangentă și direcția pozitivă a axei) este egal cu derivata funcției la punct.

Să luăm un punct arbitrar pe tangenta cu coordonate:

Și luați în considerare un triunghi dreptunghic:

În acest triunghi

De aici

Aceasta este ecuația tangentei trasate la graficul funcției în punct.

Pentru a scrie ecuația tangentei, trebuie doar să cunoaștem ecuația funcției și punctul în care este trasată tangenta. Apoi putem găsi și .

Există trei tipuri principale de probleme de ecuații tangente.

1. Dat un punct de contact

2. Se dă coeficientul de pantă tangentă, adică valoarea derivatei funcției în punct.

3. Sunt date coordonatele punctului prin care se trasează tangenta, dar care nu este punctul de tangență.

Să ne uităm la fiecare tip de sarcină.

1 . Scrieți ecuația tangentei la graficul funcției la punct .

.

b) Aflați valoarea derivatei în punctul . Mai întâi să găsim derivata funcției

Să substituim valorile găsite în ecuația tangentei:

Să deschidem parantezele din partea dreaptă a ecuației. Primim:

Răspuns: .

2. Aflați abscisa punctelor în care funcțiile sunt tangente la grafic paralel cu axa x.

Dacă tangenta este paralelă cu axa x, deci unghiul dintre tangentă și direcția pozitivă a axei este zero, deci tangentea unghiului tangentei este zero. Aceasta înseamnă că valoarea derivatei funcției la punctele de contact este zero.

a) Aflați derivata funcției .

b) Să echivalăm derivata cu zero și să găsim valorile în care tangenta este paralelă cu axa:

Echivalând fiecare factor cu zero, obținem:

Răspuns: 0;3;5

3. Scrieți ecuații pentru tangente la graficul unei funcții , paralel Drept .

O tangentă este paralelă cu o dreaptă. Panta acestei drepte este -1. Deoarece tangentei este paralelă cu această dreaptă, prin urmare, panta tangentei este de asemenea -1. Acesta este cunoaștem panta tangentei, și, prin urmare, valoare derivată în punctul de tangență.

Acesta este al doilea tip de problemă pentru a găsi ecuația tangentei.

Deci, ni se dă funcția și valoarea derivatei în punctul de tangență.

a) Aflați punctele în care derivata funcției este egală cu -1.

Mai întâi, să găsim ecuația derivată.

Să echivalăm derivata cu numărul -1.

Să găsim valoarea funcției în punct.

(dupa conditie)

.

b) Aflați ecuația tangentei la graficul funcției în punctul .

Să găsim valoarea funcției în punct.

(după condiție).

Să substituim aceste valori în ecuația tangentei:

.

Răspuns:

4 . Scrieți ecuația tangentei la curbă , trecând printr-un punct

Mai întâi, să verificăm dacă punctul este un punct tangent. Dacă un punct este un punct tangent, atunci el aparține graficului funcției, iar coordonatele sale trebuie să satisfacă ecuația funcției. Să substituim coordonatele punctului în ecuația funcției.

Titlu="1sqrt(8-3^2)">. Мы получили под корнем !} un număr negativ, egalitatea nu este adevărată, iar punctul nu aparține graficului funcției și nu este un punct de contact.

Acesta este ultimul tip de problemă pentru a găsi ecuația tangentei. Primul lucru trebuie să găsim abscisa punctului tangent.

Să găsim valoarea.

Să fie punctul de contact. Punctul aparține tangentei la graficul funcției. Dacă înlocuim coordonatele acestui punct în ecuația tangentei, obținem egalitatea corectă:

.

Valoarea funcției într-un punct este .

Să găsim valoarea derivatei funcției în punct.

Mai întâi, să găsim derivata funcției. Acest .

Derivata intr-un punct este egala cu .

Să înlocuim expresiile pentru și în ecuația tangentei. Obținem ecuația pentru:

Să rezolvăm această ecuație.

Reduceți numărătorul și numitorul fracției cu 2:

Să dăm partea dreapta ecuatii la numitor comun. Primim:

Să simplificăm numărătorul fracției și să înmulțim ambele părți cu - această expresie este strict mai mare decât zero.

Obținem ecuația

Să rezolvăm. Pentru a face acest lucru, să pătram ambele părți și să trecem la sistem.

Title="delim(lbrace)(matrix(2)(1)((64-48(x_0)+9(x_0)^2=8-(x_0)^2) (8-3x_0>=0 ) ))( )">!}

Să rezolvăm prima ecuație.

Să decidem ecuație pătratică, primim

A doua rădăcină nu îndeplinește condiția title="8-3x_0>=0">, следовательно, у нас только одна точка касания и её абсцисса равна .!}

Să scriem ecuația tangentei la curbă în punct. Pentru a face acest lucru, înlocuiți valoarea în ecuație - Am înregistrat-o deja.

Răspuns:
.

O tangentă este o linie dreaptă , care atinge graficul funcției într-un punct și toate punctele care se află la cea mai mică distanță de graficul funcției. Prin urmare, tangenta trece tangentă la graficul funcției la un anumit unghi, iar mai multe tangente la unghiuri diferite nu pot trece prin punctul de tangență. Ecuațiile tangente și ecuațiile normale la graficul unei funcții sunt construite folosind derivata.

Ecuația tangentei este derivată din ecuația dreptei .

Să derivăm ecuația tangentei și apoi ecuația normalei la graficul funcției.

y = kx + b .

În el k- coeficientul unghiular.

De aici obținem următoarea intrare:

y - y 0 = k(X - X 0 ) .

Valoarea derivată f "(X 0 ) funcții y = f(X) la punct X0 egală cu panta k= tg φ tangentă la graficul unei funcții trasate printr-un punct M0 (X 0 , y 0 ) , Unde y0 = f(X 0 ) . Aceasta este sensul geometric al derivatului .

Astfel, putem înlocui k pe f "(X 0 ) și obțineți următoarele ecuația tangentei la graficul unei funcții :

y - y 0 = f "(X 0 )(X - X 0 ) .

În problemele care implică alcătuirea ecuației unei tangente la graficul unei funcții (și vom trece la ele în curând), este necesar să reducem ecuația obținută din formula de mai sus la ecuația unei drepte în formă generală. Pentru a face acest lucru, trebuie să transferați toate literele și numerele în partea stanga ecuație și lăsați zero în partea dreaptă.

Acum despre ecuația normală. Normal - aceasta este o dreaptă care trece prin punctul de tangență la graficul funcției perpendiculară pe tangentă. Ecuație normală :

(X - X 0 ) + f "(X 0 )(y - y 0 ) = 0

Pentru a vă încălzi, vi se cere să rezolvați singur primul exemplu, apoi să priviți soluția. Există toate motivele să sperăm că această sarcină nu va fi un „duș rece” pentru cititorii noștri.

Exemplul 0. Creați o ecuație tangentă și o ecuație normală pentru graficul unei funcții într-un punct M (1, 1) .

Exemplul 1. Scrieți o ecuație tangentă și o ecuație normală pentru graficul unei funcții , dacă abscisa este tangentă .

Să găsim derivata funcției:

Acum avem tot ce trebuie înlocuit în intrarea dată în ajutorul teoretic pentru a obține ecuația tangentei. Primim

În acest exemplu, am avut noroc: panta s-a dovedit a fi zero, așa că reducem separat ecuația la aspectul general nu era nevoie. Acum putem crea ecuația normală:

În figura de mai jos: graficul unei funcții culoare visiniu, tangentă Culoare verde, portocaliu normal.

Următorul exemplu nu este, de asemenea, complicat: funcția, ca și în cea precedentă, este și un polinom, dar panta nu va fi egală cu zero, așa că se va adăuga încă un pas - aducând ecuația la o formă generală.

Exemplul 2.

Soluţie. Să găsim ordonata punctului tangent:

Să găsim derivata funcției:

.

Să găsim valoarea derivatei în punctul de tangență, adică panta tangentei:

Înlocuim toate datele obținute în „formula goală” și obținem ecuația tangentei:

Aducem ecuația la forma ei generală (colectăm toate literele și numerele, altele decât zero în partea stângă și lăsăm zero în dreapta):

Compunem ecuația normală:

Exemplul 3. Scrieți ecuația tangentei și ecuația normalei la graficul funcției dacă abscisa este punctul de tangență.

Soluţie. Să găsim ordonata punctului tangent:

Să găsim derivata funcției:

.

Să găsim valoarea derivatei în punctul de tangență, adică panta tangentei:

.

Găsim ecuația tangentei:

Înainte de a aduce ecuația la forma sa generală, trebuie să o „pieptănați” puțin: înmulțiți termen cu termen cu 4. Facem acest lucru și aducem ecuația la forma sa generală:

Compunem ecuația normală:

Exemplul 4. Scrieți ecuația tangentei și ecuația normalei la graficul funcției dacă abscisa este punctul de tangență.

Soluţie. Să găsim ordonata punctului tangent:

.

Să găsim derivata funcției:

Să găsim valoarea derivatei în punctul de tangență, adică panta tangentei:

.

Obtinem ecuatia tangentei:

Aducem ecuația la forma ei generală:

Compunem ecuația normală:

O greșeală comună atunci când scrieți ecuații tangente și normale este să nu observați că funcția dată în exemplu este complexă și să calculați derivata ei ca derivată a unei funcții simple. Următoarele exemple sunt deja din funcții complexe(lecția corespunzătoare se va deschide într-o fereastră nouă).

Exemplul 5. Scrieți ecuația tangentei și ecuația normalei la graficul funcției dacă abscisa este punctul de tangență.

Soluţie. Să găsim ordonata punctului tangent:

Atenţie! Această funcție- complex, deoarece argumentul tangentei (2 X) este în sine o funcție. Prin urmare, găsim derivata unei funcții ca derivată a unei funcții complexe.