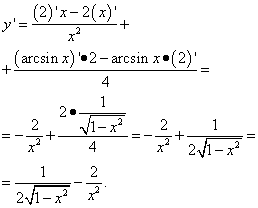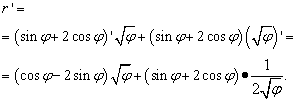Kosinuso išvestinė: (cos x)′. Trigonometrinių funkcijų dariniai: liestinė, sinusas, kosinusas ir kt

Raskite išvestinę.

1 variantas.

2 variantas.

adresu = 2X + 5.

adresu = 2X – 5.

adresu= 4 cos X.

adresu= 3 nuodėmė X.

adresu= tg X+ctg X.

adresu= tg X-ctg X.

adresu= nuodėmė 3 X.

adresu= cos 4 X.

Atsakymų variantai.

– 4 nuodėmė X

– 3 cos X

1/cos 2 X+ 1 / nuodėmė 2 X

1/cos 2 X–1/nuodėmė 2 X

1/nuodėmė 2 X–1/cos 2 X

– 4sin4 X

– 3cos3 X

f(x) = nuodėmė x+ cos x

f(x) = nuodėmė 2 x – x

f(x) = 2x+cos(4 x – )

1 variantas

2 variantas

y = 2X 3

y = 3X 2

y = 1/4 X 4 + 2X 2 – 7

y = 1/2 X 4 + 4X + 5

y = X 3 + 4X 2 – 3X.
Išspręskite lygtį y " = 0

y = 2X 3 – 9X 2 + 12X + 7.
Išspręskite lygtį y " = 0.

y= nuodėmė 2 X– cos 3 X.

y= cos 2 X– 3 nuodėmė X.

y= tg X-ctg ( X + /4).

y=ctg X+ tg( X – /4).

y= nuodėmė 2 X.

y= cos 2 X.

Atsakymų variantai.

Išvesdami pačią pirmąją lentelės formulę, vadovausimės išvestinės funkcijos apibrėžimu taške. Paimkime kur x– bet koks tikras numeris, tai yra, x– bet koks skaičius iš funkcijos apibrėžimo srities. Užrašykime funkcijos padidėjimo ir argumento prieaugio santykio ribą:

Reikėtų pažymėti, kad pagal ribinį ženklą gaunama išraiška, kuri nėra nulio neapibrėžtis, padalyta iš nulio, nes skaitiklyje yra ne be galo maža reikšmė, o tiksliai nulis. Kitaip tariant, pastovios funkcijos prieaugis visada yra lygus nuliui.

Taigi, pastovios funkcijos išvestinėyra lygus nuliui visoje apibrėžimo srityje.

Galios funkcijos išvestinė.

Galios funkcijos išvestinės formulė turi formą , kur eksponentas p– bet koks tikrasis skaičius.

Pirmiausia įrodykime natūraliojo rodiklio formulę, tai yra už p = 1, 2, 3, …

Naudosime išvestinės apibrėžimą. Užrašykime galios funkcijos padidėjimo ir argumento prieaugio santykio ribą:

Norėdami supaprastinti išraišką skaitiklyje, pereiname prie Niutono dvinario formulės:

Vadinasi,

Tai įrodo natūraliojo eksponento laipsnio funkcijos išvestinės formulę.

Eksponentinės funkcijos išvestinė.

Pateikiame išvestinės formulės išvedimą pagal apibrėžimą:

Atėjome į netikrumą. Norėdami jį išplėsti, pristatome naują kintamąjį ir . Tada . Paskutiniame perėjime naudojome perėjimo prie naujos logaritminės bazės formulę.

Pakeiskime pradinę ribą:

Jei prisiminsime antrąją reikšmingą ribą, gauname eksponentinės funkcijos išvestinės formulę:

Logaritminės funkcijos išvestinė.

Įrodykime logaritminės funkcijos išvestinės formulę visiems x iš apibrėžimo srities ir visų galiojančių bazės reikšmių a logaritmas Pagal išvestinės priemonės apibrėžimą turime:

Kaip pastebėjote, įrodinėjimo metu transformacijos buvo atliekamos naudojant logaritmo savybes. Lygybė yra tiesa dėl antrosios nepaprastos ribos.

Trigonometrinių funkcijų dariniai.

Norėdami išvesti trigonometrinių funkcijų išvestinių formules, turėsime prisiminti kai kurias trigonometrijos formules, taip pat pirmąją reikšmingą ribą.

Pagal mūsų turimos sinusinės funkcijos išvestinės apibrėžimą .

Naudokime sinusų skirtumo formulę:

Belieka pereiti prie pirmosios nepaprastos ribos:

Taigi funkcijos išvestinė nuodėmė x Yra cos x.

Lygiai taip pat įrodoma kosinuso išvestinės formulė.

Todėl funkcijos išvestinė cos x Yra – nuodėmė x.

Tangento ir kotangento išvestinių lentelės formules išvesime naudodami įrodytas diferenciacijos taisykles (trupmenos išvestinę).

Hiperbolinių funkcijų dariniai.

Diferencijavimo taisyklės ir eksponentinės funkcijos išvestinės formulė iš išvestinių lentelės leidžia išvesti hiperbolinio sinuso, kosinuso, liestinės ir kotangento išvestinių formules.

Atvirkštinės funkcijos išvestinė.

Norėdami išvengti painiavos pateikimo metu, apatiniame indekse pažymėkime funkcijos argumentą, pagal kurį atliekamas diferencijavimas, tai yra, tai yra funkcijos išvestinė f(x) Autorius x.

Dabar suformuluokime atvirkštinės funkcijos išvestinės radimo taisyklė.

Tegul funkcijos y = f(x) Ir x = g(y) tarpusavyje atvirkštiniai, apibrėžti intervalais ir atitinkamai. Jeigu taške yra baigtinė nulinė funkcijos išvestinė f(x), tada taške yra atvirkštinės funkcijos baigtinė išvestinė g(y), ir . Kitame įraše .

Šią taisyklę galima performuluoti bet kuriai x iš intervalo , tada gauname .

Patikrinkime šių formulių pagrįstumą.

Raskime atvirkštinę natūraliojo logaritmo funkciją (Čia y yra funkcija ir x- argumentas). Išsprendę šią lygtį x, gauname (čia x yra funkcija ir y– jos argumentas). Tai yra, ir tarpusavyje atvirkštines funkcijas.

Iš išvestinių lentelės matome, kad Ir .

Įsitikinkite, kad formulės, skirtos rasti atvirkštinės funkcijos išvestines, duoda tuos pačius rezultatus:

Pateikiamas kosinuso - cos(x) išvestinės formulės įrodymas ir išvedimas. Cos 2x, cos 3x, cos nx, kosinuso kvadratu, kubu ir laipsniu n išvestinių skaičiavimo pavyzdžiai. N-osios eilės kosinuso išvestinės formulė.

Išvestinė kintamojo x atžvilgiu iš x kosinuso yra lygi minus x sinusui:
(cos x)′ = - sin x.

Įrodymas

Norėdami gauti kosinuso išvestinės formulę, naudojame išvestinės apibrėžimą:
.

Transformuokime šią išraišką, kad sumažintume ją iki žinomų matematinių dėsnių ir taisyklių. Norėdami tai padaryti, turime žinoti keturias savybes.
1) Trigonometrinės formulės. Mums reikės šios formulės:
(1) ;
2) Sinuso funkcijos tęstinumo savybė:
(2) ;
3) Pirmosios ypatingos ribos reikšmė:
(3) ;
4) Dviejų funkcijų sandaugos ribos savybė:
Jei ir , tada
(4) .

Taikykime šiuos įstatymus iki galo. Pirmiausia transformuojame algebrinę išraišką
.
Norėdami tai padaryti, taikome formulę
(1) ;
Mūsų atveju
; . Tada
;
;
;
.

Padarykime pakaitalą. adresu , . Mes naudojame tęstinumo savybę (2):
.

Atlikime tą patį pakeitimą ir pritaikykime pirmą reikšmingą ribą (3):
.

Kadangi egzistuoja aukščiau apskaičiuotos ribos, taikome savybę (4):

.

Taigi mes gavome kosinuso išvestinės formulę.

Pavyzdžiai

Pasvarstykime paprasti pavyzdžiai funkcijų, turinčių kosinusą, išvestinių radimas. Raskime išvestinius iš šias funkcijas:
y = cos 2x; y = cos 3x; y = cos nx; y = cos 2x; y = cos 3x ir y = cos n x.

1 pavyzdys

Rasti išvestinius iš cos 2x, nes 3x Ir cosnx.

Sprendimas

Originalios funkcijos turi panašią formą. Todėl rasime funkcijos išvestinę y = cosnx. Tada kaip darinys iš cosnx, pakaitalas n = 2 ir n = 3 . Ir taip gauname išvestinių formules nes 2x Ir nes 3x .

Taigi, randame funkcijos išvestinę
y = cosnx .
Įsivaizduokime šią kintamojo x funkciją kaip sudėtingą funkciją, susidedančią iš dviejų funkcijų:
1)
2)
Tada pradinė funkcija yra sudėtinga (sudėtinė) funkcija, sudaryta iš funkcijų ir :
.

Raskime funkcijos išvestinę kintamojo x atžvilgiu:
.
Raskime funkcijos išvestinę kintamojo atžvilgiu:
.
Mes taikome.
.
Pakeiskime:
(P1) .

Dabar formulėje (A1) pakeičiame ir:
;
.

Atsakymas

;
;
.

2 pavyzdys

Raskite kosinuso kvadrato, kosinuso kubo ir kosinuso laipsnio n išvestines:
y = cos 2x; y = cos 3x; y = cos n x.

Sprendimas

Šiame pavyzdyje funkcijos taip pat atrodo panašiai. Todėl išvestinį rasime daugiausia bendroji funkcija- laipsnio n kosinusas:
y = cos n x.
Tada pakeičiame n = 2 ir n = 3. Taigi gauname kosinuso kvadrato ir kosinuso kubo išvestinių formules.

Taigi turime rasti funkcijos išvestinę
.
Perrašykime jį suprantamesne forma:
.
Įsivaizduokime šią funkciją kaip sudėtingą funkciją, susidedančią iš dviejų funkcijų:
1) Funkcijos, priklausančios nuo kintamojo: ;
2) Funkcijos, priklausančios nuo kintamojo: .
Tada pradinė funkcija yra sudėtinga funkcija, sudaryta iš dviejų funkcijų ir:
.

Raskite funkcijos išvestinę kintamojo x atžvilgiu:
.
Raskite funkcijos išvestinę kintamojo atžvilgiu:
.
Taikome sudėtingų funkcijų diferenciacijos taisyklę.
.
Pakeiskime:
(P2) .

Dabar pakeiskime ir:
;
.

Atsakymas

;
;
.

Aukštesnės eilės išvestinės priemonės

Atkreipkite dėmesį, kad vedinys iš cos x Pirmoji eilė gali būti išreikšta kosinusu taip:
.

Raskime antros eilės išvestinę naudodamiesi kompleksinės funkcijos išvestinės formule:

.
čia .

Atkreipkite dėmesį į skirtumą cos x sukelia jo argumento padidėjimą . Tada n-osios eilės išvestinė turi tokią formą:
(5) .

Šią formulę galima griežčiau įrodyti naudojant matematinės indukcijos metodą. Sinuso n-osios išvestinės įrodymas pateiktas puslapyje „Sinuso išvestinė“. N-osios kosinuso išvestinės įrodymas yra lygiai toks pat. Tiesiog visose formulėse nuodėmę reikia pakeisti cos.

Pateikiamos atvirkštinių trigonometrinių funkcijų išvestinės ir jų formulių išvedimas. Taip pat pateikiamos aukštesnės eilės išvestinių priemonių išraiškos. Nuorodos į puslapius su detalesniu formulių išvedimo aprašymu.

Pirmiausia išvedame arcsinuso išvestinės formulę. Leisti
y = arcsin x.
Kadangi arcsinusas yra atvirkštinė sinuso funkcija, tada
.
Čia y yra x funkcija. Atskirkite kintamąjį x:
.
Mes taikome:
.
Taigi mes radome:
.

Nes tada. Tada
.
Ir ankstesnė formulė yra tokia:
. Iš čia
.

Būtent tokiu būdu galite gauti lanko kosinuso išvestinės formulę. Tačiau lengviau naudoti formulę, susijusią su atvirkštinėmis trigonometrinėmis funkcijomis:
.
Tada
.

Išsamesnis aprašymas pateiktas puslapyje „Arkosino ir arkosino darinių dariniai“. Ten duota darinių išvedimas dviem būdais- aptarta aukščiau ir pagal atvirkštinės funkcijos išvestinės formulę.

Arktangento ir arkotangento darinių dariniai

Lygiai taip pat rasime arktangento ir arkotangento išvestinius.

Leisti
y = arctan x.
Arktangentas yra atvirkštinė liestinės funkcija:
.
Atskirkite kintamąjį x:
.
Taikome sudėtingos funkcijos išvestinės formulę:
.
Taigi mes radome:
.

Lanko kotangento išvestinė:
.

Arcino dariniai

Leisti
.
Mes jau radome pirmos eilės arcsinuso išvestinę:
.
Diferencijuodami randame antros eilės išvestinę:
;
.
Jis taip pat gali būti parašytas tokia forma:
.
Iš čia gauname diferencialinę lygtį, kurią tenkina pirmosios ir antrosios eilės arcsininės išvestinės:
.

Diferencijuodami šią lygtį galime rasti aukštesnės eilės išvestines.

N-osios eilės arcsinuso vedinys

n eilės arcsinuso išvestinė turi kitas vaizdas:
,
kur yra laipsnio daugianario . Jis nustatomas pagal formules:
;
.
čia .

Polinomas tenkina diferencialinę lygtį:
.

N-osios eilės arkosino vedinys

Lanko kosinuso išvestinės yra gaunamos iš lankinio sinuso išvestinių, naudojant trigonometrinę formulę:
.
Todėl šių funkcijų išvestiniai skiriasi tik ženklu:
.

Arktangento dariniai

Leisti . Mes radome pirmos eilės lankinio kotangento išvestinę:
.

Išskaidykime trupmeną į paprasčiausią formą:

.
Čia yra įsivaizduojamas vienetas, .

Atskiriame vieną kartą ir suvedame trupmeną į bendrą vardiklį:

.

Pakeisdami gauname:
.

N-osios eilės arctangento vedinys

Taigi n-osios eilės arctangento išvestinė gali būti pavaizduota keliais būdais:
;
.

Lanko kotangento dariniai

Tegul dabar būna. Taikykime atvirkštines trigonometrines funkcijas jungiančią formulę:
.
Tada n-osios eilės lanko liestinės išvestinė skiriasi tik ženklu nuo lanko liestinės išvestinės:
.

Pakeisdami randame:
.

Nuorodos:
N.M. Gunteris, R.O. Kuzminas, Aukštosios matematikos uždavinių rinkinys, „Lan“, 2003 m.

Rasti trigonometrinės funkcijos išvestinė reikia naudoti darinių lentelė, būtent išvestiniai 6-13.

Kai rasi paprastų trigonometrinių funkcijų išvestinės Norėdami išvengti įprastų klaidų, turėtumėte atkreipti dėmesį į šiuos dalykus:

• funkcijos išraiškoje vienas iš terminų dažnai yra sinuso, kosinuso ar kitos trigonometrinės funkcijos ne iš funkcijos argumento, o iš skaičiaus (konstantos), todėl šio nario išvestinė lygi nuliui;
• beveik visada reikia supaprastinti išraišką, gautą diferencijuojant, ir tam reikia užtikrintai naudotis žiniomis apie operacijas su trupmenomis;
• Norėdami supaprastinti posakį, beveik visada turite žinoti trigonometrinės tapatybės, pavyzdžiui, dvigubo kampo formulė ir vieneto formulė kaip sinuso ir kosinuso kvadratų suma.

1 pavyzdys. Raskite funkcijos išvestinę

Sprendimas. Tarkime su kosinuso vedinys viskas aišku, pasakys daugelis pradėjusių studijuoti darinius. Kaip apie sinuso vedinys dvylika padalinta iš pi? Atsakymas: laikykite jį lygiu nuliui! Čia sinusas (juk funkcija!) yra spąstai, nes argumentas yra ne kintamasis X ar bet koks kitas kintamasis, o tik skaičius. Tai yra, šio skaičiaus sinusas taip pat yra skaičius. O skaičiaus išvestinė (konstanta), kaip žinome iš išvestinių lentelės, lygi nuliui. Taigi, paliekame tik minusinį X sinusą ir randame jo išvestinę, nepamirštant ženklo:

.

2 pavyzdys. Raskite funkcijos išvestinę

.

Sprendimas. Antrasis terminas yra toks pat kaip ir pirmasis ankstesniame pavyzdyje. Tai yra, tai yra skaičius, o skaičiaus išvestinė yra nulis. Antrojo nario išvestinę randame kaip koeficiento išvestinę:

3 pavyzdys. Raskite funkcijos išvestinę

Sprendimas. Tai dar viena problema: čia pirmame naryje nėra arcsininės ar kitos trigonometinės funkcijos, bet yra x, vadinasi, tai yra x funkcija. Todėl išskiriame jį kaip terminą funkcijų sumoje:

Čia reikėjo įgūdžių atliekant operacijas su trupmenomis, būtent, pašalinti triaukštę trupmenos struktūrą.

4 pavyzdys. Raskite funkcijos išvestinę

.

Sprendimas. Čia raidė „phi“ atlieka tą patį vaidmenį kaip „x“ ankstesniais atvejais (ir daugeliu kitų, bet ne visais) – nepriklausomas kintamasis. Todėl, kai ieškosime funkcijų sandaugos išvestinės, neskubėsime „phi“ šaknies išvestinės skelbti lygia nuliui. Taigi:

Tačiau sprendimas tuo nesibaigia. Kadangi panašūs terminai surinkti dviejuose skliaustuose, vis tiek turime transformuoti (supaprastinti) išraišką. Todėl skliaustus padauginame iš už juos esančių veiksnių, tada terminus sujungiame į bendrą vardiklį ir atliekame kitas elementarias transformacijas:

5 pavyzdys. Raskite funkcijos išvestinę

Sprendimas. Šiame pavyzdyje turėsime žinoti faktą, kad yra tokia trigonometrinė funkcija – sekantas – ir jos formulės per kosinusą. Išskirkime:

6 pavyzdys. Raskite funkcijos išvestinę

.

Sprendimas. Šiame pavyzdyje turėsime prisiminti dvigubo kampo formulę iš mokyklos. Bet pirmiausia atskirkime:

,

(tai yra dvigubo kampo formulė)