Kokia yra pagrindinė logaritmo savybė? Logaritminės išraiškos. pavyzdžių

Logaritmo apibrėžimas

B logaritmas iki pagrindo a yra eksponentas, į kurį reikia pakelti a, kad gautume b.

Skaičius e matematikoje įprasta žymėti ribą, iki kurios išsireiškimas siekia

Skaičius e yra neracionalus skaičius- skaičius, nesuderinamas su vienu, jo negalima tiksliai išreikšti nei sveikuoju skaičiumi, nei trupmena racionalus numerį.

Laiškas e- pirmoji raidė Lotyniškas žodis exponere- pasipuikuoti, iš čia ir toks pavadinimas matematikoje eksponentinis - eksponentinė funkcija.

Skaičius e plačiai naudojami matematikoje ir visuose moksluose, kurie vienaip ar kitaip savo reikmėms naudoja matematinius skaičiavimus.

Logaritmai. Logaritmų savybės

Apibrėžimas: teigiamo skaičiaus b logaritmas iki jo bazės yra eksponentas c, iki kurio reikia pakelti skaičių a, kad gautume skaičių b.

Pagrindinė logaritminė tapatybė:

7) Persikėlimo į naują bazę formulė:

lna = log e a, e ≈ 2,718…

Uždaviniai ir testai tema „Logaritmai. Logaritmų savybės"

• Logaritmai – svarbios temos peržiūrint vieningą valstybinį matematikos egzaminą

Norėdami sėkmingai atlikti užduotis šia tema, turite žinoti logaritmo apibrėžimą, logaritmų savybes, pagrindinę logaritminę tapatybę, dešimtainių ir natūraliųjų logaritmų apibrėžimus. Pagrindinės šios temos problemų rūšys yra logaritminių išraiškų skaičiavimo ir transformavimo problemos. Panagrinėkime jų sprendimą naudodamiesi šiais pavyzdžiais.

Sprendimas: Pasinaudoję logaritmų savybėmis gauname

Sprendimas: Naudodamiesi laipsnių savybėmis gauname

1) (2 2) log 2 5 = (2 log 2 5) 2 = 5 2 =25

Logaritmų, formuluočių ir įrodymų savybės.

Logaritmai turi keletą būdingų savybių. Šiame straipsnyje apžvelgsime pagrindinius logaritmų savybės. Čia pateiksime jų formuluotes, surašysime logaritmų savybes formulių pavidalu, parodysime jų taikymo pavyzdžius, taip pat pateiksime logaritmų savybių įrodymą.

Puslapio naršymas.

Pagrindinės logaritmų savybės, formulės

Kad būtų lengviau atsiminti ir naudoti, įsivaizduokime Pagrindinės logaritmų savybės formulių sąrašo pavidalu. Kitoje pastraipoje pateiksime jų formuluotes, įrodymus, naudojimo pavyzdžius ir būtinus paaiškinimus.

Vienybės logaritmo savybė: log a 1=0 bet kuriam a>0, a≠1.

Skaičiaus, lygaus bazei, logaritmas: loga a a=1, kai a>0, a≠1.

Pagrindo laipsnio logaritmo savybė: log a a p =p, kur a>0, a≠1 ir p – bet koks tikras numeris.

Dviejų teigiamų skaičių sandaugos logaritmas: log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 ,
ir n teigiamų skaičių sandaugos logaritmo savybė: log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n , a>0 , a≠1 , x 1 >0, x 2 >0, …, x n >0 .

Dalinio logaritmo savybė: , kur a>0, a≠1, x>0, y>0.

Skaičiaus laipsnio logaritmas: log a b p =p·log a |b| , kur a>0, a≠1, b ir p yra tokie skaičiai, kad b p laipsnis turi prasmę, o b p >0.

Pasekmė: , kur a>0, a≠1, n yra natūralusis skaičius, didesnis už vienetą, b>0.

1 išvada: , a>0, a≠1, b>0, b≠1.

2 išvada: , a>0, a≠1, b>0, p ir q yra realieji skaičiai, q≠0, ypač jei b=a .

Savybių formuluotės ir įrodymai

Mes pereiname prie logaritmų rašytinių savybių formulavimo ir įrodymo. Visos logaritmų savybės yra įrodytos remiantis logaritmo apibrėžimu ir iš jo išplaukiančiu pagrindiniu logaritminiu tapatumu, taip pat laipsnio savybėmis.

Pradėkime nuo vieneto logaritmo savybės. Jo formuluotė yra tokia: vienybės logaritmas lygus nuliui, tai yra, log a 1=0 bet kuriam a>0, a≠1. Įrodymas nėra sudėtingas: kadangi a 0 =1 bet kuriai a, tenkinančiai aukščiau nurodytas sąlygas a>0 ir a≠1, tai įrodinėtina lygybė log a 1=0 iš karto išplaukia iš logaritmo apibrėžimo.

Pateiksime nagrinėjamos savybės taikymo pavyzdžius: log 3 1=0, log1=0 ir .

Pereikime prie kitos nuosavybės: skaičiaus, lygaus bazei, logaritmas lygus vienetui, tai yra, log a a=1 jei a>0, a≠1. Iš tiesų, kadangi a 1 =a bet kuriam a, tai pagal logaritmo apibrėžimą log a a = 1.

Šios logaritmų savybės panaudojimo pavyzdžiai yra lygybės log 5 5=1, log 5.6 5.6 ir lne=1.

Skaičiaus, lygaus logaritmo pagrindui, laipsnio logaritmas yra lygus eksponentui. Ši logaritmo savybė atitinka formos formulę log a a p =p, kur a>0, a≠1 ir p – bet koks realusis skaičius. Ši savybė tiesiogiai išplaukia iš logaritmo apibrėžimo. Atkreipkite dėmesį, kad tai leidžia iš karto nurodyti logaritmo reikšmę, jei skaičių po logaritmo ženklu galima pavaizduoti kaip bazės laipsnį; plačiau apie tai kalbėsime straipsnyje apie logaritmų skaičiavimą.

Pavyzdžiui, log 2 2 7 =7, log10 -4 =-4 ir .

Dviejų teigiamų skaičių sandaugos logaritmas x ir y yra lygūs šių skaičių logaritmų sandaugai: log a (x y)=log a x+log a y, a>0 , a≠1 . Įrodykime sandaugos logaritmo savybę. Dėl laipsnio savybių a log a x+log a y =a log a x ·a log a y, o kadangi pagal pagrindinę logaritminę tapatybę log a x =x ir log a y =y, tada log a x ·a log a y =x· y. Taigi log a x+log a y =x·y, iš kurio pagal logaritmo apibrėžimą išplaukia įrodoma lygybė.

Parodykime gaminio logaritmo savybės panaudojimo pavyzdžius: log 5 (2 3)=log 5 2+log 5 3 ir .

Produkto logaritmo savybę galima apibendrinti baigtinio skaičiaus n teigiamų skaičių x 1 , x 2 , …, x n sandaugai kaip log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n. Šią lygybę galima be problemų įrodyti naudojant matematinės indukcijos metodą.

Pavyzdžiui, sandaugos natūralusis logaritmas gali būti pakeistas trijų skaičių 4, e ir natūraliųjų logaritmų suma.

Dviejų teigiamų skaičių dalinio logaritmas x ir y yra lygus šių skaičių logaritmų skirtumui. Dalinio logaritmo savybė atitinka formos formulę , kur a>0, a≠1, x ir y yra kai kurie teigiami skaičiai. Šios formulės pagrįstumas įrodytas kaip ir sandaugos logaritmo formulė: kadangi , tada pagal logaritmo apibrėžimą .

Štai šios logaritmo savybės naudojimo pavyzdys: .

Pereikime prie galios logaritmo savybė. Laipsnio logaritmas lygus eksponento sandaugai ir šio laipsnio pagrindo modulio logaritmui. Parašykime šią laipsnio logaritmo savybę kaip formulę: log a b p =p·log a |b|, kur a>0, a≠1, b ir p yra tokie skaičiai, kad b p laipsnis turi prasmę, o b p >0.

Pirmiausia įrodome šią savybę teigiamam b. Pagrindinė logaritminė tapatybė leidžia pavaizduoti skaičių b kaip log a b , tada b p =(a log a b) p , o gauta išraiška dėl galios savybės yra lygi a p·log a b . Taigi gauname lygybę b p =a p·log a b, iš kurios pagal logaritmo apibrėžimą darome išvadą, kad log a b p =p·log a b.

Belieka įrodyti šią savybę neigiamam b. Čia pažymime, kad reiškinys log a b p neigiamam b turi prasmę tik lyginiams eksponentams p (kadangi laipsnio b p reikšmė turi būti didesnė už nulį, antraip logaritmas neturės prasmės), o šiuo atveju b p =|b| p. Tada b p =|b| p =(a log a |b|) p =a p·log a |b| , iš kur log a b p =p·log a |b| .

Pavyzdžiui, ir ln(-3) 4 =4·ln|-3|=4·ln3 .

Tai išplaukia iš ankstesnio turto logaritmo savybė nuo šaknies: n-osios šaknies logaritmas yra lygus trupmenos 1/n sandaugai iš radikalios išraiškos logaritmo, tai yra, kur a>0, a≠1, n yra natūralusis skaičius, didesnis už vienetą, b>0 .

Įrodymas pagrįstas lygybe (žr. eksponento su trupmeniniu rodikliu apibrėžimą), kuri galioja bet kuriam teigiamam b, ir eksponento logaritmo savybe: .

Štai šios nuosavybės naudojimo pavyzdys: .

Dabar įrodykime perėjimo prie naujos logaritmo bazės formulė malonus . Tam pakanka įrodyti lygybės log c b=log a b·log c a pagrįstumą. Pagrindinė logaritminė tapatybė leidžia mums pavaizduoti skaičių b kaip log a b , tada log c b=log c a log a b . Belieka naudoti laipsnio logaritmo savybę: log c a log a b =log a b·log c a . Tai įrodo lygybę log c b=log a b·log c a, o tai reiškia, kad taip pat įrodyta perėjimo prie naujos logaritmo bazės formulė .

Parodykime keletą šios logaritmų savybės naudojimo pavyzdžių: ir .

Perėjimo prie naujos bazės formulė leidžia pereiti prie darbo su logaritmais, kurie turi „patogų“ pagrindą. Pavyzdžiui, jį galima naudoti norint pakeisti natūraliuosius arba dešimtainius logaritmus, kad galėtumėte apskaičiuoti logaritmo reikšmę iš logaritmų lentelės. Perėjimo prie naujos logaritmo bazės formulė taip pat leidžia kai kuriais atvejais rasti tam tikro logaritmo reikšmę, kai žinomos kai kurių logaritmų su kitomis bazėmis reikšmės.

Dažnai naudojamas specialus perėjimo prie naujos logaritmo bazės formulės atvejis, kai formos c=b. Tai rodo, kad log a b ir log b a yra tarpusavyje atvirkštiniai skaičiai. Pvz., .

Taip pat dažnai naudojama formulė, kuri yra patogu ieškant logaritmų reikšmių. Norėdami patvirtinti savo žodžius, parodysime, kaip jį galima naudoti apskaičiuojant formos logaritmo reikšmę. Mes turime . Norėdami įrodyti formulę, pakanka naudoti formulę, skirtą pereiti prie naujos logaritmo bazės a: .

Belieka įrodyti logaritmų palyginimo savybes.

Naudokime priešingą metodą. Tarkime, kad a 1 >1, a 2 >1 ir a 1 2 ir 0 1 log a 1 b≤log a 2 b yra teisinga. Remiantis logaritmų savybėmis, šias nelygybes galima perrašyti kaip Ir atitinkamai, o iš jų išplaukia, kad atitinkamai log b a 1 ≤log b a 2 ir log b a 1 ≥log b a 2. Tada pagal tų pačių bazių laipsnių savybes turi galioti lygybės b log b a 1 ≥b log b a 2 ir b log b a 1 ≥b log b a 2, tai yra a 1 ≥a 2 . Taigi mes priėjome prietarą sąlygai a 1 2. Tai užbaigia įrodymą.

Pagrindinės logaritmų savybės

• Medžiaga pamokai
• Parsisiųsti visas formules

Logaritmus, kaip ir bet kokius skaičius, galima visais būdais sudėti, atimti ir transformuoti. Bet kadangi logaritmai nėra visiškai įprasti skaičiai, čia yra taisyklės, kurios vadinamos pagrindinės savybės.

Jūs tikrai turite žinoti šias taisykles – be jų nepavyks išspręsti nė vienos rimtos logaritminės problemos. Be to, jų labai mažai – viską gali išmokti per vieną dieną. Taigi pradėkime.

Logaritmų pridėjimas ir atėmimas

Apsvarstykite du logaritmus su tais pačiais pagrindais: log a x ir log a y. Tada juos galima pridėti ir atimti, ir:

Taigi logaritmų suma lygi sandaugos logaritmui, o skirtumas lygus koeficiento logaritmui. Pastaba: pagrindinis momentasČia - identiškais pagrindais. Jei priežastys skiriasi, šios taisyklės neveikia!

Šios formulės padės apskaičiuoti logaritminę išraišką net tada, kai neatsižvelgiama į atskiras jos dalis (žr. pamoką „Kas yra logaritmas“). Pažvelkite į pavyzdžius ir pamatykite:

Užduotis. Raskite išraiškos reikšmę: log 6 4 + log 6 9.

Kadangi logaritmai turi tas pačias bazes, naudojame sumos formulę:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Užduotis. Raskite išraiškos reikšmę: log 2 48 − log 2 3.

Pagrindai yra vienodi, mes naudojame skirtumo formulę:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Užduotis. Raskite išraiškos reikšmę: log 3 135 − log 3 5.

Vėlgi bazės yra tos pačios, todėl turime:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Kaip matote, pradinės išraiškos yra sudarytos iš „blogų“ logaritmų, kurie nėra skaičiuojami atskirai. Tačiau po transformacijų jie pasirodo gana normalūs skaičiai. Daugelis remiasi šiuo faktu bandomieji darbai. Taip, vieningo valstybinio egzamino metu į testus panašūs posakiai siūlomi labai rimtai (kartais praktiškai be pakeitimų).

Rodiklio išskyrimas iš logaritmo

Dabar šiek tiek apsunkinkime užduotį. Ką daryti, jei logaritmo pagrindas arba argumentas yra laipsnis? Tada šio laipsnio rodiklis gali būti paimtas iš logaritmo ženklo pagal šias taisykles:

• log a x n = n · log a x ;
• 
• 

Nesunku pastebėti, kad paskutinė taisyklė seka pirmąsias dvi. Bet vis tiek geriau tai atsiminti - kai kuriais atvejais tai žymiai sumažins skaičiavimų skaičių.

Žinoma, visos šios taisyklės turi prasmę, jei laikomasi logaritmo ODZ: a > 0, a ≠ 1, x > 0. Ir dar vienas dalykas: išmokite taikyti visas formules ne tik iš kairės į dešinę, bet ir atvirkščiai , t.y. Skaičius prieš logaritmo ženklą galite įvesti į patį logaritmą. Tai yra tai, ko dažniausiai reikia.

Užduotis. Raskite išraiškos reikšmę: log 7 49 6 .

Atsikratykime argumento laipsnio naudodami pirmąją formulę:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Užduotis. Raskite posakio prasmę:

[Paveikslo antraštė]

Atkreipkite dėmesį, kad vardiklyje yra logaritmas, kurio pagrindas ir argumentas yra tikslieji laipsniai: 16 = 2 4 ; 49 = 7 2. Mes turime:

[Paveikslo antraštė]

Manau, kad paskutinis pavyzdys reikalauja šiek tiek paaiškinimo. Kur dingo logaritmai? Iki pat paskutinės akimirkos dirbame tik su vardikliu. Pateikėme ten stovinčio logaritmo bazę ir argumentą galių pavidalu ir išėmėme eksponentus - gavome „trijų aukštų“ trupmeną.

Dabar pažvelkime į pagrindinę dalį. Skaitiklyje ir vardiklyje yra tas pats skaičius: log 2 7. Kadangi log 2 7 ≠ 0, tai trupmeną galime sumažinti – vardiklyje liks 2/4. Pagal aritmetikos taisykles keturis galima perkelti į skaitiklį, kas buvo padaryta. Rezultatas buvo atsakymas: 2.

Perėjimas prie naujo pagrindo

Kalbėdamas apie logaritmų sudėjimo ir atėmimo taisykles, konkrečiai pabrėžiau, kad jos veikia tik su tais pačiais pagrindais. O jei priežastys kitokios? O jei jie nėra tikslūs to paties skaičiaus laipsniai?

Į pagalbą ateina perėjimo prie naujo pagrindo formulės. Suformuluokime juos teoremos forma:

Tegu pateiktas logaritmas log a x. Tada bet kurio skaičiaus c, kurio c > 0 ir c ≠ 1, lygybė yra teisinga:

[Paveikslo antraštė]

Konkrečiai, jei nustatome c = x, gauname:

[Paveikslo antraštė]

Iš antrosios formulės išplaukia, kad logaritmo bazę ir argumentą galima sukeisti vietomis, tačiau tokiu atveju „apverčiama“ visa išraiška, t.y. vardiklyje atsiranda logaritmas.

Šios formulės retai sutinkamos įprastose skaitinės išraiškos. Įvertinti, kiek jos patogios, galima tik sprendžiant logaritmines lygtis ir nelygybes.

Tačiau yra problemų, kurių niekaip nepavyks išspręsti, išskyrus persikėlimą į naują fondą. Pažvelkime į porą iš šių:

Užduotis. Raskite išraiškos reikšmę: log 5 16 log 2 25.

Atkreipkite dėmesį, kad abiejų logaritmų argumentuose yra tikslios galios. Išimkime rodiklius: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2 log 2 5;

Dabar „apverskime“ antrąjį logaritmą:

[Paveikslo antraštė]

Kadangi sandauga nesikeičia pertvarkant veiksnius, ramiai padauginome keturis ir du, o tada nagrinėjome logaritmus.

Užduotis. Raskite išraiškos reikšmę: log 9 100 lg 3.

Pirmojo logaritmo pagrindas ir argumentas yra tikslios galios. Užsirašykime tai ir atsikratykime rodiklių:

[Paveikslo antraštė]

Dabar atsikratykime dešimtainio logaritmo, pereidami prie naujos bazės:

[Paveikslo antraštė]

Pagrindinė logaritminė tapatybė

Dažnai sprendimo procese skaičių reikia pateikti kaip logaritmą tam tikram pagrindui. Šiuo atveju mums padės šios formulės:

1. n = log a a n

2. Pirmuoju atveju skaičius n tampa veiksniu argumente. Skaičius n gali būti visiškai bet koks, nes tai tik logaritmo reikšmė.

   Antroji formulė iš tikrųjų yra perfrazuotas apibrėžimas. Taip ji vadinama: pagrindinė logaritminė tapatybė.

   Tiesą sakant, kas atsitiks, jei skaičius b padidintas iki tokios laipsnio, kad skaičius b iki šios laipsnio duotų skaičių a? Teisingai: rezultatas yra tas pats skaičius a. Dar kartą atidžiai perskaitykite šią pastraipą – daugeliui žmonių ji įstrigo.

   Kaip ir formulės, skirtos pereiti prie naujos bazės, pagrindinė logaritminė tapatybė kartais yra vienintelis galimas sprendimas.

   [Paveikslo antraštė]

   Atkreipkite dėmesį, kad log 25 64 = log 5 8 - mes tiesiog paėmėme kvadratą iš logaritmo pagrindo ir argumento. Atsižvelgdami į galių dauginimo su ta pačia baze taisykles, gauname:

   [Paveikslo antraštė]

   Jei kas nežino, tai buvo tikra užduotis iš unifikuoto valstybinio egzamino :)

   Logaritminis vienetas ir logaritminis nulis

   Baigdamas pateiksiu dvi tapatybes, kurias vargu ar galima pavadinti savybėmis – veikiau tai yra logaritmo apibrėžimo pasekmės. Jie nuolat atsiranda problemų ir, stebėtinai, sukelia problemų net „pažengusiems“ studentams.

   1. log a a = 1 yra logaritminis vienetas. Vieną kartą ir visiems laikams atsiminkite: logaritmas bet kuriam tos bazės pagrindui a yra lygus vienetui.
   2. log a 1 = 0 yra logaritminis nulis. Bazė a gali būti bet kokia, bet jei argumente yra vienas, logaritmas lygus nuliui! Kadangi a 0 = 1 yra tiesioginė apibrėžimo pasekmė.

   Tai visos savybės. Būtinai praktikuokite juos pritaikydami praktiškai! Pamokos pradžioje atsisiųskite cheat lapą, atsispausdinkite ir išspręskite problemas.

   Logaritmas. Logaritmo savybės (sudėti ir atimti).

   Logaritmo savybės išplaukia iš jo apibrėžimo. Ir taip skaičiaus logaritmas b remiantis A apibrėžiamas kaip eksponentas, iki kurio skaičius turi būti padidintas a norėdami gauti numerį b(logaritmas egzistuoja tik teigiamiems skaičiams).

   Iš šios formuluotės matyti, kad skaičiavimas x=log a b, yra lygiavertis lygties sprendimui a x =b. Pavyzdžiui, log 2 8 = 3 nes 8 = 2 3 . Logaritmo formuluotė leidžia pagrįsti, kad jeigu b=a c, tada skaičiaus logaritmas b remiantis a lygus Su. Taip pat aišku, kad logaritmų tema yra glaudžiai susijusi su galių tema.

   Su logaritmais, kaip ir su bet kuriais skaičiais, galite tai padaryti sudėjimo, atimties operacijos ir transformuotis visais įmanomais būdais. Tačiau dėl to, kad logaritmai nėra visiškai įprasti skaičiai, čia galioja savos specialios taisyklės, kurios vadinamos pagrindinės savybės.

   Logaritmų pridėjimas ir atėmimas.

   Paimkime du logaritmus su tomis pačiomis bazėmis: užsirašyk x Ir prisijungti a y. Tada galima atlikti sudėjimo ir atimties operacijas:

   Kaip matome, logaritmų suma lygus sandaugos logaritmui ir skirtumas logaritmus- koeficiento logaritmas. Be to, tai tiesa, jei skaičiai A, X Ir adresu teigiamas ir a ≠ 1.

   Svarbu pažymėti, kad pagrindinis šių formulių aspektas yra tos pačios bazės. Jei priežastys skiriasi, šios taisyklės netaikomos!

   Logaritmų su tais pačiais pagrindais sudėties ir atėmimo taisyklės skaitomos ne tik iš kairės į dešinę, bet ir atvirkščiai. Dėl to turime sandaugos logaritmo ir koeficiento logaritmo teoremas.

   Produkto logaritmas du teigiami skaičiai lygi sumai jų logaritmus ; perfrazuodami šią teoremą gauname taip, jei skaičiai A, x Ir adresu teigiamas ir a ≠ 1, Tai:

   Dalinio logaritmas du teigiami skaičiai yra lygūs skirtumui tarp dividendo ir daliklio logaritmų. Kitaip tariant, jei skaičiai A, X Ir adresu teigiamas ir a ≠ 1, Tai:

   Sprendimui pritaikykime aukščiau pateiktas teoremas pavyzdžių:

   Jei skaičiai x Ir adresu tada yra neigiami produkto logaritmo formulė tampa beprasmis. Todėl draudžiama rašyti:

   nes išraiškos log 2 (-8) ir log 2 (-4) iš viso neapibrėžtos (logaritminė funkcija adresu= 2 žurnalas X apibrėžta tik teigiamas vertes argumentas X).

   Produkto teorema taikomas ne tik dviem, bet ir neribotam skaičiui veiksnių. Tai reiškia, kad kiekvienam natūraliam k ir bet kokie teigiami skaičiai x 1 , x 2 , . . . ,x n yra tapatybė:

   Iš logaritmo koeficiento teorema Galima gauti dar vieną logaritmo savybę. Visiems žinoma, kad žurnalas a 1 = 0, todėl

   Tai reiškia, kad yra lygybė:

   Dviejų tarpusavio logaritmai abipusiai skaičiai dėl tos pačios priežasties vienas nuo kito skirsis tik ženklu. Taigi:

   Logaritmas. Logaritmų savybės

   Logaritmas. Logaritmų savybės

   Pasvarstykime apie lygybę. Leiskite mums žinoti ir vertes ir mes norime rasti vertę.

   Tai yra, mes ieškome eksponento, pagal kurį turime jį pakelti, kad gautume .

   Leisti kintamasis gali įgyti bet kokią realią reikšmę, tada kintamiesiems taikomi šie apribojimai: o" title="a>o"/> , 1″ title="a1″/>, 0″ title="b>0″ />

   Jei žinome ir reikšmes ir susiduriame su užduotimi surasti nežinomybę, tai tam tikslui įvedamas matematinis veiksmas, kuris vadinamas logaritmas.

   Norėdami rasti vertę, kurią gauname skaičiaus logaritmas Autorius pagrindu :

   Skaičiaus logaritmas iki jo bazės yra eksponentas, iki kurio jis turi būti padidintas, kad gautų .

   Tai yra pagrindinė logaritminė tapatybė:

   o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>

   iš esmės yra matematinis žymėjimas logaritmo apibrėžimai.

   Matematinis logaritmo veiksmas yra atvirkštinis eksponencijos veiksmas, taigi logaritmų savybės yra glaudžiai susiję su laipsnio savybėmis.

   Išvardinkime pagrindinius logaritmų savybės:

   (o" title="a>o"/> , 1″ title=»a1″/>, 0″ title=»b>0″/>, 0,

   d>0″/>, 1″ title=”d1″/>

   4.

   5.

   Ši savybių grupė leidžia pavaizduoti išraiškos eksponentą po logaritmo ženklu arba stovint logaritmo pagrindu koeficiento pavidalu prieš logaritmo ženklą:

   6.

   7.

   8.

   9.

   Kita formulių grupė leidžia pereiti nuo logaritmo su duota baze prie logaritmo su savavališka baze ir yra vadinama perėjimo prie naujos bazės formulės:

   10.

   12. (11 nuosavybės pasekmė)

   

   Šios trys savybės nėra gerai žinomos, tačiau jos dažnai naudojamos sprendžiant logaritmines lygtis arba supaprastinant logaritmų turinčias išraiškas:

   13.

   14.

   15.

   Ypatingi atvejai:

   — dešimtainis logaritmas

   — natūralusis logaritmas

   Supaprastinant išraiškas, kuriose yra logaritmų, naudojamas bendras metodas:

   1. Pristatome po kablelio paprastų pavidalu.

   2. Mišrius skaičius pavaizduojame kaip netinkamąsias trupmenas.

   3. Skaičius logaritmo pagrindu ir po logaritmo ženklu išskaidome į paprastus veiksnius.

   4. Visus logaritmus stengiamės sumažinti iki tos pačios bazės.

   5. Taikyti logaritmų savybes.

   Pažvelkime į logaritmų turinčių išraiškų supaprastinimo pavyzdžius.

   1 pavyzdys.

   Apskaičiuoti:

   Supaprastinkime visus laipsnius: mūsų užduotis yra sumažinti juos iki logaritmų, kurių bazė yra tokia pati kaip ir eksponento bazė.

   ==(pagal 7 savybę)=(pagal 6 savybę) =

   Pakeiskime rodiklius, kuriuos gavome į pradinę išraišką. Mes gauname:

   Atsakymas: 5.25

   2 pavyzdys. Apskaičiuokite:

   

   Sumažinkime visus logaritmus iki 6 bazės (šiuo atveju logaritmai iš trupmenos vardiklio „perkels“ į skaitiklį):

   Išskaidykime skaičius po logaritmo ženklu į paprastus veiksnius:

   Taikykime 4 ir 6 savybes:

   Pristatome pakaitalą

   Mes gauname:

   Atsakymas: 1

   Logaritmas . Pagrindinė logaritminė tapatybė.

   Logaritmų savybės. Dešimtainis logaritmas. Natūralus logaritmas.

   Logaritmas teigiamas skaičius N į bazę (b > 0, b 1) yra eksponentas x, iki kurio b reikia pakelti, kad gautume N .

   Šis įrašas atitinka šį: b x = N .

   Pavyzdžiai: log 3 81 = 4, nes 3 4 = 81;

   log 1/3 27 = – 3, nes (1/3) – 3 = 3 3 = 27.

   Aukščiau pateiktas logaritmo apibrėžimas gali būti parašytas kaip tapatybė:

   

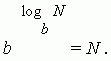
   Pagrindinės logaritmų savybės.

   2) log 1 = 0, nes b 0 = 1 .

   3) Produkto logaritmas yra lygus faktorių logaritmų sumai:

   4) Dalinio logaritmas yra lygus skirtumui tarp dividendo ir daliklio logaritmų:

   5) Laipsnio logaritmas lygus eksponento sandaugai ir jo bazės logaritmui:

   Šios nuosavybės pasekmės yra šios: šaknies logaritmas lygus radikalinio skaičiaus logaritmui, padalytam iš šaknies galios:

   

   6) Jei logaritmo pagrindas yra laipsnis, tada reikšmė atvirkštinį rodiklį galima paimti kaip loginį rimą:

   

   Paskutinės dvi savybės gali būti sujungtos į vieną:

   

   7) Perėjimo modulio formulė (t. y. perėjimas iš vienos logaritmo bazės į kitą):

   

   Ypatingu atveju, kai N=a mes turime:

   

   Dešimtainis logaritmas paskambino bazinis logaritmas 10. Žymima lg, t.y. žurnalas 10 N= žurnalas N. Skaičių 10, 100, 1000, logaritmai. p yra atitinkamai 1, 2, 3, …, t.y. turi tiek daug teigiamo

   vienetų, kiek nulių yra logaritminiame skaičiuje po vieneto. Skaičių logaritmai 0,1, 0,01, 0,001, . p yra atitinkamai –1, –2, –3, …, t.y. turėti tiek neigiamų, kiek logaritminiame skaičiuje prieš vieną yra nulių (įskaitant nulius sveikųjų skaičių). Kitų skaičių logaritmai turi trupmeninę dalį, vadinamą mantisa. Visa dalis vadinamas logaritmas charakteristika. Praktiniam naudojimui patogiausias yra dešimtainis logaritmas.

   Natūralus logaritmas paskambino bazinis logaritmas e. Ji žymima ln, t.y. žurnalas e N= žurnalas N. Skaičius e yra neracionalus, jo apytikslė reikšmė yra 2,718281828. Tai riba, iki kurios linkęs skaičius (1 + 1 / n) n su neribotu padidėjimu n(cm. pirmoji nuostabi riba puslapyje „Skaičių sekos ribos“).
   Kad ir kaip būtų keista, natūralūs logaritmai pasirodė labai patogūs atliekant įvairaus pobūdžio operacijas, susijusias su funkcijų analize. Logaritmų skaičiavimas į bazę e atlikti daug greičiau nei dėl bet kokios kitos priežasties.

• Kaip gauti buto nuosavybės valstybinės registracijos pažymėjimą? Pagal Rusijos Federacijos Konstituciją valstybei patikėta privačios nuosavybės teisių garanto funkcija. Valstybės galios šioje srityje […]
• Kampai ir centrai grupėse Kampai – skyrius, kuriame įdomių idėjų ir dizaino parinktys informaciniams, vystomiesiems ir žaidimų kampams darželis, pagamintas mokytojų ir auklėtojų rankomis. Ikimokyklinio ugdymo įstaigos grupėje, priklausomai nuo [...]
• Ko šiandien reikia norint įvaikinti vaiką Rusijoje? Įvaikinimas Rusijoje, be atsakingo asmeninio sprendimo, apima daugybę kandidatų valstybinio patikrinimo procedūrų. Griežta atranka parengiamajame etape prisideda prie daugiau […]
• Bauda už ataskaitų SZV-M ir RSV-1 nepateikimą Rusijos Federacijos pensijų fondui Kiekvieno ataskaitinio ir atsiskaitymo laikotarpio pabaigoje draudėjas privalo pateikti Pensijų fondas būtiną skaičiavimą pagal RSV-1 formą. Jei dėl kokių nors priežasčių […]
• Kada ir kaip gauti finansuojamą pensijos dalį iš „Sberbank“? „Sberbank“ yra valstybinio pensijų fondo bankas partneris. Remiantis tuo, piliečiai, užsiregistravę gauti pensijų kaupimą, galėjo pervesti kaupiamąją dalį […]
• Kaip gauti subsidijas mokėjimui Komunalinės paslaugos(nuoma)? Subsidijos už komunalines paslaugas teikiamos tam tikroms piliečių kategorijoms pagal Rusijos Federacijos būsto įstatymus. Norėdami sužinoti daugiau apie procedūrą [...]
• Nemokama informacija TIN arba OGRN iš mokesčių registro visoje Rusijoje - internete Vienintelis portalas Mokesčių tarnybos gali gauti informaciją apie valstybinę registraciją juridiniai asmenys, individualūs verslininkai, […]
• Cesspool: sanitariniai ir statybos kodeksai ir taisyklės Norėdami įrengti kanalizacijos sistemą vasarnamyje ar miesto teritorijoje, turite laikytis ne tik statybos, bet ir teisės aktų standartų. Cesspool: normos ir jos išdėstymo taisyklės [...]

Palyginti su

galima nustatyti užduotį surasti bet kurį iš trijų skaičių iš kitų dviejų pateiktų. Jei duoti a ir tada N, jie randami eksponencijos būdu. Jei N ir tada a yra duoti paėmus x laipsnio šaknį (arba pakėlus jį į laipsnį). Dabar apsvarstykite atvejį, kai, esant a ir N, turime rasti x.

Tegul skaičius N yra teigiamas: skaičius a yra teigiamas ir nėra lygus vienetui: .

Apibrėžimas. Skaičiaus N logaritmas iki pagrindo a yra eksponentas, iki kurio reikia pakelti a, kad gautume skaičių N; logaritmas žymimas

Taigi lygybėje (26.1) eksponentas randamas kaip N logaritmas bazei a. Įrašai

turi tą pačią reikšmę. Lygybė (26.1) kartais vadinama pagrindine logaritmų teorijos tapatybe; tikrovėje išreiškia logaritmo sąvokos apibrėžimą. Autorius šis apibrėžimas Logaritmo a pagrindas visada yra teigiamas ir skiriasi nuo vienybės; logaritminis skaičius N yra teigiamas. Neigiami skaičiai ir nulis neturi logaritmų. Galima įrodyti, kad bet kuris skaičius, turintis tam tikrą bazę, turi tiksliai apibrėžtą logaritmą. Todėl lygybė reiškia. Atkreipkite dėmesį, kad sąlyga čia yra esminė; priešingu atveju išvada nebūtų pagrįsta, nes lygybė galioja bet kurioms x ir y reikšmėms.

1 pavyzdys. Rasti

Sprendimas. Norėdami gauti skaičių, turite pakelti bazę 2 iki galios Todėl.

Spręsdami tokius pavyzdžius galite užsirašyti tokia forma:

2 pavyzdys. Rasti .

Sprendimas. Mes turime

1 ir 2 pavyzdžiuose nesunkiai radome norimą logaritmą, pateikdami logaritmo skaičių kaip pagrindo laipsnį su racionaliuoju eksponentu. Bendruoju atveju, pavyzdžiui, ir pan., to padaryti negalima, nes logaritmas turi neracionalią reikšmę. Atkreipkime dėmesį į vieną su šiuo teiginiu susijusį klausimą. 12 pastraipoje mes pateikėme galimybę nustatyti bet kurią tikrosios tam tikro teigiamo skaičiaus galią. Tai buvo būtina norint įvesti logaritmus, kurie paprastai gali būti neracionalūs skaičiai.

Pažvelkime į kai kurias logaritmų savybes.

Savybė 1. Jeigu skaičius ir bazė lygūs, tai logaritmas lygus vienetui, ir atvirkščiai, jei logaritmas lygus vienetui, tai skaičius ir bazė yra lygūs.

Įrodymas. Tegul Pagal logaritmo apibrėžimą turime ir iš kur

Ir atvirkščiai, tegul Tada pagal apibrėžimą

Savybė 2. Vieneto logaritmas bet kokiam pagrindui lygus nuliui.

Įrodymas. Pagal logaritmo apibrėžimą (bet kurio teigiamo pagrindo nulinė galia lygi vienetui, žr. (10.1)). Iš čia

Q.E.D.

Taip pat teisingas ir atvirkštinis teiginys: jei , tada N = 1. Iš tiesų, mes turime .

Prieš formuluodami kitą logaritmų savybę, susitarkime, kad du skaičiai a ir b yra toje pačioje trečiojo skaičiaus c pusėje, jei jie abu yra didesni už c arba mažesni už c. Jei vienas iš šių skaičių yra didesnis nei c, o kitas mažesnis už c, tada sakysime, kad jie yra kartu skirtingos pusės iš kaimo

Savybė 3. Jei skaičius ir bazė yra toje pačioje pusėje, tada logaritmas yra teigiamas; Jei skaičius ir bazė yra priešingose ​​vieneto pusėse, tada logaritmas yra neigiamas.

3 savybės įrodymas grindžiamas tuo, kad a galia yra didesnė už vienetą, jei bazė yra didesnė už vieną, o rodiklis yra teigiamas arba bazė yra mažesnė už vieną, o rodiklis yra neigiamas. Laipsnis yra mažesnis už vieną, jei bazė yra didesnė už vieną, o rodiklis yra neigiamas arba bazė yra mažesnė už vieną, o rodiklis yra teigiamas.

Yra keturi atvejai, į kuriuos reikia atsižvelgti:

Apsiribosime pirmojo iš jų analize, o kitus skaitytojas svarstys pats.

Tegu tada lygybėje rodiklis negali būti nei neigiamas, nei lygus nuliui, todėl jis yra teigiamas, t. y. kaip reikia įrodyti.

3 pavyzdys. Sužinokite, kurie iš toliau pateiktų logaritmų yra teigiami, o kurie neigiami:

Sprendimas, a) kadangi skaičius 15 ir bazė 12 yra toje pačioje pusėje;

b) kadangi 1000 ir 2 yra vienoje įrenginio pusėje; šiuo atveju nėra svarbu, kad bazė būtų didesnė už logaritminį skaičių;

c) kadangi 3,1 ir 0,8 yra priešingose ​​vienybės pusėse;

G); Kodėl?

d) ; Kodėl?

Tokios savybės 4-6 dažnai vadinamos logaritmavimo taisyklėmis: jos leidžia, žinant kai kurių skaičių logaritmus, rasti kiekvieno jų sandaugos, koeficiento ir laipsnio logaritmus.

4 savybė (produkto logaritmo taisyklė). Kelių teigiamų skaičių sandaugos logaritmas tam tikroje bazėje yra lygus šių skaičių logaritmų sumai toje pačioje bazėje.

Įrodymas. Tegul pateikti skaičiai yra teigiami.

Jų sandaugos logaritmui rašome lygybę (26.1), kuri apibrėžia logaritmą:

Iš čia rasime

Palyginę pirmosios ir paskutinės išraiškos eksponentus, gauname reikiamą lygybę:

Atkreipkite dėmesį, kad sąlyga yra būtina; sandaugos iš dviejų logaritmas neigiami skaičiai prasminga, bet šiuo atveju gauname

Apskritai, jei kelių veiksnių sandauga yra teigiama, tada jo logaritmas yra lygus šių veiksnių absoliučių verčių logaritmų sumai.

5 savybė (datinių logaritmų ėmimo taisyklė). Teigiamų skaičių dalinio logaritmas yra lygus skirtumui tarp dividendo ir daliklio logaritmų, paimtų į tą pačią bazę. Įrodymas. Mes nuolat randame

Q.E.D.

Savybė 6 (laipsnio logaritmo taisyklė). Bet kurio teigiamo skaičiaus laipsnio logaritmas yra lygus to skaičiaus logaritmui, padaugintam iš eksponento.

Įrodymas. Dar kartą parašykime pagrindinę numerio tapatybę (26.1):

Q.E.D.

Pasekmė. Teigiamo skaičiaus šaknies logaritmas yra lygus radikalo logaritmui, padalytam iš šaknies eksponento:

Šios išvados pagrįstumą galima įrodyti įsivaizduojant, kaip ir naudojant 6 savybę.

4 pavyzdys. Paimkite logaritmą į a bazę:

a) (manoma, kad visos b, c, d, e reikšmės yra teigiamos);

b) (manoma, kad ).

Sprendimas, a) Šioje išraiškoje patogu pereiti prie trupmeninių laipsnių:

Remdamiesi lygybėmis (26.5)-(26.7), dabar galime rašyti:

Pastebime, kad su skaičių logaritmais atliekami paprastesni veiksmai, nei su pačiais skaičiais: dauginant skaičius jų logaritmai pridedami, dalinant – atimami ir t.t.

Štai kodėl skaičiavimo praktikoje naudojami logaritmai (žr. 29 pastraipą).

Atvirkštinis logaritmo veiksmas vadinamas potenciavimu, būtent: potencija yra veiksmas, kuriuo iš tam tikro skaičiaus logaritmo randamas pats skaičius. Iš esmės stiprinimas nėra joks ypatingas veiksmas: jis susijęs su bazės pakėlimu iki laipsnio (lygaus skaičiaus logaritmui). Terminas „potencijavimas“ gali būti laikomas termino „eksponentavimas“ sinonimu.

Potencuodami turite naudoti taisykles, atvirkštines logaritmavimo taisyklėms: logaritmų sumą pakeiskite sandaugos logaritmu, logaritmų skirtumą - koeficiento logaritmu ir tt Ypač jei priešais yra koeficientas logaritmo ženklo, tada potencijavimo metu jis turi būti perkeltas į eksponento laipsnius po logaritmo ženklu.

5 pavyzdys. Raskite N, jei žinoma, kad

Sprendimas. Atsižvelgiant į ką tik nurodytą potenciavimo taisyklę, koeficientus 2/3 ir 1/3, stovinčius prieš logaritmų ženklus dešinėje šios lygybės pusėje, perkelsime į eksponentus po šių logaritmų ženklais; mes gauname

Dabar logaritmų skirtumą pakeičiame koeficiento logaritmu:

kad gautume paskutinę trupmeną šioje lygybių grandinėje, išlaisvinome ankstesnę trupmeną nuo iracionalumo vardiklyje (25 punktas).

Savybė 7. Jei bazė yra didesnė už vieną, tada didesnis skaičius turi didesnį logaritmą (o mažesnis skaičius turi mažesnį), jei bazė yra mažesnė už vieną, tai didesnis skaičius turi mažesnį logaritmą (o mažesnis skaičius turi didesnį).

Ši savybė taip pat suformuluota kaip taisyklė imant nelygybių logaritmus, kurių abi pusės yra teigiamos:

Logarituojant nelygybes į bazę, didesnę už vienetą, nelygybės ženklas išsaugomas, o logarituojant iki bazės, mažesnės už vieną, nelygybės ženklas pasikeičia į priešingą (taip pat žr. 80 pastraipą).

Įrodymas paremtas 5 ir 3 savybėmis. Apsvarstykite atvejį, kai If , tada ir, imant logaritmus, gauname

(a ir N/M yra toje pačioje vienybės pusėje). Iš čia

Toliau pateikiamas a atvejis, skaitytojas tai išsiaiškins pats.

Logaritmas su baze a yra y funkcija (x) = log a x, atvirkštinė eksponentinė funkcija su baze a: x (y) = a y.

Dešimtainis logaritmas yra logaritmas iki skaičiaus pagrindo 10 : log x ≡ log 10 x.

Natūralus logaritmas yra logaritmas iki e pagrindo: ln x ≡ log e x.

2,718281828459045... ;
.

Logaritmo grafikas gaunamas iš eksponentinės funkcijos grafiko, atspindint jį tiesės y = x atžvilgiu. Kairėje yra funkcijos y grafikai (x) = log a x keturioms vertėms logaritmų bazės: a = 2 , a = 8 , a = 1/2 ir a = 1/8 . Diagrama rodo, kad kai a > 1 logaritmas didėja monotoniškai. Kai x didėja, augimas žymiai sulėtėja. At 0 < a < 1 logaritmas mažėja monotoniškai.

Logaritmo savybės

Domenas, vertybių rinkinys, didėjantis, mažėjantis

Logaritmas yra monotoninė funkcija, todėl ji neturi ekstremalių. Pagrindinės logaritmo savybės pateiktos lentelėje.

Domenas	0 < x < + ∞	0 < x < + ∞
Vertybių diapazonas	- ∞ < y < + ∞	- ∞ < y < + ∞
Monotoniškas	monotoniškai didėja	monotoniškai mažėja
Nuliai, y = 0	x = 1	x = 1
Sukirtimo taškai su ordinačių ašimi, x = 0	Nr	Nr
	+ ∞	- ∞
	- ∞	+ ∞

Privačios vertybės

Vadinamas logaritmas iki 10 bazės dešimtainis logaritmas ir žymimas taip:

Logaritmas iki pagrindo e paskambino natūralusis logaritmas:

Pagrindinės logaritmų formulės

Logaritmo savybės, kylančios iš atvirkštinės funkcijos apibrėžimo:

Pagrindinė logaritmų savybė ir jos pasekmės

Bazės pakeitimo formulė

Logaritmas yra matematinė logaritmo ėmimo operacija. Imant logaritmus faktorių sandaugai paverčiami terminų sumomis.

Potencija yra atvirkštinė matematinė logaritmo operacija. Potencijos metu tam tikra bazė pakeliama iki išraiškos laipsnio, per kurį atliekamas stiprinimas. Šiuo atveju terminų sumos paverčiamos veiksnių sandaugomis.

Pagrindinių logaritmų formulių įrodymas

Su logaritmais susijusios formulės kyla iš eksponentinių funkcijų formulių ir iš atvirkštinės funkcijos apibrėžimo.

Apsvarstykite eksponentinės funkcijos savybę
.
Tada
.
Taikykime eksponentinės funkcijos savybę
:
.

Įrodykime bazės pakeitimo formulę.
;
.
Darant prielaidą, kad c = b, turime:

Atvirkštinė funkcija

Logaritmo atvirkštinė bazė a yra eksponentinė funkcija su eksponentu a.

Jei tada

Jei tada

Logaritmo išvestinė

Modulio x logaritmo išvestinė:
.
N-osios eilės vedinys:
.
Išvedimo formulės >>>

Norint rasti logaritmo išvestinę, jis turi būti sumažintas iki pagrindo e.
;
.

Integralinis

Logaritmo integralas apskaičiuojamas integruojant dalimis: .
Taigi,

Išraiškos naudojant kompleksinius skaičius

Apsvarstykite kompleksinio skaičiaus funkciją z:
.
Išreikškime kompleksinį skaičių z per modulį r ir argumentas φ :
.
Tada, naudodamiesi logaritmo savybėmis, turime:
.
Arba

Tačiau argumentas φ nėra vienareikšmiškai apibrėžta. Jei įdėsite
, kur n yra sveikas skaičius,
tada jis bus tas pats skaičius skirtingiems n.

Todėl logaritmas, kaip sudėtingo kintamojo funkcija, nėra vienareikšmė funkcija.

Galios serijos išplėtimas

Kai plėtra vyksta:

Nuorodos:
I.N. Bronšteinas, K.A. Semendyaev, Matematikos vadovas inžinieriams ir kolegijų studentams, „Lan“, 2009 m.

Vienas iš primityvaus lygio algebros elementų yra logaritmas. Pavadinimas kilęs iš graikų kalba nuo žodžio „skaičius“ arba „galia“ ir reiškia laipsnį, iki kurio turi būti padidintas skaičius bazėje, norint rasti galutinį skaičių.

Logaritmų tipai

• log a b – skaičiaus b logaritmas bazei a (a > 0, a ≠ 1, b > 0);
• log b – dešimtainis logaritmas (logaritmas iki 10 bazės, a = 10);
• ln b – natūralusis logaritmas (logaritmas į bazę e, a = e).

Kaip išspręsti logaritmus?

B logaritmas iki a bazės yra eksponentas, kuriam b reikia pakelti į bazę a. Gautas rezultatas tariamas taip: „logaritmas nuo b iki bazės a“. Logaritminių uždavinių sprendimas yra tas, kad jums reikia nustatyti nurodytą galią skaičiais iš nurodytų skaičių. Yra keletas pagrindinių taisyklių, leidžiančių nustatyti ar išspręsti logaritmą, taip pat konvertuoti patį žymėjimą. Jais naudojant sprendžiamos logaritminės lygtys, randamos išvestinės, sprendžiami integralai, atliekama daug kitų operacijų. Iš esmės paties logaritmo sprendimas yra supaprastintas jo žymėjimas. Žemiau pateikiamos pagrindinės formulės ir savybės:

Bet kokiam a ; a > 0; a ≠ 1 ir bet kuriam x ; y > 0.

• a log a b = b – pagrindinė logaritminė tapatybė
• log a 1 = 0
• loga a = 1
• log a (x y) = log a x + log a y
• log a x/ y = log a x – log a y
• log a 1/x = -log a x
• log a x p = p log a x
• log a k x = 1/k log a x , kai k ≠ 0
• log a x = log a c x c
• log a x = log b x/ log b a – perėjimo į naują bazę formulė
• log a x = 1/log x a

Kaip išspręsti logaritmus - žingsnis po žingsnio sprendimo instrukcijos

• Pirmiausia užrašykite reikiamą lygtį.

Atkreipkite dėmesį: jei bazinis logaritmas yra 10, tada įrašas sutrumpinamas ir gaunamas dešimtainis logaritmas. Jei yra natūralusis skaičius e, tai jį užrašome, sumažindami iki natūralusis logaritmas. Tai reiškia, kad visų logaritmų rezultatas yra laipsnis, iki kurio pakeliamas bazinis skaičius, norint gauti skaičių b.

Tiesiogiai sprendimas slypi apskaičiuojant šį laipsnį. Prieš sprendžiant išraišką logaritmu, ją reikia supaprastinti pagal taisyklę, tai yra, naudojant formules. Pagrindines tapatybes galite rasti šiek tiek grįžę į straipsnį.

Logaritmų sudėjimas ir atėmimas dviem skirtingi skaičiai, bet su tais pačiais pagrindais, pakeiskite vienu logaritmu skaičių b ir c sandauga arba padalijimu atitinkamai. Tokiu atveju galite pritaikyti perkėlimo į kitą bazę formulę (žr. aukščiau).

Jei naudojate išraiškas logaritmui supaprastinti, reikia atsižvelgti į kai kuriuos apribojimus. Ir tai yra: logaritmo a bazė yra tik teigiamas skaičius, bet ne lygus vienetui. Skaičius b, kaip ir a, turi būti didesnis už nulį.

Pasitaiko atvejų, kai supaprastinus išraišką logaritmo skaičiais apskaičiuoti nepavyks. Pasitaiko, kad tokia išraiška neturi prasmės, nes daugelis galių yra neracionalūs skaičiai. Esant šiai sąlygai, palikite skaičiaus laipsnį kaip logaritmą.

Šiandien kalbėsime apie logaritmines formules ir pateiksime orientacinius sprendimų pavyzdžiai.

Jie patys reiškia sprendimų modelius pagal pagrindines logaritmų savybes. Prieš spręsdami taikydami logaritmines formules, priminsime visas savybes:

Dabar, remdamiesi šiomis formulėmis (ypatybėmis), parodysime logaritmų sprendimo pavyzdžiai.

Logaritmų sprendimo pagal formules pavyzdžiai.

Logaritmas teigiamas skaičius b bazei a (žymimas log a b) yra eksponentas, į kurį reikia pakelti a, kad gautume b, kai b > 0, a > 0 ir 1.

Pagal apibrėžimą log a b = x, kuris yra ekvivalentas a x = b, todėl log a a x = x.

Logaritmai, pavyzdžiai:

log 2 8 = 3, nes 2 3 = 8

log 7 49 = 2, nes 7 2 = 49

log 5 1/5 = -1, nes 5 -1 = 1/5

Dešimtainis logaritmas- tai paprastas logaritmas, kurio pagrindas yra 10. Jis žymimas kaip lg.

log 10 100 = 2, nes 10 2 = 100

Natūralus logaritmas- taip pat paprastasis logaritmas, logaritmas, bet su baze e (e = 2,71828... - neracionalus skaičius). Žymima kaip ln.

Patartina įsiminti logaritmų formules ar savybes, nes vėliau jų prireiks sprendžiant logaritmus, logaritmines lygtis ir nelygybes. Dar kartą panagrinėkime kiekvieną formulę su pavyzdžiais.

• Pagrindinė logaritminė tapatybė
  a log a b = b

  8 2log 8 3 = (8 2log 8 3) 2 = 3 2 = 9

• Produkto logaritmas lygus logaritmų sumai
  log a (bc) = log a b + log a c

  log 3 8,1 + log 3 10 = log 3 (8,1*10) = log 3 81 = 4

• Dalinio logaritmas lygus logaritmų skirtumui
  log a (b/c) = log a b - log a c

  9 log 5 50 /9 log 5 2 = 9 log 5 50- log 5 2 = 9 log 5 25 = 9 2 = 81

• Logaritminio skaičiaus laipsnio ir logaritmo pagrindo savybės

  Logaritminio skaičiaus eksponentas log a b m = mlog a b

  Logaritmo pagrindo eksponentas log a n b =1/n*log a b

  log a n b m = m/n*log a b,

  jei m = n, gauname log a n b n = log a b

  log 4 9 = log 2 2 3 2 = log 2 3

• Perėjimas prie naujo pagrindo
  log a b = log c b/log c a,

  jei c = b, gauname log b b = 1

  tada log a b = 1/log b a

  log 0,8 3*log 3 1,25 = log 0,8 3*log 0,8 1,25/log 0,8 3 = log 0,8 1,25 = log 4/5 5/4 = -1

Kaip matote, logaritmų formulės nėra tokios sudėtingos, kaip atrodo. Dabar, pažvelgę ​​į logaritmų sprendimo pavyzdžius, galime pereiti prie logaritminių lygčių. Išsamiau pažvelgsime į logaritminių lygčių sprendimo pavyzdžius straipsnyje: "". Nepraleisk!

Jei vis dar turite klausimų apie sprendimą, parašykite juos straipsnio komentaruose.

Pastaba: nusprendėme įgyti kitos klasės išsilavinimą ir studijuoti užsienyje.