Pasvirosios liestinės lygties radimo formulės. Internetinis skaičiuotuvas. Funkcijos grafiko tiesios liestinės tam tikrame taške lygtis

Straipsnyje išsamiai paaiškinamos išvestinės su apibrėžimai, geometrinė reikšmė grafiniai simboliai. Pavyzdžiais bus nagrinėjama liestinės linijos lygtis, rastos 2 eilės kreivių liestinės lygtys.

Yandex.RTB R-A-339285-1 1 apibrėžimas

Tiesės y = k x + b polinkio kampas vadinamas kampu α, kuris matuojamas nuo teigiamos x ašies krypties iki tiesės y = k x + b teigiama kryptimi.

Paveiksle x kryptis pažymėta žalia rodykle ir žalia lanku, o polinkio kampas – raudonu lanku. Mėlyna linija reiškia tiesią liniją.

2 apibrėžimas

Tiesės y = k x + b nuolydis vadinamas skaitiniu koeficientu k.

Kampinis koeficientas lygus tiesės liestinei, kitaip tariant k = t g α.

• Tiesės polinkio kampas lygus 0 tik tada, kai ji lygiagreti x, o nuolydis lygus nuliui, nes nulio liestinė lygi 0. Tai reiškia, kad lygties forma bus y = b.
• Jei tiesės y = k x + b pasvirimo kampas yra smailus, tada tenkinamos sąlygos 0< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0, o grafike yra padidėjimas.
• Jei α = π 2, tai tiesės vieta yra statmena x. Lygybė nurodoma x = c, kai reikšmė c yra tikrasis skaičius.
• Jei tiesės y = k x + b pasvirimo kampas yra bukas, tai jis atitinka sąlygas π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

3 apibrėžimas

Sekantas yra tiesė, einanti per 2 funkcijos f (x) taškus. Kitaip tariant, sekantas yra tiesi linija, nubrėžta per bet kuriuos du grafiko taškus suteikta funkcija.

Paveikslėlyje parodyta, kad A B yra sekantas, o f (x) yra juoda kreivė, α yra raudonas lankas, nurodantis sekanto pasvirimo kampą.

Kada nuolydis tiesė lygi polinkio kampo liestinei, aišku, kad stačiojo trikampio A B C liestinę galima rasti pagal priešingos kraštinės santykį su gretima.

4 apibrėžimas

Gauname formulę formos sekantui rasti:

k = t g α = B C A C = f (x B) - f x A x B - x A, kur taškų A ir B abscisės yra x A, x B ir f (x A), f (x) reikšmės B) yra reikšmių funkcijos šiuose taškuose.

Akivaizdu, kad sekanto kampinis koeficientas nustatomas naudojant lygybę k = f (x B) - f (x A) x B - x A arba k = f (x A) - f (x B) x A - x B , o lygtis turi būti parašyta taip y = f (x B) - f (x A) x B - x A x - x A + f (x A) arba
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .

Sekantas vizualiai padalija grafiką į 3 dalis: į kairę nuo taško A, nuo A iki B, į dešinę nuo B. Toliau pateiktame paveikslėlyje parodyta, kad yra trys sekantai, kurie laikomi sutampančiomis, tai yra, jie nustatomi naudojant panaši lygtis.

Pagal apibrėžimą aišku, kad tiesi linija ir jos sekantas tokiu atveju susilyginti.

Sekantas gali kelis kartus kirsti tam tikros funkcijos grafiką. Jei sekantei yra y = 0 formos lygtis, tai susikirtimo su sinusoidu taškų skaičius yra begalinis.

5 apibrėžimas

Funkcijos f (x) grafiko liestinė taške x 0 ; f (x 0) yra tiesė, einanti per nurodytą tašką x 0; f (x 0), kai yra segmentas, turintis daug x reikšmių, artimų x 0.

1 pavyzdys

Pažvelkime į toliau pateiktą pavyzdį atidžiau. Tada aišku, kad funkcija y = x + 1 apibrėžta tiesė laikoma liestine y = 2 x taške su koordinatėmis (1; 2). Siekiant aiškumo, reikia atsižvelgti į grafikus, kurių reikšmės yra artimos (1; 2). Funkcija y = 2 x rodoma juoda spalva, mėlyna linija yra liestinė, o raudonas taškas yra susikirtimo taškas.

Akivaizdu, kad y = 2 x susilieja su linija y = x + 1.

Norėdami nustatyti liestinę, turėtume atsižvelgti į liestinės A B elgesį, kai taškas B be galo artėja prie taško A. Aiškumo dėlei pateikiame brėžinį.

Sekantas A B, pažymėtas mėlyna linija, yra linkęs į pačios liestinės padėtį, o sekanto pasvirimo kampas α pradės linkti į pačios liestinės polinkio kampą α x.

6 apibrėžimas

Funkcijos y = f (x) grafiko liestinė taške A laikoma sekanto A B ribine padėtimi, nes B linksta į A, tai yra, B → A.

Dabar pereikime prie funkcijos išvestinės taške geometrinės reikšmės.

Pereikime prie funkcijos f (x) sekanto A B, kur A ir B su koordinatėmis x 0, f (x 0) ir x 0 + ∆ x, f (x 0 + ∆ x) ir ∆ x yra žymimas kaip argumento padidėjimas . Dabar funkcija įgaus formą ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . Aiškumo dėlei pateiksime piešinio pavyzdį.

Apsvarstykite gautą statųjį trikampį A B C. Spręsdami naudojame liestinės apibrėžimą, tai yra, gauname ryšį ∆ y ∆ x = t g α . Iš liestinės apibrėžimo išplaukia, kad lim ∆ x → 0 ∆ y ∆ x = t g α x . Pagal išvestinės taške taisyklę gauname, kad išvestinė f (x) taške x 0 vadinama funkcijos didėjimo ir argumento prieaugio santykio riba, kur ∆ x → 0 , tada pažymime kaip f (x 0) = lim ∆ x → 0 ∆ y ∆ x .

Iš to seka, kad f " (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, kur k x žymimas liestinės nuolydžiu.

Tai yra, mes nustatome, kad f ' (x) gali egzistuoti taške x 0 ir kaip nurodytos funkcijos grafiko liestinė taške, lygiame x 0, f 0 (x 0), kur liestinės nuolydis taške lygus išvestinei taške x 0 . Tada gauname, kad k x = f " (x 0) .

Geometrinė reikšmė funkcijos išvestinė taške yra ta, kad pateikiama grafiko liestinės egzistavimo tame pačiame taške samprata.

Norint parašyti bet kurios tiesės lygtį plokštumoje, būtina turėti kampo koeficientą su tašku, per kurį ji eina. Jo žymėjimas sankryžoje laikomas x 0.

Funkcijos y = f (x) grafiko liestinės lygtis taške x 0, f 0 (x 0) yra y = f "(x 0) x - x 0 + f (x 0).

Tai reiškia, kad galutinė išvestinės f "(x 0) reikšmė gali nustatyti liestinės padėtį, tai yra vertikaliai, jei lim x → x 0 + 0 f "(x) = ∞ ir lim x → x 0 - 0 f "(x ) = ∞ arba visai nebuvimas su sąlyga lim x → x 0 + 0 f " (x) ≠ lim x → x 0 - 0 f " (x) .

Liestinės vieta priklauso nuo jos kampinio koeficiento k x = f "(x 0) reikšmės. Kai lygiagreti o x ašiai, gauname, kad k k = 0, kai lygiagreti o y - k x = ∞, ir formos liestinės lygtis x = x 0 didėja, kai k x > 0, mažėja kaip k x< 0 .

2 pavyzdys

Sudarykite funkcijos y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 grafiko liestinės lygtį taške su koordinatėmis (1; 3) ir nustatykite pasvirimo kampą.

Sprendimas

Pagal sąlygą turime, kad funkcija apibrėžta visiems realūs skaičiai. Nustatome, kad taškas su koordinatėmis, nurodytomis sąlyga (1; 3), yra liesties taškas, tada x 0 = - 1, f (x 0) = - 3.

Būtina rasti išvestinę taške, kurio reikšmė - 1. Mes tai gauname

y " = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = e x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = e x + 1 + x 2 - 6 - 3 3 y " (x 0) = y " (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3

F' (x) reikšmė liestinės taške yra liestinės nuolydis, lygus nuolydžio liestine.

Tada k x = t g α x = y " (x 0) = 3 3

Iš to seka, kad α x = a r c t g 3 3 = π 6

Atsakymas: liestinės lygtis įgauna formą

y = f " (x 0) x - x 0 + f (x 0) y = 3 3 (x + 1) - 3 y = 3 3 x - 9 - 3 3

Aiškumo dėlei pateikiame pavyzdį grafinėje iliustracijoje.

Pradinės funkcijos grafikui naudojama juoda spalva, Mėlyna spalva– liestinės vaizdas, raudonas taškas – lietimo taškas. Paveikslėlis dešinėje rodo padidintą vaizdą.

3 pavyzdys

Nustatykite, ar yra duotosios funkcijos grafiko liestinė
y = 3 · x - 1 5 + 1 taške su koordinatėmis (1 ; 1) . Parašykite lygtį ir nustatykite pasvirimo kampą.

Sprendimas

Pagal sąlygą turime, kad tam tikros funkcijos apibrėžimo sritis yra visų realiųjų skaičių aibė.

Pereikime prie išvestinės paieškos

y " = 3 x - 1 5 + 1 " = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5

Jei x 0 = 1, tai f' (x) neapibrėžtas, bet ribos rašomos kaip lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 · 1 + 0 = + ∞ ir lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , o tai reiškia taške (1; 1) yra vertikali liestinė.

Atsakymas: lygtis bus x = 1, kur pasvirimo kampas bus lygus π 2.

Kad būtų aiškumo, pavaizduokime jį grafiškai.

4 pavyzdys

Raskite funkcijos y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2 grafiko taškus, kur

1. Nėra liestinės;
2. Liestinė lygiagreti x;
3. Liestinė lygiagreti tiesei y = 8 5 x + 4.

Sprendimas

Būtina atkreipti dėmesį į apibrėžimo apimtį. Pagal sąlygą turime, kad funkcija apibrėžta visų realiųjų skaičių aibėje. Išplečiame modulį ir sprendžiame sistemą intervalais x ∈ - ∞ ; 2 ir [-2; + ∞) . Mes tai gauname

y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; + ∞)

Būtina atskirti funkciją. Mes tai turime

y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 ", x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35), x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; + ∞)

Kai x = − 2, tada išvestinė neegzistuoja, nes tame taške vienpusės ribos nėra lygios:

lim x → - 2 - 0 y " (x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y " (x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

Apskaičiuojame funkcijos reikšmę taške x = - 2, kur tai gauname

1. y (- 2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2, tai yra, liestinė taške ( - 2; - 2) nebus.
2. Liestinė yra lygiagreti x, kai nuolydis lygus nuliui. Tada k x = t g α x = f "(x 0). Tai yra, reikia rasti tokio x reikšmes, kai funkcijos išvestinė paverčia ją nuliu. Tai yra f ' reikšmės. (x) bus lietimo taškai, kur liestinė lygiagreti x .

Kai x ∈ - ∞ ; - 2, tada - 1 5 (x 2 + 12 x + 35) = 0, o x ∈ (- 2; + ∞) gauname 1 5 (x 2 - 4 x + 3) = 0.

1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = -12 + 4 2 = -5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞

Apskaičiuokite atitinkamas funkcijų reikšmes

y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3

Vadinasi - 5; 8 5, - 4; 4 3, 1; 8 5, 3; 4 3 laikomi reikiamais funkcijos grafiko taškais.

Pažiūrėkime į grafinį sprendimo vaizdą.

Juoda linija yra funkcijos grafikas, raudoni taškai yra lietimo taškai.

1. Kai tiesės lygiagrečios, kampiniai koeficientai yra lygūs. Tada funkcijos grafike reikia ieškoti taškų, kuriuose nuolydis bus lygus reikšmei 8 5. Norėdami tai padaryti, turite išspręsti y formos lygtį "(x) = 8 5. Tada, jei x ∈ - ∞; - 2, gauname, kad - 1 5 (x 2 + 12 x + 35) = 8 5, o jei x ∈ ( - 2 ; + ∞), tai 1 5 (x 2 - 4 x + 3) = 8 5.

Pirmoji lygtis neturi šaknų, nes diskriminantas yra mažesnis už nulį. Užsirašykime tai

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0

Kita lygtis turi dvi realias šaknis

1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞

Pereikime prie funkcijos reikšmių paieškos. Mes tai gauname

y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3

Taškai su reikšmėmis - 1; 4 15, 5; 8 3 yra taškai, kuriuose liestinės yra lygiagrečios tiesei y = 8 5 x + 4.

Atsakymas: juoda linija – funkcijos grafikas, raudona linija – y = 8 grafikas 5 x + 4, mėlyna linija – liestinės taškuose - 1; 4 15, 5; 8 3.

Tam tikroms funkcijoms gali būti begalinis liestinių skaičius.

5 pavyzdys

Parašykite visų galimų funkcijos y = 3 cos 3 2 x - π 4 - 1 3 liestinių lygtis, kurios yra statmenos tiesei y = - 2 x + 1 2.

Sprendimas

Norint sudaryti liestinės lygtį, reikia rasti liestinės taško koeficientą ir koordinates, remiantis tiesių statmenumo sąlyga. Apibrėžimas yra toks: kampinių koeficientų, kurie yra statmeni tiesėms, sandauga yra lygi - 1, tai yra, parašyta kaip k x · k ⊥ = - 1. Iš sąlygos gauname, kad kampinis koeficientas yra statmenai tiesei ir yra lygus k ⊥ = - 2, tada k x = - 1 k ⊥ = - 1 - 2 = 1 2.

Dabar reikia rasti kontaktinių taškų koordinates. Turite rasti x ir tada jo reikšmę duotai funkcijai. Atkreipkite dėmesį, kad iš geometrinės išvestinės reikšmės taške
x 0 gauname, kad k x = y "(x 0). Iš šios lygybės randame sąlyčio taškų x reikšmes.

Mes tai gauname

y " (x 0) = 3 cos 3 2 x 0 - π 4 - 1 3 " = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 = - 9 2 sin 3 2 x 0 - π 4 ⇒ k x = y " (x 0) ⇔ - 9 2 sin 3 2 x 0 - π 4 = 1 2 ⇒ sin 3 2 x 0 - π 4 = - 1 9

Ši trigonometrinė lygtis bus naudojama liestinių taškų ordinatėms apskaičiuoti.

3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk arba 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk

3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk arba 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 - arc sin 1 9 + 2 πk arba x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z yra sveikųjų skaičių aibė.

rasta x sąlyčio taškų. Dabar reikia pereiti prie y reikšmių paieškos:

y 0 = 3 cos 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - sin 2 3 2 x 0 - π 4 - 1 3 arba y 0 = 3 - 1 - sin 2 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - - 1 9 2 - 1 3 arba y 0 = 3 - 1 - - 1 9 2 - 1 3

y 0 = 4 5 - 1 3 arba y 0 = - 4 5 + 1 3

Iš to gauname, kad 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; - 4 5 + 1 3 yra lietimo taškai.

Atsakymas: reikalingos lygtys bus parašytos kaip

y = 1 2 x - 2 3 π 4 - arc sin 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + arc sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z

Norėdami vizualiai pavaizduoti, apsvarstykite funkciją ir liestinę koordinačių tiesėje.

Paveikslėlyje parodyta, kad funkcija yra intervale [-10; 10 ], kur juoda linija yra funkcijos grafikas, mėlynos linijos yra liestinės, kurios yra statmenos duotai y = - 2 x + 1 2 formos linijai. Raudoni taškai yra prisilietimo taškai.

2 eilės kreivių kanoninės lygtys nėra vienareikšmės funkcijos. Jų liestinės lygtys sudaromos pagal žinomas schemas.

Apskritimo liestinė

Apibrėžti apskritimą, kurio centras yra taške x c ​​e n t e r ; y c e n t e r ir spindulį R, taikykite formulę x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 .

Šią lygybę galima parašyti kaip dviejų funkcijų sąjungą:

y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r

Pirmoji funkcija yra viršuje, o antroji – apačioje, kaip parodyta paveikslėlyje.

Sudaryti apskritimo lygtį taške x 0; y 0 , kuris yra viršutiniame arba apatiniame puslankiu, turėtumėte rasti y = R 2 - x - x c e n t e r 2 + y c e n t e r arba y = - R 2 - x - x c e n t e r 2 + formos funkcijos grafiko lygtį. y c e n t e r nurodytame taške.

Kai taškuose x c ​​e n t e r ; y c e n t e r + R ir x c e n t e r ; y c e n t e r - R liestinės gali būti pateiktos lygtimis y = y c e n t e r + R ir y = y c e n t e r - R , o taškuose x c ​​e n t e r + R ; y c e n t e r ir
x c e n t e r - R ; y c e n t e r bus lygiagreti o y, tada gauname x = x c e n t e r + R ir x = x c e n t e r - R formos lygtis.

Elipsės liestinė

Kai elipsė turi centrą x c e n t e r ; y c e n t e r su pusiau ašimis a ir b, tada ją galima nurodyti naudojant lygtį x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1.

Elipsė ir apskritimas gali būti žymimi sujungiant dvi funkcijas, būtent viršutinę ir apatinę puselipsę. Tada mes tai gauname

y = b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r

Jei liestinės yra elipsės viršūnėse, tada jos yra lygiagrečios apie x arba apie y. Žemiau, kad būtų aiškumo, apsvarstykite paveikslą.

6 pavyzdys

Parašykite elipsės liestinės x - 3 2 4 + y - 5 2 25 = 1 lygtį taškuose, kurių x reikšmės yra lygios x = 2.

Sprendimas

Būtina rasti liestinės taškus, atitinkančius reikšmę x = 2. Mes pakeičiame esamą elipsės lygtį ir randame

x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5

Tada 2; 5 3 2 + 5 ir 2; - 5 3 2 + 5 yra liestinės taškai, priklausantys viršutinei ir apatinei puselipsei.

Pereikime prie elipsės lygties y atžvilgiu radimo ir sprendimo. Mes tai gauname

x - 3 2 4 + y - 5 2 25 = 1 m - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2

Akivaizdu, kad viršutinė puselipsė nurodoma naudojant y = 5 + 5 2 4 - x - 3 2 formos funkciją, o apatinė puselipsė y = 5 - 5 2 4 - x - 3 2.

Taikykime standartinį algoritmą, kad sukurtume funkcijos grafiko liestinės taške lygtį. Parašykime, kad pirmosios liestinės lygtis taške 2; 5 3 2 + 5 atrodys taip

y " = 5 + 5 2 4 - x - 3 2 " = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y " (x 0) = y " (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5

Mes nustatome, kad antrosios liestinės su reikšme taške lygtis
2 ; - 5 3 2 + 5 įgauna formą

y " = 5 - 5 2 4 - (x - 3) 2 " = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y " (x 0) = y " (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5

Grafiškai liestinės žymimos taip:

Hiperbolės liestinė

Kai hiperbolė turi centrą x c e n t e r ; y c e n t e r ir viršūnės x c e n t e r + α ; y c e n t e r ir x c e n t e r - α ; y c e n t e r , vyksta nelygybė x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1, jei su viršūnėmis x c e n t e r ; y c e n t e r + b ir x c e n t e r ; y c e n t e r - b , tada nurodoma naudojant nelygybę x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

Hiperbolė gali būti pavaizduota kaip dvi kombinuotos formos funkcijos

y = b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r arba y = b a · (x - t + t e r y) = - b a · (x - x c e n t e r) 2 + a 2 + y c e n t e r

Pirmuoju atveju liestinės yra lygiagrečios y, o antruoju - x.

Iš to seka, kad norint rasti hiperbolės liestinės lygtį, reikia išsiaiškinti, kuriai funkcijai priklauso liesties taškas. Norint tai nustatyti, būtina pakeisti lygtis ir patikrinti tapatybę.

7 pavyzdys

Parašykite lygtį hiperbolės liestinės x - 3 2 4 - y + 3 2 9 = 1 taške 7; - 3 3 - 3 .

Sprendimas

Norint rasti hiperbolę, reikia transformuoti sprendimo įrašą naudojant 2 funkcijas. Mes tai gauname

x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 ir y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3

Būtina nustatyti, kuriai funkcijai priklauso duotas taškas su koordinatėmis 7; - 3 3 - 3 .

Akivaizdu, kad norint patikrinti pirmąją funkciją, reikia y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3, tada taškas nepriklauso grafikui, nes lygybė negalioja.

Antrajai funkcijai turime, kad y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3, tai reiškia, kad taškas priklauso duotam grafikui. Iš čia turėtumėte rasti šlaitą.

Mes tai gauname

y " = - 3 2 (x - 3) 2 - 4 - 3 " = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y " (x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3

Atsakymas: liestinės lygtis gali būti pavaizduota kaip

y = – 3 x – 7 – 3 3 – 3 = – 3 x + 4 3 – 3

Tai aiškiai pavaizduota taip:

Parabolės liestinė

Norėdami sukurti parabolės y = a x 2 + b x + c liestinės lygtį taške x 0, y (x 0), turite naudoti standartinį algoritmą, tada lygtis bus y = y "(x) 0) x - x 0 + y ( x 0).Tokia liestinė viršūnėje lygiagreti x.

Turėtumėte apibrėžti parabolę x = a y 2 + b y + c kaip dviejų funkcijų sąjungą. Todėl turime išspręsti y lygtį. Mes tai gauname

x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a

Grafiškai pavaizduota taip:

Norėdami sužinoti, ar taškas x 0, y (x 0) priklauso funkcijai, švelniai elkitės pagal standartinį algoritmą. Tokia liestinė bus lygiagreti o y parabolės atžvilgiu.

8 pavyzdys

Parašykite grafiko x - 2 y 2 - 5 y + 3 liestinės lygtį, kai liestinės kampas yra 150 °.

Sprendimas

Sprendimą pradedame pavaizduodami parabolę kaip dvi funkcijas. Mes tai gauname

2 m. 2 - 5 m + 3 - x = 0 D = (- 5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4

Nuolydžio reikšmė lygi išvestinės reikšmei šios funkcijos taške x 0 ir lygi pasvirimo kampo tangentei.

Mes gauname:

k x = y "(x 0) = t g α x = t g 150 ° = - 1 3

Iš čia nustatome sąlyčio taškų x reikšmę.

Pirmoji funkcija bus parašyta kaip

y " = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3

Akivaizdu, kad tikrų šaknų nėra, nes gavome neigiamą reikšmę. Darome išvadą, kad tokiai funkcijai nėra liestinės su 150° kampu.

Antroji funkcija bus parašyta kaip

y " = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4

Turime, kad sąlyčio taškai yra 23 4 ; - 5 + 3 4 .

Atsakymas: liestinės lygtis įgauna formą

y = - 1 3 x - 23 4 + - 5 + 3 4

Pavaizduokime jį grafiškai taip:

Jei tekste pastebėjote klaidą, pažymėkite ją ir paspauskite Ctrl+Enter

Y = f(x) ir jei šioje vietoje į funkcijos grafiką galima nubrėžti liestinę, kuri nėra statmena abscisių ašiai, tai liestinės kampinis koeficientas lygus f"(a). Pavyzdžiui, § 33 buvo nustatyta, kad funkcijos y = sin x (sinusoidės) grafikas pradžioje sudaro 45° kampą su x ašimi (tiksliau, liestinės grafikas pradžioje sudaro 45° kampą su teigiama x ašies kryptimi), o 5 pavyzdyje pagal pateiktą grafiką buvo rasti 33 taškai funkcijas, kurioje liestinė lygiagreti x ašiai. 33 straipsnio 2 pavyzdyje buvo sudaryta funkcijos y = x 2 grafiko liestinės lygtis taške x = 1 (tiksliau, taške (1; 1), bet dažniau yra tik abscisės reikšmė nurodyta, manydama, kad jei žinoma abscisių reikšmė, tai ordinatės reikšmę galima rasti iš lygties y = f(x)). Šiame skyriuje mes sukursime bet kurios funkcijos grafiko liestinės lygties sudarymo algoritmą.

Tegul funkcija y = f(x) ir taškas M (a; f(a)) yra duotas, taip pat žinoma, kad f"(a) egzistuoja. Sukurkime lygtį grafiko liestinei. suteikta funkcija duotas taškas. Ši lygtis, kaip ir bet kurios tiesės, kuri nėra lygiagreti ordinačių ašiai, lygtis turi formą y = kx+m, todėl užduotis yra rasti koeficientų k ir m reikšmes.

Su kampiniu koeficientu k problemų nėra: žinome, kad k = f "(a). Norėdami apskaičiuoti m reikšmę, naudojame tai, kad norima tiesė eina per tašką M(a; f (a)) Tai reiškia, kad jei koordinačių tašką M pakeičiame tiesės lygtimi, gauname teisingą lygybę: f(a) = ka+m, iš kurios gauname, kad m = f(a) - ka.
Belieka pakeisti nustatytas rinkinio koeficientų vertes lygtis tiesiai:

Gavome funkcijos y = f(x) grafiko liestinės taške x=a lygtį.
Jei, tarkim,
Rastas reikšmes a = 1, f(a) = 1 f"(a) = 2 pakeitę į (1) lygtį, gauname: y = 1+2(x-f), ty y = 2x-1.
Palyginkite šį rezultatą su gautu 2 pavyzdyje iš § 33. Žinoma, nutiko tas pats.
Sukurkime funkcijos y = tan x grafiko liestinės lygtį pradinėje vietoje. Mes turime: tai reiškia cos x f"(0) = 1. Rastas reikšmes a = 0, f(a) = 0, f"(a) = 1 pakeisdami į (1) lygtį, gauname: y = x.
Štai kodėl nubrėžėme tangentoidą § 15 (žr. 62 pav.) per koordinačių pradžią 45° kampu abscisių ašies atžvilgiu.
Išspręskite šiuos pakankamai paprasti pavyzdžiai, mes iš tikrųjų naudojome tam tikrą algoritmą, kuris yra (1) formulėje. Padarykime šį algoritmą aiškų.

FUNKCIJOS y = f(x) GRAFIKOS LIETTINĖS LYGTYBĖS ALGORITMAS SUDARYTI

1) Pažymėkite liestinės taško abscisę raide a.
2) Apskaičiuokite 1 (a).
3) Raskite f"(x) ir apskaičiuokite f"(a).
4) Rastus skaičius a, f(a), (a) pakeiskite į (1) formulę.

1 pavyzdys. Parašykite funkcijos grafiko liestinės lygtį taške x = 1.
Naudokime algoritmą, atsižvelgdami į tai šiame pavyzdyje

Fig. 126 pavaizduota hiperbolė, nutiesta tiesė y = 2.
Brėžinys patvirtina minėtus skaičiavimus: iš tiesų, linija y = 2 paliečia hiperbolę taške (1; 1).

Atsakymas: y = 2- x.
2 pavyzdys. Nubrėžkite funkcijos grafiko liestinę, kad ji būtų lygiagreti tiesei y = 4x - 5.
Paaiškinkime problemos formuluotę. Reikalavimas „nubrėžti liestinę“ paprastai reiškia „sudaryti liestinės lygtį“. Tai logiška, nes jei žmogus sugebėjo sukurti liestinės lygtį, vargu ar jam kils sunkumų sukonstruodamas tiesę koordinačių plokštumoje, naudodamas jos lygtį.
Naudokime tangentinės lygties sudarymo algoritmą, atsižvelgdami į tai, kad šiame pavyzdyje Tačiau, skirtingai nei ankstesniame pavyzdyje, yra dviprasmiškumo: liestinės taško abscisė nėra aiškiai nurodyta.
Pradėkime taip galvoti. Norima liestinė turi būti lygiagreti tiesei y = 4x-5. Dvi tiesės yra lygiagrečios tada ir tik tada, kai jų nuolydžiai yra vienodi. Tai reiškia, kad liestinės kampinis koeficientas turi būti lygus nurodytos tiesės kampiniam koeficientui: Taigi a reikšmę galime rasti iš lygties f"(a) = 4.
Mes turime:
Iš lygties Tai reiškia, kad yra dvi liestinės, kurios tenkina uždavinio sąlygas: viena taške su abscise 2, kita taške su abscise -2.
Dabar galite sekti algoritmą.

3 pavyzdys. Iš taško (0; 1) nubrėžkite funkcijos grafiko liestinę
Panaudokime tangentinės lygties sudarymo algoritmą, atsižvelgdami į tai, kad šiame pavyzdyje Atkreipkite dėmesį, kad čia, kaip ir 2 pavyzdyje, liestinės taško abscisė nėra aiškiai nurodyta. Nepaisant to, mes laikomės algoritmo.

Pagal sąlygą liestinė eina per tašką (0; 1). Pakeitę reikšmes x = 0, y = 1 į (2) lygtį, gauname:
Kaip matote, šiame pavyzdyje tik ketvirtame algoritmo žingsnyje pavyko rasti liestinės taško abscisę. Pakeitę reikšmę a =4 į (2) lygtį, gauname:

Fig. 127 pateikta nagrinėjamo pavyzdžio geometrinė iliustracija: nubraižytas funkcijos grafikas

32 straipsnyje pažymėjome, kad funkcijai y = f(x), turinčiai išvestinę fiksuotame taške x, galioja apytikslė lygybė:

Tolesnio samprotavimo patogumui pakeiskime žymėjimą: vietoj x rašysime a, vietoj x ir atitinkamai vietoj x-a. Tada aukščiau parašyta apytikslė lygybė bus tokia:

Dabar pažiūrėkite į pav. 128. Funkcijos y = f(x) grafiko taške M (a; f (a)) nubrėžta liestinė. Taškas x pažymėtas x ašyje arti a. Aišku, kad f(x) yra funkcijos grafiko ordinatė nurodytame taške x. Kas yra f(a) + f"(a) (x-a)? Tai tą patį tašką x atitinkančios liestinės ordinatė – žr. (1) formulę. Ką reiškia apytikslė lygybė (3)? Faktas kad Norėdami apskaičiuoti apytikslę funkcijos reikšmę, paimkite liestinės ordinačių reikšmę.

4 pavyzdys. Raskite apytikslę vertę skaitinė išraiška 1,02 7 .
Tai apie apie funkcijos y = x 7 reikšmės radimą taške x = 1.02. Naudokime formulę (3), atsižvelgdami į tai šiame pavyzdyje
Rezultate gauname:

Jei naudosime skaičiuotuvą, gausime: 1,02 7 = 1,148685667...
Kaip matote, apytikslis tikslumas yra gana priimtinas.
Atsakymas: 1,02 7 =1,14.

A.G. Mordkovičiaus algebra 10 klasė

Kalendorinis teminis planavimas matematikoje, vaizdo įrašą matematika internete, matematika mokykloje parsisiųsti

Pamokos turinys pamokų užrašai remiančios kadrinės pamokos pristatymo pagreitinimo metodus interaktyvios technologijos Praktika užduotys ir pratimai savikontrolės seminarai, mokymai, atvejai, užduotys namų darbai diskusija klausimai retoriniai mokinių klausimai Iliustracijos garso, vaizdo klipai ir multimedija nuotraukos, paveikslėliai, grafika, lentelės, diagramos, humoras, anekdotai, anekdotai, komiksai, palyginimai, posakiai, kryžiažodžiai, citatos Priedai tezės straipsniai gudrybės smalsiems lopšiai vadovėliai pagrindinis ir papildomas terminų žodynas kita Vadovėlių ir pamokų tobulinimasklaidų taisymas vadovėlyje vadovėlio fragmento atnaujinimas, naujovių elementai pamokoje, pasenusių žinių keitimas naujomis Tik mokytojams tobulos pamokos kalendorinis planas metams Gairės diskusijų programos Integruotos pamokos

Funkcijos grafiko liestinės lygtis

P. Romanovas, T. Romanova,
Magnitogorskas,
Čeliabinsko sritis

Funkcijos grafiko liestinės lygtis

Straipsnis publikuotas remiant ITAKA+ viešbučių kompleksui. Apsistoję laivų statytojų mieste Severodvinske nesusidursite su laikino būsto paieškos problema. , viešbučių komplekso „ITHAKA+“ svetainėje http://itakaplus.ru galite lengvai ir greitai išsinuomoti butą mieste bet kokiam laikotarpiui, mokėdami kasdien.

Įjungta moderni scena ugdymo ugdymas, vienas pagrindinių jo uždavinių – kūrybiškai mąstančios asmenybės formavimas. Mokinių kūrybiškumas gali būti ugdomas tik sistemingai įtraukiant į tiriamosios veiklos pagrindus. Pagrindas mokiniams panaudoti savo kūrybines galias, gebėjimus ir talentus – visavertės žinios ir gebėjimai. Šiuo atžvilgiu nemažą reikšmę turi pagrindinių žinių ir įgūdžių sistemos formavimo kiekvienai mokyklinio matematikos kurso temai problema. Tuo pačiu metu visaverčiai įgūdžiai turėtų būti didaktinis ne atskirų užduočių, o kruopščiai apgalvotos jų sistemos tikslas. Plačiąja prasme sistema suprantama kaip visuma tarpusavyje susijusių sąveikaujančių elementų, kurie turi vientisumą ir stabilią struktūrą.

Panagrinėkime metodą, kaip mokyti studentus, kaip parašyti funkcijos grafiko liestinės lygtį. Iš esmės visos liestinės lygties radimo problemos kyla dėl būtinybės iš eilučių rinkinio (ryšulio, šeimos) pasirinkti tas, kurios tenkina tam tikrą reikalavimą – jos yra liestinės su tam tikros funkcijos grafiku. Šiuo atveju eilučių rinkinį, iš kurio atliekamas pasirinkimas, galima nurodyti dviem būdais:

a) taškas, esantis xOy plokštumoje (centrinis linijų pieštukas);
b) kampo koeficientas (lygiagretusis tiesių pluoštas).

Šiuo atžvilgiu, tirdami temą „Funkcijos grafiko liestinė“, siekdami išskirti sistemos elementus, nustatėme dviejų tipų problemas:

1) liestinės, pateiktos taško, per kurį ji eina, uždaviniai;
2) jos nuolydžio pateiktos liestinės uždaviniai.

Tangentinių uždavinių sprendimo mokymai buvo vykdomi naudojant A.G. pasiūlytą algoritmą. Mordkovičius. Jo esminis skirtumas iš jau žinomų yra tai, kad liestinės taško abscisė žymima raide a (vietoj x0), todėl liestinės lygtis įgauna formą

y = f(a) + f "(a)(x – a)

(palyginkite su y = f(x 0) + f "(x 0)(x – x 0)). Ši metodinė technika, mūsų nuomone, leidžia studentams greitai ir lengvai suprasti, kur parašytos esamo taško koordinatės. bendroji liestinės lygtis ir kur yra sąlyčio taškai.

Funkcijos y = f(x) grafiko liestinės lygties sudarymo algoritmas

1. Pažymėkite liestinės taško abscisę raide a.
2. Raskite f(a).
3. Raskite f "(x) ir f "(a).
4. Pakeiskite rastus skaičius a, f(a), f "(a) į bendrąją liestinės lygtį y = f(a) = f "(a)(x – a).

Šis algoritmas gali būti sudarytas remiantis studentų savarankišku operacijų identifikavimu ir jų įgyvendinimo seka.

Praktika parodė, kad nuoseklus kiekvienos pagrindinės problemos sprendimas naudojant algoritmą leidžia lavinti funkcijos grafiko liestinės lygties rašymo etapais įgūdžius, o algoritmo žingsniai yra veiksmų atskaitos taškai. . Šis požiūris atitinka laipsniško psichinių veiksmų formavimo teoriją, kurią sukūrė P.Ya. Galperinas ir N.F. Talyzina.

Pirmojo tipo užduotyse buvo nustatytos dvi pagrindinės užduotys:

• liestinė eina per tašką, esantį kreivėje (1 uždavinys);
• liestinė eina per tašką, esantį ne ant kreivės (2 uždavinys).

Užduotis 1. Parašykite funkcijos grafiko liestinės lygtį taške M(3; – 2).

Sprendimas. Taškas M(3; – 2) yra liestinės taškas, nes

1. a = 3 – liestinės taško abscisė.
2. f(3) = – 2.
3. f "(x) = x 2 – 4, f "(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – liestinės lygtis.

2 uždavinys. Užrašykite funkcijos y = – x 2 – 4x + 2, einančios per tašką M(– 3; 6), grafiko visų liestinių lygtis.

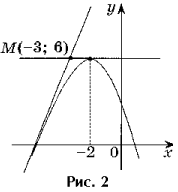Sprendimas. Taškas M(– 3; 6) nėra liestinės taškas, nes f(– 3) 6 (2 pav.).

2. f(a) = – a 2 – 4a + 2.
3. f "(x) = – 2x – 4, f "(a) = – 2a – 4.
4. y = – a 2 – 4a + 2 – 2(a + 2)(x – a) – liestinės lygtis.

Liestinė eina per tašką M(– 3; 6), todėl jos koordinatės tenkina liestinės lygtį.

6 = – a 2 – 4a + 2 – 2(a + 2) (– 3 – a),
a 2 + 6a + 8 = 0^ a 1 = – 4, a 2 = – 2.

Jei a = – 4, tada liestinės lygtis yra y = 4x + 18.

Jei a = – 2, tai liestinės lygtis yra y = 6.

Antrojo tipo pagrindinės užduotys bus šios:

• liestinė lygiagreti kokiai nors tiesei (3 uždavinys);
• liestinė eina tam tikru kampu į duotąją tiesę (4 uždavinys).

3 uždavinys. Užrašykite visų funkcijos y = x 3 – 3x 2 + 3, lygiagrečios tiesei y = 9x + 1, grafiko liestinių lygtis.

Sprendimas.

1. a – liestinės taško abscisė.
2. f(a) = a 3 – 3a 2 + 3.
3. f "(x) = 3x 2 – 6x, f "(a) = 3a 2 - 6a.

Bet, kita vertus, f "(a) = 9 (lygiagretumo sąlyga). Tai reiškia, kad turime išspręsti lygtį 3a 2 – 6a = 9. Jos šaknys yra a = – 1, a = 3 (3 pav.). ).

4. 1) a = – 1;
2) f(– 1) = – 1;
3) f "(– 1) = 9;
4) y = – 1 + 9(x + 1);

y = 9x + 8 – liestinės lygtis;

1) a = 3;
2) f(3) = 3;
3) f "(3) = 9;
4) y = 3 + 9 (x – 3);

y = 9x – 24 – liestinės lygtis.

4 uždavinys. Užrašykite funkcijos y = 0,5x 2 – 3x + 1, 45° kampu einančios į tiesę y = 0, grafiko liestinės lygtį (4 pav.).

Sprendimas. Iš sąlygos f "(a) = tan 45° randame a: a – 3 = 1^a = 4.

1. a = 4 – liestinės taško abscisė.
2. f(4) = 8 – 12 + 1 = – 3.
3. f "(4) = 4 – 3 = 1.
4. y = – 3 + 1(x – 4).

y = x – 7 – liestinės lygtis.

Nesunku parodyti, kad bet kurios kitos problemos sprendimas priklauso nuo vienos ar kelių pagrindinių problemų sprendimo. Apsvarstykite toliau pateiktas dvi problemas kaip pavyzdį.

1. Parašykite parabolės y = 2x 2 – 5x – 2 liestinių lygtis, jei liestinės susikerta stačiu kampu ir viena iš jų liečia parabolę taške su abscise 3 (5 pav.).

Sprendimas. Kadangi duota liestinės taško abscisė, pirmoji sprendimo dalis redukuojama į 1 pagrindinę problemą.

1. a = 3 – vienos iš stačiojo kampo kraštinių lietimo taško abscisė.
2. f(3) = 1.
3. f "(x) = 4x – 5, f "(3) = 7.
4. y = 1 + 7(x – 3), y = 7x – 20 – pirmosios liestinės lygtis.

Tegul a – pirmosios liestinės pasvirimo kampas. Kadangi liestinės yra statmenos, tai yra antrosios liestinės pasvirimo kampas. Iš lygties y = 7x – 20 pirmosios liestinės gauname tg a = 7. Raskime

Tai reiškia, kad antrosios liestinės nuolydis yra lygus .

Tolesnis sprendimas yra 3 pagrindinė užduotis.

Tada tegul B(c; f(c)) yra antrosios eilutės liesties taškas

1. – antrojo liesties taško abscisė.
2.
3.
4.
– antrosios liestinės lygtis.

Pastaba. Liestinės kampinį koeficientą lengviau rasti, jei mokiniai žino statmenų tiesių koeficientų santykį k 1 k 2 = – 1.

2. Užrašykite visų bendrųjų liestinių lygtis į funkcijų grafikus

Sprendimas. Užduotis yra surasti bendrųjų liestinių taškų abscises, tai yra išspręsti 1 pagrindinę problemą bendra forma, sudaryti lygčių sistemą ir tada ją išspręsti (6 pav.).

1. Funkcijos y = x 2 + x + 1 grafike esančio liestinės taško abscisė tebūna a.
2. f(a) = a 2 + a + 1.
3. f "(a) = 2a + 1.
4. y = a 2 + a + 1 + (2a + 1) (x – a) = (2a + 1)x + 1 – a 2 .

1. Funkcijos grafike esančio liestinės taško abscisė tegul c
2.
3. f "(c) = c.
4.

Kadangi liestinės yra bendrosios, tada

Taigi y = x + 1 ir y = – 3x – 3 yra bendrosios liestinės.

Pagrindinis nagrinėjamų užduočių tikslas – parengti studentus savarankiškai atpažinti esminės problemos tipą sprendžiant sudėtingesnes problemas, reikalaujančias tam tikrų tyrimo įgūdžių (gebėjimo analizuoti, lyginti, apibendrinti, kelti hipotezę ir kt.). Tokios užduotys apima bet kokią užduotį, kurios sudedamoji dalis yra pagrindinė užduotis. Panagrinėkime kaip pavyzdį funkciją (atvirkščiai 1 uždaviniui) rasti funkciją iš jos liestinių šeimos.

3. Kam b ir c yra funkcijos y = x 2 + bx + c grafiko liestinės y = x ir y = – 2x?

Sprendimas.

Tegul t yra tiesės y = x, kurios parabolė y = x 2 + bx + c, liesties taško abscisė; p yra tiesės y = – 2x, kai parabolė y = x 2 + bx + c, liesties taško abscisė. Tada liestinės lygtis y = x įgaus formą y = (2t + b)x + c – t 2 , o liestinės lygtis y = – 2x – y = (2p + b)x + c – p 2 .

Sudarykime ir išspręskime lygčių sistemą

Atsakymas:

Problemos, kurias reikia spręsti savarankiškai

1. Parašykite funkcijos y = 2x 2 – 4x + 3 grafiko liestinių lygtis grafiko susikirtimo su tiese y = x + 3 taškuose.

Atsakymas: y = – 4x + 3, y = 6x – 9,5.

2. Kokioms a reikšmėms funkcijos y = x 2 – ax grafiko liestinė grafiko taške, kurio abscisė x 0 = 1, eina per tašką M(2; 3)?

Atsakymas: a = 0,5.

3. Kokioms p reikšmėms tiesė y = px – 5 paliečia kreivę y = 3x 2 – 4x – 2?

Atsakymas: p 1 = – 10, p 2 = 2.

4. Raskite visus bendruosius funkcijos y = 3x – x 3 grafiko taškus ir šio grafiko liestinę, nubrėžtą per tašką P(0; 16).

Atsakymas: A(2; – 2), B(– 4; 52).

5. Raskite trumpiausią atstumą tarp parabolės y = x 2 + 6x + 10 ir tiesės

Atsakymas:

6. Kreivėje y = x 2 – x + 1 raskite tašką, kuriame grafiko liestinė yra lygiagreti tiesei y – 3x + 1 = 0.

Atsakymas: M(2; 3).

7. Užrašykite funkcijos y = x 2 + 2x – grafiko liestinės lygtį | 4x |, kuris paliečia jį dviejuose taškuose. Padarykite piešinį.

Atsakymas: y = 2x – 4.

8. Įrodykite, kad tiesė y = 2x – 1 nekerta kreivės y = x 4 + 3x 2 + 2x. Raskite atstumą tarp jų artimiausių taškų.

Atsakymas:

9. Parabolėje y = x 2 paimami du taškai, kurių abscisės x 1 = 1, x 2 = 3. Per šiuos taškus brėžiamas sekantas. Kuriame parabolės taške jos liestinė bus lygiagreti sekantui? Parašykite sekantines ir tangentines lygtis.

Atsakymas: y = 4x – 3 – sekantinė lygtis; y = 4x – 4 – liestinės lygtis.

10. Raskite kampą q tarp funkcijos y = x 3 – 4x 2 + 3x + 1 grafiko liestinių, nubrėžtų taškuose, kurių abscisės yra 0 ir 1.

Atsakymas: q = 45°.

11. Kuriuose taškuose funkcijos grafiko liestinė sudaro 135° kampą su Ox ašimi?

Atsakymas: A(0; – 1), B(4; 3).

12. Taške A(1; 8) į kreivę nubrėžiama liestinė. Raskite liestinės atkarpos tarp koordinačių ašių ilgį.

Atsakymas:

13. Užrašykite visų bendrųjų liestinių lygtį į funkcijų y = x 2 – x + 1 ir y = 2x 2 – x + 0,5 grafikus.

Atsakymas: y = – 3x ir y = x.

14. Raskite atstumą tarp funkcijos grafiko liestinių lygiagrečiai x ašiai.

Atsakymas:

15. Nustatykite, kokiais kampais parabolė y = x 2 + 2x – 8 kerta x ašį.

Atsakymas: q 1 = arctan 6, q 2 = arctan (– 6).

16. Funkcijų grafikas rasti visus taškus, kurių kiekvieno liestinė į šį grafiką kerta teigiamas koordinačių pusašis, nukirsdama nuo jų lygias atkarpas.

Atsakymas: A(– 3; 11).

17. Tiesė y = 2x + 7 ir parabolė y = x 2 – 1 susikerta taškuose M ir N. Raskite tiesių, liečiančių parabolę taškuose M ir N, susikirtimo tašką K.

Atsakymas: K(1; – 9).

18. Kokioms b reikšmėms tiesė y = 9x + b yra funkcijos y = x 3 – 3x + 15 grafiko liestinė?

Atsakymas: – 1; 31.

19. Kokioms k reikšmėms tiesė y = kx – 10 turi tik vieną bendras taškas su funkcijos y = 2x 2 + 3x – 2 grafiku? Rastoms k reikšmėms nustatykite taško koordinates.

Atsakymas: k 1 = – 5, A(– 2; 0); k 2 = 11, B(2; 12).

20. Kokioms b reikšmėms funkcijos y = bx 3 – 2x 2 – 4 grafiko liestinė taške, kurio abscisė x 0 = 2, eina per tašką M(1; 8)?

Atsakymas: b = – 3.

21. Parabolė, kurios viršūnė yra Ox ašyje, taške B liečia tiesę, einanti per taškus A(1; 2) ir B(2; 4). Raskite parabolės lygtį.

Atsakymas:

22. Kokia koeficiento k reikšme parabolė y = x 2 + kx + 1 liečia Ox ašį?

Atsakymas: k = d 2.

23. Raskite kampus tarp tiesės y = x + 2 ir kreivės y = 2x 2 + 4x – 3.

29. Raskite atstumą tarp funkcijos grafiko liestinių ir generatorių su teigiama Ox ašies kryptimi 45° kampu.

Atsakymas:

30. Raskite visų y = x 2 + ax + b formos parabolių, liestinių tiesės y = 4x – 1, viršūnių lokusą.

Atsakymas: tiesė y = 4x + 3.

Literatūra

1. Zvavich L.I., Shlyapochnik L.Ya., Chinkina M.V. Algebra ir analizės pradžia: 3600 uždavinių moksleiviams ir stojantiems į universitetus. – M., Bustardas, 1999 m.
2. Mordkovich A. Seminaras ketvertas jauniems mokytojams. Tema: Išvestinės programos. – M., „Matematika“, Nr.21/94.
3. Žinių ir įgūdžių formavimas remiantis psichikos veiksmų laipsniško įsisavinimo teorija. / Red. P.Ya. Galperina, N.F. Talyzina. – M., Maskvos valstybinis universitetas, 1968 m.

Šiame straipsnyje mes analizuosime visų tipų problemas, kurias reikia rasti

Prisiminkime geometrinė vedinio reikšmė: jei funkcijos grafike taške nubrėžta liestinė, tai liestinės nuolydžio koeficientas (lygus kampo tarp liestinės ir teigiamos ašies krypties liestims) yra lygus funkcijos išvestinei taške.

Paimkime savavališką liestinės tašką su koordinatėmis:

Ir apsvarstykite statųjį trikampį:

Šiame trikampyje

Iš čia

Tai yra taške nubrėžtos funkcijos grafiko liestinės lygtis.

Norėdami parašyti liestinės lygtį, turime žinoti tik funkcijos lygtį ir tašką, kuriame brėžiama liestinė. Tada galime rasti ir .

Yra trys pagrindiniai liestinių lygčių problemų tipai.

1. Suteiktas kontaktinis taškas

2. Pateikiamas liestinės nuolydžio koeficientas, tai yra funkcijos išvestinės taške reikšmė.

3. Duotos taško, per kurį nubrėžta liestinė, bet kuris nėra liesties taškas, koordinatės.

Pažvelkime į kiekvieno tipo užduotis.

1 . Parašykite funkcijos grafiko liestinės lygtį taške .

.

b) Raskite išvestinės reikšmę taške . Pirmiausia suraskime funkcijos išvestinę

Rastas reikšmes pakeiskime liestinės lygtimi:

Atidarykime skliaustus dešinėje lygties pusėje. Mes gauname:

Atsakymas: .

2. Raskite taškų, kuriuose funkcijos yra grafiko liestinės, abscises lygiagrečiai x ašiai.

Jei liestinė lygiagreti x ašiai, tai kampas tarp liestinės ir teigiamos ašies krypties lygus nuliui, taigi liestinės kampo liestinė lygi nuliui. Tai reiškia, kad funkcijos išvestinės reikšmė sąlyčio taškuose yra nulis.

a) Raskite funkcijos išvestinę .

b) Prilyginkime išvestinę nuliui ir raskime reikšmes, kuriose liestinė lygiagreti ašiai:

Prilyginus kiekvieną veiksnį nuliui, gauname:

Atsakymas: 0;3;5

3. Parašykite funkcijos grafiko liestinių lygtis , lygiagrečiai tiesiai .

Liestinė lygiagreti tiesei. Šios linijos nuolydis -1. Kadangi liestinė yra lygiagreti šiai linijai, liestinės nuolydis taip pat yra -1. Tai yra žinome liestinės nuolydį, taigi, išvestinė vertė liesties taške.

Tai yra antrojo tipo uždaviniai, norint rasti liestinės lygtį.

Taigi, mums duota funkcija ir išvestinės reikšmė liesties taške.

a) Raskite taškus, kuriuose funkcijos išvestinė lygi -1.

Pirmiausia suraskime išvestinę lygtį.

Išvestinę prilyginkime skaičiui -1.

Raskime funkcijos reikšmę taške.

(pagal sąlygą)

.

b) Raskite funkcijos grafiko liestinės taške lygtį.

Raskime funkcijos reikšmę taške.

(pagal sąlygą).

Pakeiskime šias reikšmes į liestinės lygtį:

.

Atsakymas:

4 . Parašykite kreivės liestinės lygtį , einantis per tašką

Pirmiausia patikrinkime, ar taškas yra liestinės taškas. Jei taškas yra liestinės taškas, tai jis priklauso funkcijos grafikui, o jo koordinatės turi tenkinti funkcijos lygtį. Pakeiskime taško koordinates į funkcijos lygtį.

Title="1sqrt(8-3^2)">. Мы получили под корнем !} neigiamas skaičius, lygybė nėra teisinga, o taškas nepriklauso funkcijos ir grafikui nėra sąlyčio taškas.

Tai paskutinis uždavinys, skirtas liestine lygčiai rasti. Pirmas dalykas turime rasti liestinės taško abscisę.

Raskime vertę.

Leiskite būti sąlyčio tašku. Taškas priklauso funkcijos grafiko liestinei. Jei šio taško koordinates pakeisime į liestinės lygtį, gausime teisingą lygybę:

.

Funkcijos reikšmė taške yra .

Raskime funkcijos išvestinės reikšmę taške.

Pirmiausia suraskime funkcijos išvestinę. Šis .

Išvestinė taške yra lygi .

Pakeiskime ir į liestinės lygtį. Gauname lygtį:

Išspręskime šią lygtį.

Sumažinkite trupmenos skaitiklį ir vardiklį 2:

Duokim dešinioji pusė lygtys su Bendras vardiklis. Mes gauname:

Supaprastinkime trupmenos skaitiklį ir padauginkime abi puses iš – ši išraiška yra griežtai didesnė už nulį.

Gauname lygtį

Išspręskime. Norėdami tai padaryti, išlyginkite abi dalis kvadratu ir pereikime prie sistemos.

Title="delim(lbrace)(matrica(2)(1)((64-48(x_0)+9(x_0)^2=8-(x_0)^2) (8-3x_0>=0 ) )) ( )">!}

Išspręskime pirmąją lygtį.

Nuspręskime kvadratinė lygtis, mes gauname

Antroji šaknis neatitinka sąlygos title="8-3x_0>=0">, следовательно, у нас только одна точка касания и её абсцисса равна .!}

Parašykime taško kreivės liestinės lygtį. Norėdami tai padaryti, pakeiskite reikšmę į lygtį – Jau įrašėme.

Atsakymas:
.

Liestinė yra tiesi linija , kuris paliečia funkcijos grafiką viename taške ir kurio visi taškai yra trumpiausiu atstumu nuo funkcijos grafiko. Todėl liestinė eina funkcijos grafiko liestine tam tikru kampu, o kelios liestinės skirtingais kampais negali praeiti per liesties tašką. Funkcijos grafiko liestinės ir normaliosios lygtys sudaromos naudojant išvestinę.

Tangentinė lygtis gaunama iš tiesės lygties .

Išveskime funkcijos grafiko liestinės lygtį, o tada normaliosios lygtį.

y = kx + b .

Jame k- kampo koeficientas.

Iš čia gauname tokį įrašą:

y - y 0 = k(x - x 0 ) .

Išvestinė vertė f "(x 0 ) funkcijas y = f(x) taške x0 lygus nuolydžiui k= tg φ per tašką nubrėžtos funkcijos grafiko liestinė M0 (x 0 , y 0 ) , Kur y0 = f(x 0 ) . Tai yra geometrinė vedinio reikšmė .

Taigi galime pakeisti kįjungta f "(x 0 ) ir gaukite šiuos dalykus funkcijos grafiko liestinės lygtis :

y - y 0 = f "(x 0 )(x - x 0 ) .

Esant uždaviniams, susijusiems su funkcijos grafiko liestinės lygties sudarymu (ir netrukus prie jų pereisime), reikia iš aukščiau pateiktos formulės gautą lygtį sumažinti iki bendrosios formos tiesės lygtis. Norėdami tai padaryti, turite perkelti visas raides ir skaičius į kairė pusė lygtį, o dešinėje pusėje palikite nulį.

Dabar apie normalią lygtį. Normalus - tai tiesi linija, einanti per funkcijos, statmenos liestinei, grafiko liesties tašką. Normali lygtis :

(x - x 0 ) + f "(x 0 )(y - y 0 ) = 0

Norėdami sušilti, jūsų prašoma pačiam išspręsti pirmąjį pavyzdį, o tada pažvelgti į sprendimą. Yra pagrindo tikėtis, kad ši užduotis mūsų skaitytojams nebus „šaltas dušas“.

0 pavyzdys. Sukurkite funkcijos taške grafikui liestinės lygtį ir normaliąją lygtį M (1, 1) .

1 pavyzdys. Parašykite funkcijos grafiko liestinės lygtį ir normaliąją lygtį , jei abscisė liestinė .

Raskime funkcijos išvestinę:

Dabar turime viską, ką reikia pakeisti į teorinės pagalbos įrašą, kad gautume liestinės lygtį. Mes gauname

Šiame pavyzdyje mums pasisekė: nuolydis buvo lygus nuliui, todėl lygtį atskirai sumažiname iki bendra išvaizda nebuvo reikalingas. Dabar galime sukurti normalią lygtį:

Žemiau esančiame paveikslėlyje: funkcijos grafikas bordo spalvos, liestinė Žalia spalva, oranžinė normali.

Kitas pavyzdys taip pat nesudėtingas: funkcija, kaip ir ankstesniame, taip pat yra daugianario, tačiau nuolydis nebus lygus nuliui, todėl bus pridėtas dar vienas žingsnis - lygties išvedimas į bendrą formą.

2 pavyzdys.

Sprendimas. Raskime liestinės taško ordinatę:

Raskime funkcijos išvestinę:

.

Raskime išvestinės reikšmę liestinės taške, tai yra liestinės nuolydį:

Visus gautus duomenis pakeičiame į „tuščią formulę“ ir gauname liestinės lygtį:

Pateikiame lygtį į bendrą formą (kairėje pusėje renkame visas raides ir skaičius, išskyrus nulį, o dešinėje paliekame nulį):

Sudarome normalią lygtį:

3 pavyzdys. Užrašykite funkcijos grafiko liestinės ir normaliosios lygtį, jei abscisė yra liesties taškas.

Sprendimas. Raskime liestinės taško ordinatę:

Raskime funkcijos išvestinę:

.

Raskime išvestinės reikšmę liestinės taške, tai yra liestinės nuolydį:

.

Randame liestinės lygtį:

Prieš pateikdami lygtį į bendrą formą, turite ją šiek tiek „šukuoti“: terminą iš termino padauginkite iš 4. Mes tai darome ir pateikiame lygtį į bendrą formą:

Sudarome normalią lygtį:

4 pavyzdys. Užrašykite funkcijos grafiko liestinės ir normaliosios lygtį, jei abscisė yra liesties taškas.

Sprendimas. Raskime liestinės taško ordinatę:

.

Raskime funkcijos išvestinę:

Raskime išvestinės reikšmę liestinės taške, tai yra liestinės nuolydį:

.

Gauname liestinės lygtį:

Pateikiame lygtį į bendrą formą:

Sudarome normalią lygtį:

Dažna klaida rašant tangentines ir normaliąsias lygtis yra nepastebėti, kad pavyzdyje pateikta funkcija yra sudėtinga, ir apskaičiuoti jos išvestinę kaip paprastos funkcijos išvestinę. Šie pavyzdžiai jau yra iš sudėtingos funkcijos(atitinkama pamoka atsidarys naujame lange).

5 pavyzdys. Užrašykite funkcijos grafiko liestinės ir normaliosios lygtį, jei abscisė yra liesties taškas.

Sprendimas. Raskime liestinės taško ordinatę:

Dėmesio! Ši funkcija- sudėtingas, nes liestinės argumentas (2 x) pati yra funkcija. Todėl funkcijos išvestinę randame kaip kompleksinės funkcijos išvestinę.