Katerikoli dve stranici paralelograma sta vzporedni. Paralelogram

Paralelogram je štirikotnik, katerega nasprotni strani sta v parih vzporedni (slika 233).

Za poljuben paralelogram veljajo naslednje lastnosti:

1. Nasprotni stranici paralelograma sta enaki.

Dokaz. V paralelogramu ABCD narišemo diagonalo AC. Trikotnika ACD in AC B sta enaka, saj imata skupno stranico AC in dva para enakih kotov ob njej:

(kot navzkrižni koti z vzporednima premicama AD in BC). To pomeni in tako kot stranice enakih trikotnikov ležijo nasproti enakih kotov, kar je bilo treba dokazati.

2. Nasprotna kota paralelograma sta enaka:

3. Sosednji koti paralelograma, tj. koti, ki mejijo na eno stran, seštejejo itd.

Dokaz lastnosti 2 in 3 dobimo takoj iz lastnosti kotov za vzporedne premice.

4. Diagonali paralelograma se razpolavljata v presečišču. Z drugimi besedami,

Dokaz. Trikotnika AOD in BOC sta skladna, saj sta njuni stranici AD in BC enaki (lastnost 1) in jima priležni koti (kot navzkrižni koti pri vzporednicah). Od tod sledi, da sta pripadajoči stranici teh trikotnikov enaki: AO, kar je bilo treba dokazati.

Vsaka od teh štirih lastnosti označuje paralelogram ali, kot pravijo, je njegova značilna lastnost, tj. vsak štirikotnik, ki ima vsaj eno od teh lastnosti, je paralelogram (in torej vse ostale tri lastnosti).

Dokaz opravimo za vsako nepremičnino posebej.

1". Če sta nasprotni strani štirikotnika v parih enaki, je štirikotnik paralelogram.

Dokaz. Naj ima štirikotnik ABCD stranice AD ​​in BC, AB in CD enake (slika 233). Narišimo diagonalo AC. Trikotnika ABC in CDA bosta enaka, kot da imata tri pare enake stranice.

Toda potem sta kota BAC in DCA enaka in . Vzporednost stranic BC in AD izhaja iz enakosti kotov CAD in ACB.

2. Če ima štirikotnik dva para nasprotnih kotov enaka, potem je to paralelogram.

Dokaz. Pustiti . Od takrat sta obe strani AD in BC vzporedni (glede na vzporednost premic).

3. Formulacijo in dokaz prepuščamo bralcu.

4. Če se diagonali štirikotnika v presečišču razpolovita, je štirikotnik paralelogram.

Dokaz. Če je AO = OS, BO = OD (slika 233), sta trikotnika AOD in BOC enaka, kot da imata enaki koti(navpično!) v oglišču O, zaprtem med pari enakih stranic AO in CO, BO in DO. Iz enakosti trikotnikov sklepamo, da sta stranici AD in BC enaki. Stranici AB in CD sta prav tako enaki in štirikotnik se glede na značilno lastnost G izkaže za paralelogram.

Torej, da bi dokazali, da je dani štirikotnik paralelogram, je dovolj, da preverimo veljavnost katere koli od štirih lastnosti. Bralec je povabljen, da samostojno dokaže še eno značilno lastnost paralelograma.

5. Če ima štirikotnik par enakih, vzporednih stranic, potem je to paralelogram.

Včasih katerikoli par vzporednih stranic paralelograma imenujemo njegove osnove, drugi dve pa stranski stranici. Odsek ravne črte, ki je pravokoten na dve stranici paralelograma in je zaprt med njima, se imenuje višina paralelograma. Paralelogram na sl. 234 ima višino h, narisano na straneh AD in BC, drugo višino predstavlja segment .

Koncept paralelograma

Definicija 1

Paralelogram je štirikotnik, v katerem sta nasprotni stranici vzporedni med seboj (slika 1).

Slika 1.

Paralelogram ima dve glavni lastnosti. Upoštevajmo jih brez dokazov.

Lastnost 1: Nasprotni strani in koti paralelograma so enaki.

Lastnost 2: V paralelogramu narisane diagonale se razpolovijo s presečiščem.

Znaki paralelograma

Razmislimo o treh značilnostih paralelograma in jih predstavimo v obliki izrekov.

1. izrek

Če sta dve stranici štirikotnika med seboj enaki in hkrati vzporedni, bo ta štirikotnik paralelogram.

Dokaz.

Naj nam bo dan štirikotnik $ABCD$. V katerem $AB||CD$ in $AB=CD$ Vanj narišimo diagonalo $AC$ (slika 2).

Slika 2.

Razmislite o vzporednih premicah $AB$ in $CD$ ter njuni sekanti $AC$. Potem

\[\kot CAB=\kot DCA\]

kot prekrižani vogali.

Po $I$ kriteriju enakosti trikotnikov je

ker je $AC$ njuna skupna stranica, $AB=CD$ pa po pogoju. Pomeni

\[\kot DAC=\kot ACB\]

Oglejmo si premici $AD$ in $CB$ ter njun sekant $AC$; z zadnjo enakostjo med ležečima kotoma dobimo, da je $AD||CB$.) Posledično je po definiciji $1$ ta štirikotnik paralelogram.

Izrek je dokazan.

2. izrek

Če sta nasprotni stranici štirikotnika enaki, je štirikotnik paralelogram.

Dokaz.

Naj nam bo dan štirikotnik $ABCD$. Pri čemer je $AD=BC$ in $AB=CD$. Vanj narišimo diagonalo $AC$ (slika 3).

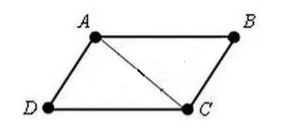
Slika 3.

Ker je $AD=BC$, $AB=CD$ in $AC$ skupna stranica, potem po kriteriju $III$ za enakost trikotnikov velja

\[\trikotnik DAC=\trikotnik ACB\]

\[\kot DAC=\kot ACB\]

Oglejmo si premici $AD$ in $CB$ ter njuno sekanto $AC$; z zadnjo enakostjo med ležečima kotoma dobimo $AD||CB$. Zato je po definiciji $1$ ta štirikotnik paralelogram.

\[\kot DCA=\kot CAB\]

Oglejmo si premici $AB$ in $CD$ ter njuno sekanto $AC$; z zadnjo enakostjo med ležečima kotoma dobimo $AB||CD$. Zato je po definiciji 1 ta štirikotnik paralelogram.

Izrek je dokazan.

Izrek 3

Če so štirikotniku narisane diagonale s presečiščem razdeljene na dva enaka dela, je ta štirikotnik paralelogram.

Dokaz.

Naj nam bo dan štirikotnik $ABCD$. Vanj narišimo diagonali $AC$ in $BD$. Naj se sekata v točki $O$ (slika 4).

Slika 4.

Ker je po pogoju $BO=OD,\ AO=OC$ in so koti $\angle COB=\angle DOA$ navpični, potem je po $I$ kriteriju za enakost trikotnikov

\[\trikotnik BOC=\trikotnik AOD\]

\[\kot DBC=\kot BDA\]

Oglejmo si premici $BC$ in $AD$ ter njuno sekanto $BD$; z zadnjo enakostjo med ležečima kotoma dobimo $BC||AD$. Tudi $BC=AD$. Zato je po izreku $1$ ta štirikotnik paralelogram.

Tako kot sta v evklidski geometriji točka in premica glavna elementa teorije ravnin, je paralelogram ena ključnih figur konveksnih štirikotnikov. Iz njega, kot niti iz krogle, tečejo koncepti "pravokotnik", "kvadrat", "romb" in druge geometrijske količine.

V stiku z

Definicija paralelograma

konveksni štirikotnik, sestavljen iz segmentov, od katerih je vsak par vzporeden, je v geometriji znan kot paralelogram.

Kako izgleda klasični paralelogram, prikazuje štirikotnik ABCD. Stranice imenujemo osnovke (AB, BC, CD in AD), navpičnico, ki poteka iz poljubnega oglišča na stranico, ki je nasproti tega oglišča, imenujemo višina (BE in BF), premici AC in BD imenujemo diagonali.

Pozor! Kvadrat, romb in pravokotnik so posebni primeri paralelograma.

Strani in koti: značilnosti razmerja

Ključne lastnosti na splošno vnaprej določeno s samo oznako, jih dokazuje izrek. Te značilnosti so naslednje:

1. Stranici, ki sta si nasproti, sta v parih enaki.
2. Nasprotni koti so v parih enaki.

Dokaz: Vzemimo ∆ABC in ∆ADC, ki ju dobimo, če štirikotnik ABCD razdelimo s premico AC. ∠BCA=∠CAD in ∠BAC=∠ACD, saj jima je AC skupen (navpična kota za BC||AD oziroma AB||CD). Iz tega sledi: ∆ABC = ∆ADC (drugi znak enakosti trikotnikov).

Dolžici AB in BC v ∆ABC v paru ustrezata daljici CD in AD v ∆ADC, kar pomeni, da sta enaki: AB = CD, BC = AD. Tako ∠B ustreza ∠D in sta enaka. Ker je ∠A=∠BAC+∠CAD, ∠C=∠BCA+∠ACD, ki sta prav tako po paru enaka, potem je ∠A = ∠C. Lastnost je dokazana.

Značilnosti diagonal figure

Glavna značilnost teh premic paralelograma: presečišče jih deli na pol.

Dokaz: Naj bo i.e. presečišče diagonal AC in BD lika ABCD. Tvorita dva sorazmerna trikotnika - ∆ABE in ∆CDE.

AB=CD, ker sta nasprotni. Glede na premico in sekanto je ∠ABE = ∠CDE in ∠BAE = ∠DCE.

Po drugem kriteriju enakosti je ∆ABE = ∆CDE. To pomeni, da sta elementa ∆ABE in ∆CDE: AE = CE, BE = DE in sta hkrati sorazmerna dela AC in BD. Lastnost je dokazana.

Značilnosti sosednjih vogalov

Sosednji stranici imata vsoto kotov 180°, saj ležita na isti strani vzporednic in prečnice. Za štirikotnik ABCD:

∠A+∠B=∠C+∠D=∠A+∠D=∠B+∠C=180º

Lastnosti simetrale:

1. , spuščeni na eno stran, so pravokotni;
2. nasprotni oglišči imata vzporedne simetrale;
3. trikotnik, ki ga dobimo, če narišemo simetralo, bo enakokrak.

Določanje značilnih lastnosti paralelograma s pomočjo izreka

Značilnosti te figure izhajajo iz glavnega izreka, ki pravi naslednje: štirikotnik velja za paralelogram v primeru, da se njegove diagonale sekajo in jih ta točka razdeli na enake segmente.

Dokaz: naj se premici AC in BD štirikotnika ABCD sekata v t.j. Ker je ∠AED = ∠BEC in je AE+CE=AC BE+DE=BD, potem je ∆AED = ∆BEC (po prvem kriteriju enakosti trikotnikov). To je ∠EAD = ∠ECB. So tudi notranji prečni koti sekante AC za premici AD in BC. Tako po definiciji paralelizma - AD || B.C. Izvedena je tudi podobna lastnost premic BC in CD. Izrek je dokazan.

Izračun površine figure

Območje te figure najdemo z več metodami eden najpreprostejših: množenje višine in osnove, na katero je narisana.

Dokaz: iz oglišč B in C nariši navpičnici BE in CF. ∆ABE in ∆DCF sta enaka, saj je AB = CD in BE = CF. ABCD je po velikosti enak pravokotniku EBCF, saj sta sestavljena iz sorazmernih likov: S ABE in S EBCD ter S DCF in S EBCD. Iz tega izhaja, da je območje tega geometrijski lik se nahaja na enak način kot pravokotnik:

S ABCD = S EBCF = BE×BC=BE×AD.

Za določitev splošne formule za površino paralelograma označimo višino kot hb, in stran - b. Oziroma:

Drugi načini za iskanje območja

Izračuni površin skozi stranice paralelograma in kot, ki ga tvorijo, je druga znana metoda.

,

Spr-ma - območje;

a in b sta njegovi stranici

α je kot med segmentoma a in b.

Ta metoda praktično temelji na prvi, vendar v primeru, da ni znana. vedno odreže pravokotni trikotnik, katerega parametri so najdeni trigonometrične identitete, to je . S preoblikovanjem relacije dobimo . V enačbi prve metode nadomestimo višino s tem produktom in dobimo dokaz o veljavnosti te formule.

Skozi diagonali paralelograma in kot, ki jih ustvarijo, ko se sekajo, lahko najdete tudi območje.

Dokaz: AC in BD se sekata in tvorita štiri trikotnike: ABE, BEC, CDE in AED. Njihova vsota je enaka površini tega štirikotnika.

Ploščino vsakega od teh ∆ je mogoče najti z izrazom , kjer je a=BE, b=AE, ∠γ =∠AEB. Ker je za izračune uporabljena ena sinusna vrednost. To je . Ker je AE+CE=AC= d 1 in BE+DE=BD= d 2, se formula ploščine zmanjša na:

.

Uporaba v vektorski algebri

Značilnosti sestavnih delov tega štirikotnika so našle uporabo v vektorski algebri, in sicer seštevanje dveh vektorjev. Pravilo paralelograma pravi, da če so podani vektorjiinnekolinearni, potem bo njihova vsota enaka diagonali te figure, katere osnove ustrezajo tem vektorjem.

Dokaz: iz poljubno izbranega začetka - t.j. - konstruirati vektorje in . Nato sestavimo paralelogram OASV, kjer sta odseka OA in OB stranice. Tako OS leži na vektorju ali vsoti.

Formule za izračun parametrov paralelograma

Identitete so podane pod naslednjimi pogoji:

1. a in b, α - stranice in kot med njimi;
2. d 1 in d 2, γ - diagonali in na mestu njihovega presečišča;
3. h a in h b - višine, spuščene na strani a in b;

Parameter	Formula
Iskanje strani
vzdolž diagonal in kosinus kota med njima
vzdolž diagonal in stranic
skozi višino in nasprotno oglišče
Iskanje dolžin diagonal
na straneh in velikost konice med njimi

Sign-ki pa-ral-le-lo-gram-ma

1. Definicija in osnovne lastnosti paralelograma

Začnimo s priklicem definicije para-ral-le-lo-grama.

Opredelitev. Paralelogram- what-you-rekh-gon-nick, ki ima vsaki dve pro-ti-false strani, ki sta vzporedni (glej sliko 1).

riž. 1. Pa-ral-le-lo-gram

Spomnimo se osnovne lastnosti pa-ral-le-lo-gram-ma:

Da bi lahko uporabili vse te lastnosti, morate biti prepričani, da fi-gu-ra, o nekom -Roy govorimo o, - pa-ral-le-lo-gram. Da bi to naredili, je treba poznati takšna dejstva, kot so znaki pa-ral-le-lo-gram-ma. Zdaj si ogledujemo prva dva.

2. Prvi znak paralelograma

Izrek. Prvi znak pa-ral-le-lo-gram-ma.Če sta v štirih premogih dve nasprotni strani enaki in vzporedni, potem je ta vzdevek štirih premogov - paralelogram. .

riž. 2. Prvi znak pa-ral-le-lo-gram-ma

Dokaz. Postavimo dia-go-nal v štiri-reh-coal-ni-ka (glej sliko 2), ona ga je razdelila na dve tri-coal-ni-ka. Zapišimo, kaj vemo o teh trikotnikih:

glede na prvi znak enakosti trikotnikov.

Iz enakosti navedenih trikotnikov sledi, da z znakom vzporednosti ravnih črt pri prečkanju ch-nii njihove s-ku-shchi. To imamo:

Do-ka-za-ampak.

3. Drugi znak paralelograma

Izrek. Drugi znak je pa-ral-le-lo-gram-ma.Če sta v štirikotniku vsaka dva pro-ti-lažna stranica enaka, potem je ta štirikotnik paralelogram. .

riž. 3. Drugi znak pa-ral-le-lo-gram-ma

Dokaz. Dia-go-nal postavimo v štirikotnik (glej sliko 3), ona ga razdeli na dva trikotnika. Zapišimo, kaj vemo o teh trikotnikih glede na obliko teorije:

po tretjem znaku enakosti trikotnikov.

Iz enakosti trikotnikov sledi, da z znakom vzporednih črt, ko jih sekajo s-ku-shchey. Jejmo:

par-ral-le-lo-gram po definiciji. Q.E.D.

Do-ka-za-ampak.

4. Primer uporabe prve lastnosti paralelograma

Oglejmo si primer uporabe znakov pa-ral-le-lo-gram.

Primer 1. V izboklini ni oglja Poiščite: a) vogale oglja; b) sto-ro-dobro.

rešitev. Ilustracija Fig. 4.

pa-ral-le-lo-gram glede na prvi znak pa-ral-le-lo-gram-ma.

A. z lastnostjo par-ral-le-lo-grama o pro-ti-lažnih kotih, z lastnostjo par-ral-le-lo-grama o vsoti kotov, ko leži na eni strani.

B. po naravi enakosti pro-lažnih strani.

re-tiy znak pa-ral-le-lo-gram-ma

5. Ponovi: Definicija in lastnosti paralelograma

Zapomnimo si to paralelogram- to je štirikotnik, ki ima nasprotne stranice v parih. To je, če - par-ral-le-lo-gram, potem (glej sliko 1).

Parallel-le-lo-gram ima številne lastnosti: nasprotna kota sta enaka (), nasprotna kota -smo enaki ( ). Poleg tega je dia-go-na-li pa-ral-le-lo-gram-ma na točki re-se-che-niya razdeljen glede na vsoto kotov, pri-le-pressing na kateri koli stranska pa-ral-le-lo-gram-ma, enaka itd.

Toda, da bi izkoristili vse te lastnosti, je treba biti popolnoma prepričan, da je ri-va-e-my th-you-rekh-coal-nick - pa-ral-le-lo-gram. V ta namen obstajajo znaki par-ral-le-lo-grama: to so tista dejstva, iz katerih je mogoče potegniti enoznačen zaključek, da je tisto, kar-ti-rekh-coal-nick par-ral- le-lo-gram-mama. V prejšnji lekciji smo si že ogledali dva znaka. Zdaj gledamo tretji čas.

6. Tretje znamenje paralelograma in njegov dokaz

Če je v štirih premogih dia-go-on na točki re-se-che-niya do-by-lams, potem je dani štiri-vas Roh-coal-nick pa-ral-le -lo-gram-mama.

podano:

Kaj-si-premog-nick; ; .

Dokaži:

Paralelogram.

Dokaz:

Da bi dokazali to dejstvo, je treba pokazati vzporednost strank v par-le-lo-gramu. In vzporednost ravnih črt se najpogosteje doseže z enakostjo notranjih navzkrižnih kotov pri teh pravih kotih. Tako je tukaj naslednja metoda za pridobitev tretjega znaka par-ral -le-lo-gram-ma: z enakostjo trikotnikov .

Poglejmo, kako so ti trikotniki enaki. Dejansko iz pogoja sledi: . Poleg tega sta kota enaka, ker sta navpična. To je:

(prvi znak enakostitri-premog-ni-cov- vzdolž dveh stranic in vogala med njima).

Iz enakosti trikotnikov: (ker so notranji navzkrižni koti pri teh premicah in ločilih enaki). Poleg tega iz enakosti trikotnikov sledi, da . To pomeni, da razumemo, da je v štirih premogih dvesto enakih in vzporednih. Glede na prvi znak, pa-ral-le-lo-gram-ma: - pa-ral-le-lo-gram.

Do-ka-za-ampak.

7. Primer naloge o tretjem znaku paralelograma in posploševanje

Poglejmo primer uporabe tretjega znaka pa-ral-le-lo-grama.

Primer 1

podano:

- paralelogram; . - se-re-di-na, - se-re-di-na, - se-re-di-na, - se-re-di-na (glej sliko 2).

Dokaži:- pa-ral-le-lo-gram.

Dokaz:

To pomeni, da v štiri-premog-no-dia-go-on-ali na točki re-se-che-niya naredijo-by-lam. S tretjim znakom pa-ral-le-lo-grama iz tega sledi - pa-ral-le-lo-gram.

Do-ka-za-ampak.

Če analizirate tretji znak pa-ral-le-lo-grama, potem lahko opazite, da je ta znak s-vet- ima lastnost par-ral-le-lo-grama. To pomeni dejstvo, da dia-go-na-li de-la-xia ni le lastnost par-le-lo-grama in njegovega razlikovalnega, kha-rak-te-ri-sti-che- lastnost, po kateri se lahko loči od niza what-you-rekh-coal-ni-cov.

VIR

http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/priznaki-parallelogramma

http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/tretiy-priznak-parallelogramma

http://www.uchportfolio.ru/users_content/675f9820626f5bc0afb47b57890b466e/images/46TThxQ8j4Y.jpg

http://cs10002.vk.me/u31195134/116260458/x_56d40dd3.jpg

http://www.tepka.ru/geometriya/16.1.gif

Paralelogram je štirikotnik, katerega nasprotni strani sta v parih vzporedni. Naslednja slika prikazuje paralelogram ABCD. Ima stranico AB vzporedno s stranico CD in stranico BC vzporedno s stranico AD.

Kot ste morda uganili, je paralelogram konveksen štirikotnik. Razmislimo o osnovnih lastnostih paralelograma.

Lastnosti paralelograma

1. V paralelogramu so nasprotni koti in nasprotne stranice enaki. Dokažimo to lastnost – razmislimo o paralelogramu, predstavljenem na naslednji sliki.

Diagonala BD ga deli na dvoje enak trikotnik: ABD in CBD. Vzdolž stranice BD in obeh kotov, ki ležita na njej, sta enaka, saj sta kota, ki navzkrižno ležita na sekanti BD vzporednic BC in AD oziroma AB in CD. Zato je AB = CD in
pr. Kr. = AD. In iz enakosti kotov 1, 2, 3 in 4 sledi, da je kot A = kot 1 + kot 3 = kot 2 + kot 4 = kot C.

2. Diagonali paralelograma sta razdeljeni na pol s presečiščem. Naj bo točka O presečišče diagonal AC in BD paralelograma ABCD.

Potem sta si trikotnik AOB in trikotnik COD enaka, vzdolž stranice in dveh sosednjih kotov. (AB = CD, ker sta to nasprotni strani paralelograma. In kot 1 = kot 2 in kot 3 = kot 4 sta kot navzkrižna kota, ko premici AB in CD sekata sekanti AC oziroma BD.) Iz tega sledi, da je AO = OC in OB = OD, kar je bilo treba dokazati.

Vse glavne lastnosti so prikazane na naslednjih treh slikah.