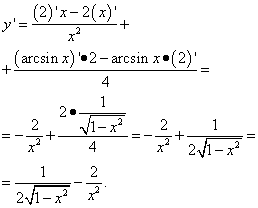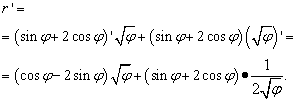Derivát kosínusu: (cos x)′. Derivácie goniometrických funkcií: tangens, sínus, kosínus a iné

Nájdite derivát.

Možnosť 1.

Možnosť 2.

pri = 2X + 5.

pri = 2X – 5.

pri= 4 cos X.

pri= 3 hriechy X.

pri= tg X+ctg X.

pri= tg X-ctg X.

pri= hriech 3 X.

pri= čo 4 X.

Možnosti odpovede.

– 4 hriechy X

– 3 cos X

1/cos 2 X+ 1/hriech 2 X

1/cos 2 X-1/hriech 2 X

1/hriech 2 X-1/cos 2 X

- 4 sin4 X

– 3cos3 X

f(X) = hriech X+ cos X

f(X) = hriech 2 X – X

f(X) = 2X+cos(4 X – )

možnosť 1

Možnosť 2

r = 2X 3

r = 3X 2

r = 1/4 X 4 + 2X 2 – 7

r = 1/2 X 4 + 4X + 5

r = X 3 + 4X 2 – 3X.
Vyriešte rovnicu r " = 0

r = 2X 3 – 9X 2 + 12X + 7.
Vyriešte rovnicu r " = 0.

r= hriech 2 X– pretože 3 X.

r= čo 2 X- hriech 3 X.

r= tg X–ctg( X + /4).

r=ctg X+ tg( X – /4).

r= hriech 2 X.

r= čo 2 X.

Možnosti odpovede.

Pri odvodení úplne prvého vzorca tabuľky budeme vychádzať z definície derivačnej funkcie v bode. Vezmime kam X- akýkoľvek Reálne číslo, teda X– ľubovoľné číslo z oblasti definície funkcie. Zapíšme si limit pomeru prírastku funkcie k prírastku argumentu na :

Treba poznamenať, že pod medzným znamienkom sa získa výraz, ktorým nie je neistota nuly delená nulou, keďže v čitateli nie je nekonečne malá hodnota, ale práve nula. Inými slovami, prírastok konštantnej funkcie je vždy nula.

teda derivácia konštantnej funkciesa rovná nule v celej oblasti definície.

Derivácia mocninovej funkcie.

Vzorec pre deriváciu mocninnej funkcie má tvar , kde exponent p– akékoľvek reálne číslo.

Dokážme najprv vzorec pre prirodzený exponent, teda pre p = 1, 2, 3, …

Použijeme definíciu derivátu. Zapíšme si limitu pomeru prírastku mocninnej funkcie k prírastku argumentu:

Na zjednodušenie výrazu v čitateli sa obraciame na Newtonov binomický vzorec:

teda

To dokazuje vzorec pre deriváciu mocninnej funkcie pre prirodzený exponent.

Derivácia exponenciálnej funkcie.

Uvádzame odvodenie derivačného vzorca na základe definície:

Dostali sme sa do neistoty. Na jej rozšírenie uvádzame novú premennú a na adrese . Potom . Pri poslednom prechode sme použili vzorec na prechod na nový logaritmický základ.

Dosadíme do pôvodného limitu:

Ak si spomenieme na druhú pozoruhodnú limitu, dostaneme sa k vzorcu pre deriváciu exponenciálnej funkcie:

Derivácia logaritmickej funkcie.

Dokážme vzorec pre deriváciu logaritmickej funkcie pre všetkých X z domény definície a všetkých platných hodnôt bázy a logaritmus Podľa definície derivátu máme:

Ako ste si všimli, počas dôkazu sa transformácie vykonávali pomocou vlastností logaritmu. Rovnosť je pravda vďaka druhej pozoruhodnej hranici.

Derivácie goniometrických funkcií.

Aby sme odvodili vzorce pre derivácie goniometrických funkcií, budeme si musieť pripomenúť niektoré trigonometrické vzorce, ako aj prvú pozoruhodnú limitu.

Podľa definície derivácie pre funkciu sínus máme .

Použime vzorec rozdielu sínusov:

Zostáva sa obrátiť na prvý pozoruhodný limit:

Teda derivácia funkcie hriech x Existuje cos x.

Vzorec pre deriváciu kosínusu je dokázaný presne rovnakým spôsobom.

Preto derivácia funkcie cos x Existuje - hriech x.

Vzorce pre tabuľku derivácií pre tangens a kotangens odvodíme pomocou osvedčených pravidiel diferenciácie (derivácia zlomku).

Deriváty hyperbolických funkcií.

Pravidlá diferenciácie a vzorec pre deriváciu exponenciálnej funkcie z tabuľky derivácií nám umožňujú odvodiť vzorce pre derivácie hyperbolického sínusu, kosínusu, tangensu a kotangensu.

Derivácia inverznej funkcie.

Aby sme predišli zmätku pri prezentácii, označme argument funkcie, pomocou ktorej sa vykonáva diferenciácia, dolným indexom, to znamená, že ide o deriváciu funkcie. f(x) Autor: X.

Teraz poďme formulovať pravidlo na nájdenie derivácie inverznej funkcie.

Nechajte funkcie y = f(x) A x = g(y) vzájomne inverzné, definované na intervaloch resp. Ak v určitom bode existuje konečná nenulová derivácia funkcie f(x), potom v bode existuje konečná derivácia inverznej funkcie g(y), a . V inom príspevku .

Toto pravidlo je možné preformulovať pre kohokoľvek X z intervalu , potom dostaneme .

Overme si platnosť týchto vzorcov.

Nájdite inverznú funkciu pre prirodzený logaritmus (Tu r je funkcia a X- argument). Po vyriešení tejto rovnice pre X, dostaneme (tu X je funkcia a r– jej argument). teda a vzájomne inverzné funkcie.

Z tabuľky derivátov to vidíme A .

Uistime sa, že vzorce na nájdenie derivátov inverznej funkcie nás vedú k rovnakým výsledkom:

Uvádza sa dôkaz a odvodenie vzorca pre deriváciu kosínusu - cos(x). Príklady výpočtu derivácií cos 2x, cos 3x, cos nx, cosínus na druhú, kubická a na mocninu n. Vzorec pre deriváciu kosínusu n-tého rádu.

Derivácia vzhľadom na premennú x od kosínusu x sa rovná mínus sínusu x:
(cos x)′ = - hriech x.

Dôkaz

Na odvodenie vzorca pre deriváciu kosínusu používame definíciu derivácie:
.

Transformujme tento výraz, aby sme ho zredukovali na známe matematické zákony a pravidlá. Na to potrebujeme poznať štyri vlastnosti.
1) Goniometrické vzorce. Budeme potrebovať nasledujúci vzorec:
(1) ;
2) Vlastnosť spojitosti funkcie sínus:
(2) ;
3) Význam prvého pozoruhodného limitu:
(3) ;
4) Vlastnosť limity súčinu dvoch funkcií:
Ak a potom
(4) .

Aplikujme tieto zákony na naše limity. Najprv transformujeme algebraický výraz
.
Na tento účel použijeme vzorec
(1) ;
V našom prípade
; . Potom
;
;
;
.

Urobme náhradu. V , . Používame vlastnosť spojitosti (2):
.

Urobme rovnakú substitúciu a použijeme prvý pozoruhodný limit (3):
.

Keďže existujú vyššie vypočítané limity, použijeme vlastnosť (4):

.

Takto sme získali vzorec pre deriváciu kosínusu.

Príklady

Uvažujme jednoduché príklady hľadanie derivátov funkcií obsahujúcich kosínus. Poďme nájsť deriváty nasledujúce funkcie:
y = cos 2x; y = cos 3x; y = cos nx; y = čo 2 x; y = čo 3 x a y = cos n x.

Príklad 1

Nájdite deriváty čo 2x, čo 3x A cosnx.

Riešenie

Pôvodné funkcie majú podobnú formu. Preto nájdeme deriváciu funkcie y = cosnx. Potom, ako derivát cosnx, dosaďte n = 2 an = 3 . A tak získame vzorce pre deriváty čo 2x A čo 3x .

Nájdeme teda deriváciu funkcie
y = cosnx .
Predstavme si túto funkciu premennej x ako komplexnú funkciu pozostávajúcu z dvoch funkcií:
1)
2)
Pôvodná funkcia je potom komplexná (zložená) funkcia zložená z funkcií a:
.

Nájdite deriváciu funkcie vzhľadom na premennú x:
.
Nájdite deriváciu funkcie vzhľadom na premennú:
.
Aplikujeme.
.
Nahradíme:
(P1) .

Teraz vo vzorci (A1) nahradíme a:
;
.

Odpoveď

;
;
.

Príklad 2

Nájdite deriváty kosínu na druhú, kosínu na druhú a kosínusu k mocnine n:
y = čo 2 x; y = čo 3 x; y = cos n x.

Riešenie

V tomto príklade majú funkcie tiež podobný vzhľad. Preto nájdeme derivát z najviac všeobecná funkcia- kosínus na mocninu n:
y = cos n x.
Potom dosadíme n = 2 a n = 3. A tak získame vzorce pre deriváty kosínu na druhú a kosínus na mocninu.

Musíme teda nájsť deriváciu funkcie
.
Prepíšme to do zrozumiteľnejšej podoby:
.
Predstavme si túto funkciu ako komplexnú funkciu pozostávajúcu z dvoch funkcií:
1) Funkcie závislé od premennej: ;
2) Funkcie závislé od premennej: .
Pôvodná funkcia je potom komplexná funkcia zložená z dvoch funkcií a :
.

Nájdite deriváciu funkcie vzhľadom na premennú x:
.
Nájdite deriváciu funkcie vzhľadom na premennú:
.
Uplatňujeme pravidlo diferenciácie komplexných funkcií.
.
Nahradíme:
(P2) .

Teraz nahraďme a:
;
.

Odpoveď

;
;
.

Deriváty vyššieho rádu

Všimnite si, že derivát cos x prvý rád možno vyjadriť pomocou kosínu takto:
.

Nájdite deriváciu druhého rádu pomocou vzorca pre deriváciu komplexnej funkcie:

.
Tu .

Všimnite si tú diferenciáciu cos x spôsobí zvýšenie jeho argumentu o . Potom derivácia n-tého rádu má tvar:
(5) .

Tento vzorec možno prísnejšie dokázať pomocou metódy matematickej indukcie. Dôkaz n-tej derivácie sínusu je uvedený na stránke „Derivácia sínusu“. Pre n-tú deriváciu kosínusu je dôkaz úplne rovnaký. Musíte len nahradiť hriech s cos vo všetkých vzorcoch.

Prezentované sú derivácie inverzných goniometrických funkcií a odvodenie ich vzorcov. Uvádzajú sa aj výrazy pre deriváty vyššieho rádu. Odkazy na stránky s podrobnejším popisom odvodzovania vzorcov.

Najprv odvodíme vzorec pre deriváciu arcsínusu. Nechaj
y = arcsin x.
Keďže arcsínus je inverzná funkcia sínusu
.
Tu je y funkciou x. Diferencujte vzhľadom na premennú x:
.
Aplikujeme:
.
Tak sme našli:
.

Pretože teda. Potom
.
A predchádzajúci vzorec má tvar:
. Odtiaľ
.

Presne týmto spôsobom môžete získať vzorec pre deriváciu arckosínusu. Jednoduchšie je však použiť vzorec týkajúci sa inverzných goniometrických funkcií:
.
Potom
.

Podrobnejší popis je uvedený na stránke „Odvodenie derivátov arczínu a arkozínu“. Tam je to dané odvodenie derivátov dvoma spôsobmi- diskutované vyššie a podľa vzorca pre deriváciu inverznej funkcie.

Odvodenie derivátov arkustangens a arkotangens

Rovnakým spôsobom nájdeme deriváty arkustangens a arkotangens.

Nechaj
y = arctan x.
Arktangens je inverzná funkcia tangensu:
.
Diferencujte vzhľadom na premennú x:
.
Použijeme vzorec pre deriváciu komplexnej funkcie:
.
Tak sme našli:
.

Derivát oblúkového kotangens:
.

Deriváty arkzínu

Nechaj
.
Už sme našli derivát prvého rádu arcsínusu:
.
Diferencovaním nájdeme derivát druhého rádu:
;
.
Môže byť napísaný aj v tejto forme:
.
Odtiaľ dostaneme diferenciálnu rovnicu, ktorá je splnená arcsínusovými deriváciami prvého a druhého rádu:
.

Diferencovaním tejto rovnice môžeme nájsť derivácie vyššieho rádu.

Derivácia arcsínusu n-tého rádu

Derivácia arcsínusu rádu n má ďalší pohľad:
,
kde je polynóm stupňa . Určuje sa podľa vzorcov:
;
.
Tu .

Polynóm vyhovuje diferenciálnej rovnici:
.

Derivát arkozínu n-tého rádu

Deriváty pre arccosínus sa získajú z derivátov pre arc sínus pomocou trigonometrického vzorca:
.
Preto sa deriváty týchto funkcií líšia iba znamienkom:
.

Deriváty arkustangens

Nechaj . Našli sme deriváciu oblúkového kotangensu prvého rádu:
.

Rozložme zlomok na najjednoduchšiu formu:

.
Tu je pomyselná jednotka, .

Raz diferencujeme a zlomok privedieme k spoločnému menovateľovi:

.

Nahradením dostaneme:
.

Derivácia arkustangens n-tého rádu

Deriváciu arkustangensu n-tého rádu možno teda reprezentovať niekoľkými spôsobmi:
;
.

Deriváty oblúkového kotangensu

Nech je to teraz. Použime vzorec spájajúci inverzné goniometrické funkcie:
.
Potom sa derivácia arkustangensu n-tého rádu líši od derivácie arkustangensu iba znamienkom:
.

Nahradením nájdeme:
.

Referencie:
N.M. Gunter, R.O. Kuzmin, Zbierka úloh z vyššej matematiky, „Lan“, 2003.

Nájsť derivácia goniometrickej funkcie treba použiť tabuľku derivátov, a to deriváty 6-13.

Keď nájdete derivácie jednoduchých goniometrických funkcií Aby ste sa vyhli bežným chybám, mali by ste venovať pozornosť nasledujúcim bodom:

• vo výraze funkcie je často jeden z výrazov sínus, kosínus alebo iná goniometrická funkcia nie z argumentu funkcie, ale z čísla (konštanty), preto sa derivácia tohto členu rovná nule;
• takmer vždy musíte zjednodušiť výraz získaný v dôsledku diferenciácie, a preto musíte s istotou využívať znalosti operácií so zlomkami;
• na zjednodušenie výrazu takmer vždy potrebujete vedieť trigonometrické identity, napríklad vzorec dvojitého uhla a vzorec jednotky ako súčet druhých mocnín sínusu a kosínusu.

Príklad 1 Nájdite deriváciu funkcie

Riešenie. Povedzme s derivát kosínusu všetko je jasné, povedia mnohí, ktorí začínajú študovať deriváty. Čo takto derivát sínusu dvanásť delené pí? Odpoveď: považujte to za rovné nule! Tu je sínus (koniec koncov funkcia!) pascou, pretože argumentom nie je premenná X ani iná premenná, ale iba číslo. To znamená, že sínus tohto čísla je tiež číslo. A derivácia čísla (konštanta), ako vieme z tabuľky derivácií, sa rovná nule. Takže ponecháme iba mínus sínus X a nájdeme jeho deriváciu, pričom nezabudneme na znamienko:

.

Príklad 2 Nájdite deriváciu funkcie

.

Riešenie. Druhý výraz je rovnaký prípad ako prvý výraz v predchádzajúcom príklade. To znamená, že je to číslo a derivácia čísla je nula. Deriváciu druhého člena nájdeme ako deriváciu kvocientu:

Príklad 3 Nájdite deriváciu funkcie

Riešenie. Toto je ďalší problém: tu v prvom člene nie je arksínus alebo iná trigonometická funkcia, ale je tam x, čo znamená, že je funkciou x. Preto ho rozlišujeme ako termín v súčte funkcií:

Tu boli potrebné zručnosti v operáciách so zlomkami, konkrétne pri odstraňovaní trojposchodovej štruktúry zlomku.

Príklad 4. Nájdite deriváciu funkcie

.

Riešenie. Písmeno "phi" tu hrá rovnakú úlohu ako "x" v predchádzajúcich prípadoch (a vo väčšine ostatných, ale nie vo všetkých) - nezávislá premenná. Preto, keď hľadáme deriváciu súčinu funkcií, nebudeme sa ponáhľať deklarovať deriváciu odmocniny „phi“ rovnú nule. Takže:

Tým sa ale riešenie nekončí. Keďže podobné výrazy sú zhromaždené v dvoch zátvorkách, stále sa od nás vyžaduje transformácia (zjednodušenie) výrazu. Preto zátvorky vynásobíme faktormi, ktoré sa za nimi stoja, a potom privedieme výrazy do spoločného menovateľa a vykonáme ďalšie elementárne transformácie:

Príklad 5. Nájdite deriváciu funkcie

Riešenie. V tomto príklade budeme potrebovať poznať skutočnosť, že existuje taká goniometrická funkcia – sečna – a jej vzorce cez kosínus. Poďme rozlišovať:

Príklad 6. Nájdite deriváciu funkcie

.

Riešenie. V tomto príklade si budeme musieť zapamätať vzorec dvojitého uhla zo školy. Najprv však rozlišujme:

,

(toto je vzorec dvojitého uhla)