Изследователски проект „Формулата на пика в геометрията на карираната хартия. Формулата на пика в училищния курс по планиметрия

Текстът на творбата е поставен без изображения и формули.
Пълната версия на произведението е достъпна в раздела "Работни файлове" в PDF формат

Въведение

Аз съм ученичка в 6 клас. Започнах да уча геометрия от миналата година, защото уча в училище по учебника „Математика. Аритметика. Геометрия "под редакцията на Ye.A. Бунимович, Л. В. Кузнецова, С. С. Минаева и др.

Най-много вниманието ми привлечеха темите „Квадрати от фигури“, „Съставяне на формули“. Забелязах, че областите с еднакви форми могат да бъдат намерени по различни начини. В ежедневието често сме изправени пред задачите да намерим зона. Например, намерете площта на пода, която ще боядисате. Любопитно е, в крайна сметка, за да закупите необходимото количество тапети за ремонт, трябва да знаете размера на стаята, т.е. площ на стената. Изчисляването на площта на квадрат, правоъгълник и правоъгълен триъгълник беше лесно за мен.

След като се заинтересувах от тази тема, започнах да търся допълнителен материал в Интернет. В резултат на моите търсения попаднах на формулата на Пик - това е формула за изчисляване на площта на многоъгълник, начертан върху карирана хартия. Изчисляването на площта по тази формула ми се стори достъпно за всеки ученик. Ето защо реших да се занимавам с изследователска работа.

Уместност на темата:

Тази тема е допълнение и задълбочаване на изучаването на курса по геометрия.

Изучаването на тази тема ще ви помогне да се подготвите по-добре за олимпиади и изпити.

Обективен:

Вижте формулата на Пик.

Овладейте техниките за решаване на геометрични задачи с помощта на формулата за избор.

Да систематизира и обобщи теоретични и практически материали.

Цели на изследването:

Проверете ефективността и осъществимостта на използването на формулата при решаване на проблеми.

Научете се да прилагате формулата на Пик в задачи с различна сложност.

Сравнете проблемите, решени с помощта на формулата за избор и традиционния метод.

Главна част

1.1. Справка по история

Георг Александър Пик е австрийски математик, роден на 10 август 1859 г. Той беше надарено дете, обучаван от баща си, който ръководеше частен институт. На 16-годишна възраст Георг завършва гимназия и постъпва във Виенския университет. На 20-годишна възраст получава правото да преподава физика и математика. Формулата за определяне на площта на решетка от многоъгълници му донесе световна слава. Той публикува формулата си в статия през 1899 г. Той става популярен, когато полският учен Хуго Щайнхаус го включва през 1969 г. в публикацията на математически снимки.

Георг Пик получава образование във Виенския университет и защитава докторска степен през 1880 г. След завършване на докторската си степен той е назначен за асистент на Ернест Мах в университета Шерл-Фердинанд в Прага. Там става и учител. Остава в Прага до пенсионирането си през 1927 г. и след това се връща във Виена.

Пик председателства комисия в Германския университет в Прага, която назначава Айнщайн за професор в катедрата по математическа физика през 1911 г.

Избран е за член на Чешката академия на изкуствата и науките, но е изключен след превземането на Прага от нацистите.

Когато нацистите влизат в Австрия на 12 март 1938 г., той се връща в Прага. През март 1939 г. нацистите нахлуват в Чехословакия. На 13 юли 1942 г. Пийк е депортиран в лагера Терезиенщат, създаден от нацистите в Северна Бохемия, където умира две седмици по-късно на 82-годишна възраст.

1.2. Изследване и доказателство

Започнах изследователската си работа, като изясних въпроса: областите на какви фигури мога да намеря? Бих могъл да измисля формула за изчисляване на площта на различни триъгълници и четириъгълници. Но какво да кажем за пет, шест и изобщо с многоъгълници?

В хода на проучване на различни сайтове видях решения на задачи за изчисляване на площта на пет, шест и други многоъгълници. Формулата за решаване на тези проблеми се нарича формула на Пик. Тя изглежда така: С = B + G / 2-1, където V- броят на възлите, разположени вътре в многоъгълника, г- броят на възлите, разположени на границата на многоъгълника. Особеността на тази формула е, че може да се използва само за многоъгълници, начертани върху карирана хартия.

Всеки такъв многоъгълник може лесно да бъде разделен на триъгълници с върхове в възлите на решетката, които не съдържат възли нито вътре, нито отстрани. Може да се покаже, че площите на всички тези триъгълници са еднакви и равни на ½ и следователно площта на многоъгълника е половината от техния брой Т.

За да намерим това число, означаваме с n броя на страните на многоъгълника с V- броят на възлите вътре в него, през г- броят на възлите от страните, включително върховете. Общата сума на ъглите на всички триъгълници е 180 °. Т.

Сега нека намерим сумата по различен начин.

Сумата от ъглите с върха във всеки вътрешен възел е 2,180 °, т.е. общата сума на ъглите е 360°. V;общата сума на ъглите при възлите отстрани, но не и във върховете, е ( G- n) 180°, а сумата от ъглите във върховете на многоъгълника ще бъде ( G-2) 180°. По този начин, T = 2,180°. B + (G-n) 180° + (н -2)180 °. След разширяване на скобите и разделяне на 360 °, получаваме формула за площта S на многоъгълник, известна като формула на Пик.

2. Практическа част

Реших да проверя тази формула на задачи от колекцията OGE-2017. Взех задачи за изчисляване на площта на триъгълник, четириъгълник и петоъгълник. Реших да сравня отговорите, решавайки по два начина: 1) добавих фигурите към правоъгълника и от площта на получения правоъгълник извадих площта на правоъгълните триъгълници; 2) прилага формулата на Пик.

S = 18-1,5-4,5 = 12 и S = 7 + 12 / 2-1 = 12

S = 24-9-3 = 12 и S = 7 + 12 / 2-1 = 12

S = 77-7,5-12-4,5-4 = 49 и S = 43 + 14 / 2-1 = 49

Сравнявайки полученото, заключавам, че и двете формули дават един и същ отговор. Намирането на площта на фигура с помощта на формулата Peak се оказа по-бързо и по-лесно, тъй като имаше по-малко изчисления. Лесното решение и спестяването на време за изчисления ще ми бъдат полезни в бъдеще при преминаване на OGE.

Това ме подтикна да тествам възможността за прилагане на формулата на Пик върху по-сложни форми.

S = 0 + 4/2 -1 = 1

S = 5 + 11 / 2-1 = 9,5

S = 4 + 16 / 2-1 = 1

Заключение

Формулата на Peak е лесна за разбиране и лесна за използване. Първо, достатъчно е да можете да броите, да разделите на 2, да събирате и изваждате. Второ, можете да намерите площ и сложна форма, без да харчите много време. Трето, тази формула работи за всеки многоъгълник.

Недостатъкът е, че Pick Formula е приложима само за фигури, които са нарисувани върху карирана хартия и върховете лежат във възлите на клетките.

Сигурен съм, че при полагане на финалните изпити проблемите с изчисляването на площта на фигурите няма да предизвикат трудности. В крайна сметка вече съм запознат с формулата на Пик.

Библиография

Бунимович Е.А., Дорофеев Г.В., Суворова С.Б. и друга математика. Аритметика. Геометрия. 5 клас: образователен. за общо образование. организации с прил. към електрона. носител-3-то изд.-М .: Образование, 2014.- 223, с. : аз ще. - (сфери).

Бунимович Е.А., Кузнецова Л.В., Минаева С.С. и друга математика. Аритметика. Геометрия. 6 клас: образователен. за общо образование. организации-5-то изд.-М .: Образование, 2016.-240с. : ил. - (Сфери).

Василиев Н.Б. Около формулата на Пик. // Количество - 1974.-№2. -с. 39-43

Рассолов В.В. Задачи по планиметрия. / 5-то изд., Rev. И добавете. - М .: 2006.-640-те.

И.В. Яшченко, OGE. Математика: типични изпитни варианти: О-39 36 варианта - М .: Издателство Национално образование, 2017. -240 с. - (ОГЕ. ФИПИ-училище).

„Ще реша OGE“: математика. Системата за обучение на Дмитрий Гущин. OGE-2017: задачи, отговори, решения [Електронен ресурс]. Режим на достъп: https://oge.sdamgia.ru/test?id=6846966 (дата на лечението 02.04.2017 г.)

Използвайки формулата за избор, можете да намерите площта на фигура, изградена върху лист в клетка (триъгълник, квадрат, трапец, правоъгълник, многоъгълник).

В задачите, които ще бъдат на изпита, има цяла група задачи, в които е даден многоъгълник, изграден върху лист в клетка и въпросът е за намиране на площта. Мащабът на клетката е един квадратен сантиметър.

Преглед на съдържанието на презентацията

Връх Георг

връх Георг Александър,

австрийски математик

(10.08.1859 - 13.07.1942)

Формулата е открита през 1899 г.

Площта на необходимата фигура може да се намери по формулата:

M е броят на възлите на границата на триъгълника (отстрани и върхове):
N е броят на възлите в триъгълника;

* Под "възли" имаме предвид пресечната точка на линиите.

Нека намерим площта на триъгълника:

Нека отбележим възлите:

1 клетка = 1 см

M = 15 (маркирани в червено)
N = 34 (маркирани в синьо)

Намерете площта на паралелограма:

Нека отбележим възлите:

M = 18 (маркирани в червено)
N = 20 (маркирани в синьо)

Нека намерим площта на трапеца:

Нека отбележим възлите:

M = 24 (маркирани в червено)
N = 25 (маркирани в синьо)

Намерете площта на многоъгълника:

Нека отбележим възлите:

M = 14 (маркирани в червено)
N = 43 (маркирани в синьо)

Нека отбележим възлите:

M = 11 (маркирани в червено)
N = 5 (маркирани в синьо)

Решете сами:

1. Намерете площта на четириъгълник, изобразен върху карирана хартия с размер на клетката 1 см х 1 см. Дайте отговора си в квадратни сантиметри.

4. Намерете площта на четириъгълник, изобразен върху карирана хартия с размер на клетка 1 см х 1 см. Дайте отговора си в квадратни сантиметри .

Нека опишем правоъгълник близо до него:

От площта на правоъгълника (в този случай това е квадрат) изваждаме площите на получените прости фигури:

Отговори:

№ задачи

Опция 1

Вариант 2

Вариант 3

Вариант 4

Пикова формула

Сажина Валерия Андреевна, ученик от 9 клас, MAOU "Средно училище № 11" Уст-Илимск, Иркутска област

Ръководител: Губар Оксана Михайловна, учител по математика от най-висока квалификационна категория MAOU "Средно училище № 11" Уст-Илимск, Иркутска област

2016 година

Въведение

Докато изучавах темата по геометрия "Площи на многоъгълници", реших да разбера: има ли начин да се намерят области, различни от тези, които изучавахме в уроците?

Този начин е формулата на Пик. Л. В. Горина в „Материали за самообучение на учениците” описва тази формула по следния начин: „Опознаването на формулата на Пик е особено важно в навечерието на ЕГЭ и Агенцията за държавни изпити. Използвайки тази формула, можете лесно да решите голям клас задачи, предлагани в изпитите - това са проблеми за намиране на площта на многоъгълник, изобразен върху карирана хартия. Малката формула на Пик ще замени целия набор от формули, необходими за решаване на подобни проблеми. Формулата на Pick ще работи „един за всички...“!“.

В материалите на изпита срещнах проблеми с практическото съдържание при намиране на площта на парцелите. Реших да проверя дали тази формула е приложима, за да намеря площта на територията на училището, градските микрорайони и района. И също така рационално ли е да се използва за решаване на проблеми.

Обект на изследване: Формулата на Пик.

Предмет на изследване: рационалността на прилагането на формулата на Пик при решаване на задачи.

Цел на работата: да се обоснове рационалността на използването на формулата за избор при решаване на задачи за намиране на площта на фигурите, изобразени върху карирана хартия.

Методи на изследване: моделиране, сравнение, обобщение, аналогии, изследване на литературни и интернет ресурси, анализ и класификация на информацията.

Изберете необходимата литература, анализирайте и систематизирайте получената информация;

Разгледайте различни методи и техники за решаване на задачи върху карирана хартия;

Експериментално проверете рационалността на използването на формулата за избор;

Помислете за прилагането на тази формула.

Хипотеза: ако приложите формулата на пика, за да намерите площите на многоъгълник, тогава можете да намерите площта на територията и решаването на проблеми на карирана хартия ще бъде по-рационално.

Главна част

Теоретична част

Карираната хартия (по-точно нейните възли), върху която често предпочитаме да рисуваме и рисуваме, е един от най-важните примери за пунктирана решетка на равнина. Тази проста решетка вече послужи като отправна точка за К. Гаус за сравняване на площта на кръг с броя на точките с цели координати, разположени вътре в него. Фактът, че някои прости геометрични твърдения за фигури на равнина имат дълбоки последствия в аритметичните изследвания, е изрично отбелязан от Г. Минковски през 1896 г., когато за първи път използва геометрични методи за разглеждане на теоретически проблеми на числата.

Нека начертаем многоъгълник върху карирана хартия (Приложение 1, Фигура 1). Нека сега се опитаме да изчислим неговата площ. Как да го направя? Може би най-лесният начин е да го разделите на правоъгълни триъгълници и трапец, чиито площи вече са лесни за изчисляване и сумиране на резултатите.

Използваният метод е прост, но много тромав, освен това не е подходящ за всички полигони. Така че следващият многоъгълник не може да бъде разделен на правоъгълни триъгълници, както направихме в предишния случай (Приложение 2, Фигура 2). Можете например да се опитате да го допълните с "добрия", който ни е необходим, тоест към този, който можем да изчислим площта, на която можем да изчислим по описания начин, след което да извадим площите на добавеното части от полученото число.

Оказва се обаче, че има много проста формула, която ви позволява да изчислите площите на такива многоъгълници с върхове в възлите на квадратна мрежа.

Тази формула е открита от австрийския математик Пик Георг Александров (1859 - 1943) през 1899 г. В допълнение към тази формула, Георг Пик открива теоремите на Пик, Пик – Юлия, Пик – Невалина и доказва неравенството на Шварц – Пик.

Тази формула остава незабелязана известно време, след като Пийк я публикува, но през 1949 г. полският математик Хуго Щайнхаус включва теоремата в известния си математически калейдоскоп. От това време нататък теоремата на Пик става широко известна. В Германия формулата на Пик е включена в училищните учебници.

Това е класическият резултат от комбинаторната геометрия и геометрията на числата.

Доказателство за формулата на Пик

Нека ABCD е правоъгълник с върхове във възлите и страните по линиите на мрежата (Приложение 3, Фигура 3).

Нека означим с В - броят на възлите, разположени вътре в правоъгълника, а с Г - броят на възлите на неговата граница. Преместете решетката половин клетка надясно и половин клетка

надолу. Тогава територията на правоъгълника може да бъде "разпределена" между възлите по следния начин: всеки от B възлите "контролира" цялата клетка на изместената мрежа, а всеки от възлите G - 4 гранични неъглови възела - половин клетка , а всяка от ъгловите точки - една четвърт от клетка. Следователно площта на правоъгълника S е равна на

С = B + + 4 = B + - 1 .

И така, за правоъгълници с върхове във възлите и страните, минаващи по линиите на мрежата, задаваме формулата S = B + - 1 . Това е формулата на Пик.

Оказва се, че тази формула е вярна не само за правоъгълници, но и за произволни многоъгълници с върхове в възлите на мрежата.

Практическа част

Намиране на площта на фигурите по геометричния метод и по формулата за избор

Реших да се уверя, че формулата на Пик е правилна за всички примери, които разгледах.

Оказва се, че ако един многоъгълник може да бъде нарязан на триъгълници с върхове в възлите на мрежата, тогава формулата на Пик е вярна за него.

Прегледах някои задачи върху карирана хартия с клетки с размери 1 cm1 cm и направих сравнителен анализ за решаване на задачи (Таблица 1).

Таблица №1 Решаване на задачи по различни начини.

Рисуване

По геометрична формула

По формулата на Пика

Проблем номер 1

S = Sи т.н - (2S 1 + 2S 2 )

Си т.н =4*5=20 см 2

С 1 =(2*1)/2=1 см 2

С 2 =(2*4)/2=4 см 2

S = 20- (2 * 1 + 2 * 4) = 10см 2

Отговор :10 см ².

B = 8, G = 6

С= 8 + 6/2 - 1 = 10 (см²)

Отговор: 10 см².

Проблем номер 2

а = 2, з = 4

S = a * h = 2 * 4 = 8см 2

Отговор : 8 см ².

B = 6, G = 6

С= 6 + 6/2 - 1 = 8 (см²)

Отговор: 8 см².

Проблем номер 3

S = Sкв. - (С 1 + 2S 2 )

Скв. =4 2 =16 см 2

С 1 = (3 * 3) / 2 = 4,5 см 2

С 2 = (1 * 4) / 2 = 2 см 2

С= 16- (4,5 + 2 * 2) = 7,5 см 2

B = 6, G = 5

С= 6 + 5/2 - 1 = 7,5 (см²)

Отговор: 7,5 см².

Проблем номер 4

S = Sи т.н - (С 1 + С 2+ С 3 )

Си т.н =4 * 3=12 см 2

С 1 =(3*1)/2=1,5 см 2

С 2 =(1*2)/2=1 см 2

С 3 =(1+3)*1/2=2 см 2

S = 12- (1,5 + 1 + 2) = 7,5см 2

B = 5, G = 7

С= 5 + 7/2 - 1 = 7,5 (см²)

Отговор: 7,5 см².

Проблем № 5.

S = Sи т.н - (С 1 + С 2+ С 3 )

Си т.н =6 * 5=30 см 2

С 1 =(2*5)/2=5 см 2

С 2 =(1*6)/2=3 см 2

С 3 =(4*4)/2=8 см 2

S = 30- (5 + 3 + 8) = 14см 2

Отговор: 14 см²

Н = 12, G = 6

С= 12 + 6/2 - 1 = 14 (см²)

Отговор: 14 см²

Задача №6.

С tr = (4 + 9) / 2 * 3 = 19,5 cm 2

Отговор: 19,5 см 2

Н = 12, G = 17

С= 12 + 17/2 - 1 = 19,5 (см²)

Отговор: 19,5 см 2

Задача №7. Намерете площта на гората (в m²), показана на плана с квадратна решетка 1 × 1 (cm) в мащаб от 1 cm - 200 m

S = S 1 + С 2+ С 3

С 1 =(800*200)/2=80000 м 2

С 2 =(200*600)/2=60000 м 2

С 3 =(800+600)/2*400=

280000 м 2

S = 80000+60000+240000=

420 000 м 2

Отговор: 420 000 m²

B = 8, G = 7. С= 8 + 7/2 - 1 = 10,5 (см²)

1 cm² - 200² m²; С= 40 000 10,5 = 420 000 (m2)

Отговор: 420 000 m²

Проблем номер 8 ... Намерете площта на полето (в m²), изобразена на плана с квадратна мрежа 1 × 1 (см) в мащаб

1 см - 200 м.

С= Скв. -2 ( С tr + Сстълба)

Скв. = 800 * 800 = 640 000 m 2

С tr = (200 * 600) / 2 = 60 000 m 2

Сстълба = (200 + 800) / 2 * 200 =

100 000 м 2

С=640000-2(60000+10000)=

320 000 m 2

Отговор: 320 000 m²

Решение.намирам Сплощта на четириъгълник, изобразен върху карирана хартия с помощта на формулата на Пик:С= B + - 1

B = 7, G = 4. С= 7 + 4/2 - 1 = 8 (см²)

1 cm² - 200² m²; С= 40 000 8 = 320 000 (m2)

Отговор: 320 000 m²

Проблем номер 9 ... Намерете районаС сектор, като се имат предвид страните на квадратни клетки, равни на 1. Във вашия отговор посочете .

Секторът е една четвърт от кръга и следователно неговата площ е равна на една четвърт от площта на кръг. Площта на кръг е πР 2 , където Р Радиусът на окръжността. В нашия случайР =√5 и следователно площтаС секторът е 5π / 4. КъдетоС/ π = 1,25.

Отговор. 1.25.

G = 5, B = 2, С= B + G / 2 - 1 = 2 + 5/2 - 1 = 3,5, ≈ 1,11

Отговор. 1.11.

Проблем номер 10. Намерете района С пръстени, като се броят страните на квадратни клетки, равни на 1. Във вашия отговор посочете .

Площта на пръстена е равна на разликата между площите на външния и вътрешния кръг. РадиусР външният кръг е

2, радиус r вътрешният кръг е 2. Следователно площта на пръстена е 4и следователно... Отговор: 4.

G = 8, B = 8, С= B + G / 2 - 1 = 8 + 8/2 - 1 = 11, ≈ 3,5

Отговор: 3.5

Изводи: Разгледаните задачи са подобни на задачата от вариантите за контролно-измервателните материали на изпита по математика (задачи No 5,6).

От разгледаните решения на задачите видях, че някои от тях, например задачи № 2.6, са по-лесни за решаване с помощта на геометрични формули, тъй като височината и основата могат да се определят от снимката. Но в повечето задачи се изисква разделяне на фигурата на по-прости (задача № 7) или завършване на конструкцията до правоъгълник (задачи № 1,4,5), квадрат (задачи № 3,8).

От решаването на задачи № 9 и № 10 видях, че прилагането на формулата на Пик към форми, които не са многоъгълници, дава приблизителен резултат.

За да проверя рационалността на формулата на Пик, проведох проучване по темата за прекараното време (Приложение 4, таблица №2).

Заключение: от таблицата и диаграмата (Приложение 4, диаграма 1) се вижда, че при решаване на проблеми с помощта на формулата на Пик се изразходва много по-малко време.

Намиране на повърхността на пространствените форми

Нека проверим приложимостта на тази формула към пространствените форми (Приложение 5, Фигура 4).

Намерете общата повърхност на правоъгълен паралелепипед, като приемете, че страните на квадратните клетки са 1.

Това е недостатък във формулата.

Прилагане на формулата на пика за намиране на площта на територията

Решавайки проблеми с практическо съдържание (задачи № 7,8; таблица № 1), реших да приложа този метод, за да намеря района на територията на нашето училище, микрорайони на град Уст-Илимск , Иркутска област.

След преглед на „Проекта за границите на поземлен имот MAUSOSH № 11 в Уст-Илимск“ (Приложение 6), намерих площта на територията на нашето училище и я сравних с площта според проекта на границите на парцела (Приложение 9, таблица 3).

След като разгледах картата на дясната част на Усть-Илимск (Приложение 7), изчислих площите на микрорайоните и ги сравних с данните от „Генералния план на Усть-Илимск, Иркутска област“. Резултатите са представени в таблицата (Приложение 9, таблица 4).

След като разгледах картата на Иркутска област (Приложение 7), намерих площта на територията и я сравних с данните от Уикипедия. Резултатите са представени в таблицата (Приложение 9, таблица 5).

След като анализирах резултатите, стигнах до заключението: с помощта на формулата Peak тези области могат да бъдат намерени много по-лесно, но резултатите са приблизителни.

От проведеното изследване получих най-точната стойност при намиране на площта на училищната територия (Приложение 10, диаграма 2). По-голямо несъответствие в резултатите се получава при намиране на района на Иркутска област (Приложение 10, диаграма 3). Това се дължи на факта. Че не всички граници на области са страни на многоъгълници, а върховете не са опорни точки.

Заключение

В резултат на моята работа разширих познанията си за решаване на задачи върху карирана хартия, определих за себе си класификацията на изучаваните задачи.

При извършване на работата бяха решени проблемите за намиране на площта на многоъгълниците, изобразени върху карирана хартия, по два начина: геометричен и с помощта на формулата за избор.

Анализът на решенията и експериментът за определяне на изразходваното време показаха, че прилагането на формулата дава възможност за решаване на задачи за намиране на площта на многоъгълник по по-рационален начин. Това спестява време на изпита по математика.

Намирането на площта на различни фигури, изобразени върху карирана хартия, даде възможност да се заключи, че използването на формулата на Пик за изчисляване на площта на кръгов сектор и пръстен е непрактично, тъй като дава приблизителен резултат и че формулата на Пик не се използва за решаване на проблеми в космоса.

Също така, в работата, площите на различни територии са открити с помощта на формулата Peak. Можем да заключим, че използването на формулата за намиране на площта на различни територии е възможно, но резултатите са приблизителни.

Изложената от мен хипотеза се потвърди.

Стигнах до извода, че темата, която ме интересува е доста многостранна, задачите на карирана хартия са разнообразни, разнообразни са и методите и техниките за тяхното решаване. Затова реших да продължа да работя в тази посока.

литература

Волков С.Д.. Проект за граници на парцела, 2008 г., с. шестнадесет.

Горина Л.В., Математика. Всичко за учителя, М: Наука, 2013, No 3, с. 28.

Прокопьева В.П., Петров А.Г., Генерален план на град Усть-Илимск, Иркутска област, Госстрой на Русия, 2004 г., стр. 65

Рис Е.А., Жарковская Н.М., Геометрия на карирана хартия. Формула на Пик. - Москва, 2009, № 17, с. 24-25.

Смирнова И. М.,. Смирнов В. А., Геометрия върху карирана хартия. - Москва, Чистые пруды, 2009, с. 120.

Смирнова И.М., Смирнов В.А., Геометрични задачи с практическо съдържание. - Москва, Чистые пруды, 2010, с. 150

Проблеми на отворената банка от задачи по математика на FIPI, 2015 г.

Карта на град Уст-Илимск.

Карта на Иркутска област.

Уикипедия.

Пикова формула

1. Въведение

2. Формула на Пик. Доказателство за И.

Доказателство II.

Доказателството на Ш.

3. Задачи.

4. Формула за площта на многоъгълник през координатите на върховете.

5. Задачи.

6. Литература

Формула на Пик.

1. Въведение.

Ние черпим мъдрост от историята,

в поезията - остроумие,

в математиката, проницателност.

Ф. Бекон

Сюжетът ще се разгърне върху обикновена карирана хартия.

Линиите, минаващи по страните на клетките, образуват мрежа, а върховете на клетките образуват възлите на тази мрежа. Нека начертаем многоъгълник на листа с върхове във възлите и да намерим неговата площ.

Можете да го търсите по различни начини. Например, можете да изрежете многоъгълник в доста прости форми, да намерите техните области и да ги сгънете.

Но тук ни чакат много неприятности. Една фигура може лесно да бъде разбита на правоъгълници, трапеци и триъгълници, а нейната площ се изчислява без усилие.

Въпреки че многоъгълникът изглежда достатъчно прост, изчисляването на неговата площ ще отнеме много работа. Ами ако многоъгълникът изглеждаше по-странен? Оказва се, че площите на многоъгълници, чиито върхове са разположени в възлите на мрежата, могат да бъдат изчислени много по-лесно: има формула, която свързва тяхната площ с броя на възлите, лежащи вътре и на границата на многоъгълника. Тази прекрасна и проста формула се нарича формула на Пик.

2. Формула на Пик.

Върховете на многоъгълник (не непременно изпъкнали) са разположени в възлите на целочислена решетка. Вътре в него се намира B възли на решетката, а на границата Γ на възли. Нека докажем, че неговата площ е равна на B + - 1 (Формула на Пик).

Доказателство за И.

Помислете за многоъгълник, чиито върхове са в възлите на целочислена решетка, тоест имат целочислени координати.

Разделете многоъгълника на триъгълници с върхове в възлите на решетката, които не съдържат възли нито вътре, нито отстрани.

Да обозначим:

н- броят на страните на многоъгълника,

м- броят на триъгълниците с върхове във възлите на решетката, които не съдържат възли нито вътре, нито отстрани,

B - броят на възлите вътре в многоъгълника,

Г е броят на възлите от страните, включително върховете.

Площите на всички тези триъгълници са еднакви и равни.

Следователно площта на многоъгълника е
.

180 0 м .

Сега нека намерим тази сума по различен начин.

Сумата от ъглите с върха във всеки вътрешен възел е 360 0.

Тогава сумата от ъглите с върховете във всички вътрешни възли е 360 0 V.

Общата сума на ъглите при възлите отстрани, но не и във върховете е равна на 180 0 (Г - н).

Сумата от ъглите при върховете на многоъгълника е 180 0 ( н – 2) .

Общата сума от ъглите на всички триъгълници е 360 0 V + 180 0 (G - н) + 180 0 (н – 2).

Така 180 0 м= 360 0 V + 180 0 (G - н) + 180 0 (н – 2),

180 0 м= 360 0 V + 180 0 G - 180 0 н + 180 0 н- 180 0 2,

180 0 м= 360 0 V + 180 0 G - 360 0,

= B + – 1 ,

откъдето получаваме израза за площта S на многоъгълника:

С= B + – 1 ,

известна като формула на Пик.

На фигурата: H = 24, G = 9, следователно,С = 24 + – 1 = 27,5.

Намерете площта на първия многоъгълник, като използвате формулата за избор:

B = 28 (зелени точки);

G = 20 (сини точки).

Получаваме, S =
= 37 кв. единици

Доказателство II.

На всеки многоъгълник M с върхове в възлите на целочислената решетка приписваме числото f (M) =
, където сумирането се извършва върху всички възли на решетката, принадлежащи на M, и ъгъла се определя, както следва: =
за вътрешната точка на многоъгълника, =
за гранична точка, различна от връх, и - ъгълът при върха, ако даденият възел е връх. Лесно е да се види, че f (M) =
+
= B + - 1. Остава да проверим дали числото f (M) е равно на площта на многоъгълника M.

Нека многоъгълникът M бъде нарязан на многоъгълници M 1 и M 2 с върхове във възлите на решетката. Тогава f (M) = f (M 1) + f (M 2), тъй като ъглите се сумират за всеки възел. Следователно, ако формулата на Пик е вярна за два от многоъгълниците M, M 1 и M 2, тогава тя е вярна и за третия.

Ако M е правоъгълник със страни стри qнасочени по решетъчните линии, тогава

f (M) = (p - 1) (q - 1) +
= pq.

В този случай формулата на Пик е валидна. Изрязването на правоъгълник M с диагонал на триъгълници M 1 и M 2 и използване на факта, че f (M) = f (M 1) + f (M 2) и f (M 1) = f (M 2), е лесно за да докаже формулата на Pick за всеки правоъгълен триъгълник с катета, насочени по протежение на решетъчните линии. Като отрежете няколко от тези триъгълници от правоъгълник, можете да получите всеки триъгълник.

За да завършим доказателството на формулата на Пик, остава да отбележим, че всеки многоъгълник може да бъде нарязан на триъгълници чрез непреходни диагонали.

Доказателството на Ш.

Връзката между площта на фигура и броя на възлите, които попадат в тази форма, е особено ясна в случай на правоъгълник.

Позволявам ABCD- правоъгълник с върхове във възлите и страните по линиите на мрежата.

Нека означим с Vброят на възлите, лежащи вътре в правоъгълника, и след това г- броят на възлите на границата му. Преместете решетката с половин клетка надясно и с половин клетка надолу.

Тогава територията на правоъгълника може да бъде "разпределена" между възлите, както следва: всеки от Vвъзли "контролира" цялата клетка на изместената мрежа, всяка от г- 4 гранични неъглови възела - половин клетка, и всяка от ъгловите точки - една четвърт клетка. Следователно площта на правоъгълника S е равна на

И така, за правоъгълници с върхове във възлите и страните, минаващи по линиите на мрежата, задаваме формулата

Нека докажем, че тази формула е валидна не само за правоъгълници, но и за произволни многоъгълници с върхове в възлите на мрежата.

Нека означим с С м полигонна площМ с върхове във възлите и презП м - стойност
, къдетоV м - брой възли вътреМ,а г м - броят на възлите на границата. Тогава формулата на Пик може да се запише като
.

Разделяме доказателството на формулата на няколко стъпки.

Етап 1.

Ако многоъгълникътМ с върхове в точките на мрежата се нарязва на 2 многоъгълникаМ 1 и М 2 , също има върхове само в възлите на мрежата, тогава
... Нека многоъгълникътМ нарязани на многоъгълнициМ 1 и М 2 с върхове във възли по сегментАБ. Всички възли, с изключение на тези, които попадат в сегментаAB, дават еднакъв принос към лявата и дясната част на формулата. Да разгледаме възлите, лежащи на отсечката AB.

Ако такъв възел лежи между A и B (например C), тогава за многоъгълникМ той е вътрешен, но за многоъгълнициМ 1 и М 2 - граница. Следователно неговият принос къмП м е равно на 1 и във всеки от изразите
и
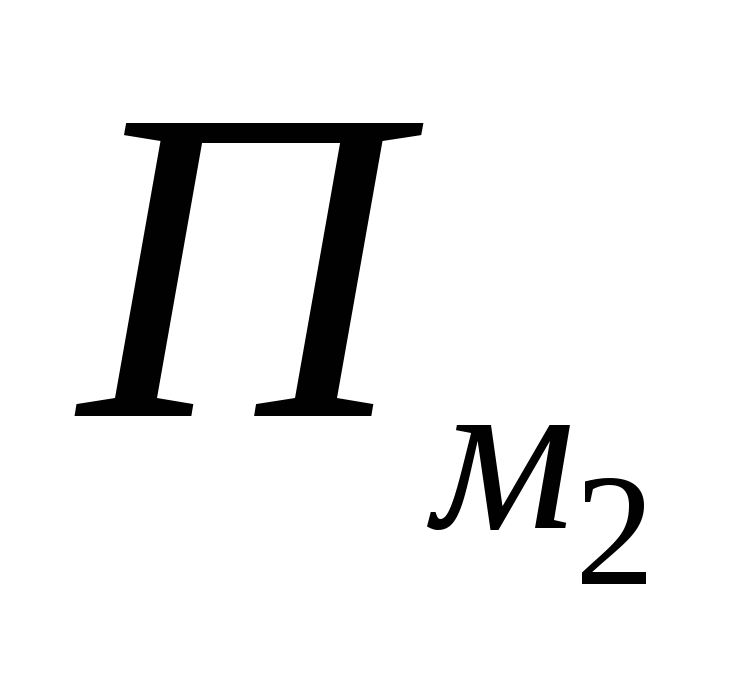- 0,5 всеки, тоест приносите на такъв възел къмП м и
са равни.

Помислете за възли A и B. Те са гранични като за Ми за М 1 , М 2 .

Следователно приносът на всеки от тези възли къмП м е равно на 0,5 a in
- мерна единица. Следователно общият принос на възлите A и B къмП м е равно на 1, което е с 1 по-малко от техния принос към
. Но
, а .

От общия "принос" на всички възли П мизважда 1 и от
извадете 2 и това компенсира разликата в приноса на възлите A и B.

Така,
.

Стъпка 2.

Ако многоъгълникът Мс върхове в точките на окото се разрязва на два многоъгълника М 1 и М 2 (също с върхове във възлите) и формулата е правилна за някои два от многоъгълниците ММ 1 , М 2 , то е вярно и за третия многоъгълник.

Например, нека е вярно заМ 1 и М 2 , това е
... След това (според първата стъпка), но на първа стъпка) последният израз еП м , и равенство
и има формулата на Пийк.

Стъпка 3.

Нека докажем формулата на Pick за правоъгълен триъгълник с върхове във възлите на мрежата и катета, лежащи върху линиите на мрежата.

триъгълник ABCпостроете до правоъгълника ABCD .

За правоъгълници формулата на Пик е правилна: С ABCD = П ABCD . Според първата стъпка П ABCD = П ABC + П ACD , П ABC = П ACD , така П ABCD = 2P ABC . Но С ABCD = 2 С ABC ... Така С ABC = П ABC .

Стъпка 4.

Формулата на Пик е правилна за произволен триъгълник с върхове в точките на мрежата.

След като разгледахме фигурата, е лесно да се разбере: всеки такъв триъгълник може да бъде получен чрез "отрязване" от някакъв правоъгълник със страни, минаващи по линиите на мрежата, няколко правоъгълника и правоъгълни триъгълници с крака върху линиите на мрежата. И тъй като формулата на Пик е вярна за правоъгълници и правоъгълни триъгълници, тогава (припомнете си стъпка 2) тя е вярна и за оригиналния триъгълник.

Доказахме, че ако един многоъгълник може да бъде нарязан на триъгълници с върхове във възлите на мрежата, тогава формулата на Пик е вярна за него.

3. Задачи.

Намерете областите на фигурите:

1
.