Výskumný projekt „Vzorec vrcholu v geometrii kockovaného papiera. Špičkový vzorec v školskom kurze planimetrie

Text práce je umiestnený bez obrázkov a vzorcov.
Plná verzia diela je dostupná v záložke „Súbory práce“ vo formáte PDF

Úvod

Som žiačkou 6. ročníka. Geometriu som začal študovať od minulého roka, pretože v škole študujem podľa učebnice „Matematika. Aritmetika. Geometria “upravil Ye.A. Bunimovič, L. V. Kuznecovová, S. S. Minaeva a ďalší.

Najviac ma zaujali témy „Štvorce obrazcov“, „Skladanie vzorcov“. Všimol som si, že oblasti rovnakých tvarov možno nájsť rôznymi spôsobmi. V každodennom živote sa často stretávame s úlohami nájsť oblasť. Napríklad nájdite plochu podlahy, ktorá sa má natrieť. Je to kuriózne, veď na to, aby ste si kúpili potrebné množstvo tapiet na renováciu, potrebujete poznať veľkosť miestnosti, t.j. oblasť steny. Výpočet plochy štvorca, obdĺžnika a pravouhlého trojuholníka bol pre mňa jednoduchý.

Keď som sa o túto tému začal zaujímať, začal som hľadať ďalší materiál na internete. V dôsledku môjho hľadania som narazil na Pickov vzorec - je to vzorec na výpočet plochy mnohouholníka nakreslený na kockovanom papieri. Výpočet plochy pomocou tohto vzorca sa mi zdal dostupný pre každého študenta. Preto som sa rozhodol pre výskumnú prácu.

Relevantnosť témy:

Táto téma je doplnením a prehĺbením štúdia kurzu geometrie.

Štúdium tejto témy vám pomôže lepšie sa pripraviť na olympiády a skúšky.

Účel práce:

Pozrite si Pickov vzorec.

Osvojte si techniky riešenia geometrických problémov pomocou Pickovho vzorca.

Systematizovať a zhrnúť teoretické a praktické materiály.

Ciele výskumu:

Skontrolujte efektívnosť a uskutočniteľnosť použitia vzorca pri riešení problémov.

Naučte sa používať vzorec Peak v problémoch rôznej zložitosti.

Porovnajte problémy vyriešené pomocou Pick vzorca a tradičnou metódou.

Hlavná časť

1.1. Historický odkaz

Georg Alexander Pick je rakúsky matematik, narodený 10. augusta 1859. Bol nadaným dieťaťom, učil ho jeho otec, ktorý viedol súkromný ústav. Ako 16-ročný Georg vyštudoval strednú školu a vstúpil na Viedenskú univerzitu. Vo veku 20 rokov získal právo vyučovať fyziku a matematiku. Vzorec na určenie plochy mriežky polygónov mu priniesol celosvetovú slávu. Svoj vzorec publikoval v článku v roku 1899. Populárnym sa stal, keď ho poľský vedec Hugo Steinhaus v roku 1969 zaradil do publikácie matematických fotografií.

Georg Pick získal vzdelanie na Viedenskej univerzite a v roku 1880 obhájil doktorát. Po ukončení doktorátu bol vymenovaný za asistenta Ernesta Macha na Sherl-Ferdinandovej univerzite v Prahe. Stal sa tam aj učiteľom. V Prahe zostal až do odchodu do dôchodku v roku 1927 a potom sa vrátil do Viedne.

Pick predsedal výboru na Nemeckej univerzite v Prahe, ktorý v roku 1911 vymenoval Einsteina za profesora na oddelení matematickej fyziky.

Bol zvolený za člena Českej akadémie umení a vied, no po nacistickom zajatí Prahy bol vylúčený.

Keď nacisti 12. marca 1938 vstúpili do Rakúska, vrátil sa do Prahy. V marci 1939 nacisti napadli Československo. 13. júla 1942 bol Peak deportovaný do tábora Theresienstadt, zriadeného nacistami v severných Čechách, kde o dva týždne neskôr vo veku 82 rokov zomrel.

1.2. Výskum a dôkaz

Svoju výskumnú prácu som začal objasnením otázky: oblasti akých čísel môžem nájsť? Mohol by som prísť so vzorcom na výpočet plochy rôznych trojuholníkov a štvoruholníkov. Ale čo päť, šesť a všeobecne s polygónmi?

V priebehu výskumu na rôznych miestach som videl riešenia problémov pre výpočet plochy piatich, šiestich a iných polygónov. Vzorec na riešenie týchto problémov sa nazýval Pickov vzorec. Vyzerá takto: S = B + G / 2-1, kde V- počet uzlov ležiacich vo vnútri polygónu, G- počet uzlov ležiacich na hranici mnohouholníka. Zvláštnosťou tohto vzorca je, že ho možno použiť len pre polygóny nakreslené na kockovanom papieri.

Každý takýto mnohouholník možno ľahko rozdeliť na trojuholníky s vrcholmi v uzloch mriežky, ktoré neobsahujú uzly ani vo vnútri, ani po stranách. Dá sa ukázať, že plochy všetkých týchto trojuholníkov sú rovnaké a rovné ½, a preto je plocha mnohouholníka polovica ich počtu. T.

Aby sme našli toto číslo, označíme n počet strán mnohouholníka, by V- počet uzlov vo vnútri, cez G- počet uzlov na stranách vrátane vrcholov. Celkový súčet uhlov všetkých trojuholníkov je 180°. T.

Teraz zistime sumu iným spôsobom.

Súčet uhlov s vrcholom v ktoromkoľvek vnútornom uzle je 2,180°, t.j. súčet uhlov je 360°. V; celkový súčet uhlov v uzloch na stranách, ale nie vo vrcholoch, je ( G-n) 180° a súčet uhlov vo vrcholoch mnohouholníka bude ( G-2) 180°. teda T = 2,180 °. B+ (G-n) 180° + (č -2)180 °. Po rozbalení zátvoriek a delení o 360° dostaneme vzorec pre oblasť S mnohouholníka, známy ako Pickov vzorec.

2. Praktická časť

Rozhodol som sa skontrolovať tento vzorec na úlohách z kolekcie OGE-2017. Zobral som si úlohy na výpočet plochy trojuholníka, štvoruholníka a päťuholníka. Rozhodol som sa porovnať odpovede a vyriešiť dvoma spôsobmi: 1) pridal som čísla do obdĺžnika a z plochy výsledného obdĺžnika som odpočítal plochu pravouhlých trojuholníkov; 2) aplikoval Pickov vzorec.

S = 18-1,5-4,5 = 12 a S = 7 + 12 / 2-1 = 12

S = 24-9-3 = 12 a S = 7 + 12 / 2-1 = 12

S = 77-7,5-12-4,5-4 = 49 a S = 43 + 14 / 2-1 = 49

Porovnaním prijatých som dospel k záveru, že oba vzorce dávajú rovnakú odpoveď. Nájdenie oblasti obrazca pomocou vzorca Peak sa ukázalo byť rýchlejšie a jednoduchšie, pretože bolo menej výpočtov. Jednoduchosť riešenia a úspora času pri výpočtoch sa mi bude hodiť v budúcnosti pri absolvovaní OGE.

To ma podnietilo otestovať možnosť aplikácie Pickovho vzorca na zložitejšie tvary.

S = 0 + 4/2-1 = 1

S = 5 + 11/2-1 = 9,5

S = 4 + 16/2-1 = 1

Záver

Peakov vzorec je ľahko pochopiteľný a ľahko použiteľný. Najprv stačí vedieť počítať, deliť 2, sčítať a odčítať. Po druhé, môžete nájsť oblasť a zložitý tvar bez toho, aby ste trávili veľa času. Po tretie, tento vzorec funguje pre akýkoľvek mnohouholník.

Nevýhodou je, že výberový vzorec je použiteľný len pre tvary, ktoré sú nakreslené na kockovanom papieri a vrcholy ležia v uzloch buniek.

Som si istý, že pri zložení záverečných skúšok problémy s výpočtom plochy čísel nespôsobia ťažkosti. Koniec koncov, už poznám Pickov vzorec.

Bibliografia

Bunimovich E.A., Dorofeev G.V., Suvorova S.B. a iná matematika. Aritmetika. Geometria. 5. stupeň: vzdelávací. pre všeobecné vzdelanie. organizácie s adj. k elektrónu. nosič-3.vyd.-M .: Vzdelávanie, 2014.- 223, s. : chorý. - (Gule).

Bunimovich E.A., Kuznetsova L.V., Minaeva S.S. a iná matematika. Aritmetika. Geometria. 6. stupeň: vzdelávací. pre všeobecné vzdelanie. organizácie-5.vyd.-M .: Vzdelávanie, 2016.-240s. : chorý - (Gule).

Vasiliev N.B. Okolo Pickovho vzorca. // Množstvo - 1974.-№2. -s. 39-43

Rassolov V.V. Úlohy z planimetrie. / 5. vyd., Rev. A pridajte. - M .: 2006.-640. roky.

I.V. Jaščenko, OGE. Matematika: typické možnosti skúšania: O-39 36 možností - M .: Národné osvetové nakladateľstvo, 2017. -240 s. - (OGE. FIPI-škola).

"Vyriešim OGE": matematika. Tréningový systém Dmitrija Gushchina. OGE-2017: úlohy, odpovede, riešenia [Elektronický zdroj]. Režim prístupu: https://oge.sdamgia.ru/test?id=6846966 (dátum ošetrenia 4.2.2017)

Pomocou vzorca Pick môžete nájsť oblasť postavy postavenej na hárku v bunke (trojuholník, štvorec, lichobežník, obdĺžnik, mnohouholník).

V úlohách, ktoré budú na skúške, je celá skupina úloh, v ktorých je daný mnohouholník, postavený na hárku v bunke a otázka je o nájdení oblasti. Mierka bunky je jeden štvorcový centimeter.

Zobraziť obsah prezentácie

Georg Peak

Georg Alexander Peak,

rakúsky matematik

(10.08.1859 - 13.07.1942)

Vzorec bol objavený v roku 1899.

Oblasť požadovaného čísla možno nájsť podľa vzorca:

M je počet uzlov na hranici trojuholníka (na stranách a vrcholoch):
N je počet uzlov vo vnútri trojuholníka;

* Pod "uzlami" rozumieme priesečník čiar.

Nájdite oblasť trojuholníka:

Označme uzly:

1 bunka = 1 cm

M = 15 (označené červenou farbou)
N = 34 (označené modrou farbou)

Nájdite oblasť rovnobežníka:

Označme uzly:

M = 18 (označené červenou farbou)
N = 20 (označené modrou farbou)

Nájdite oblasť lichobežníka:

Označme uzly:

M = 24 (označené červenou farbou)
N = 25 (označené modrou farbou)

Nájdite oblasť polygónu:

Označme uzly:

M = 14 (označené červenou farbou)
N = 43 (označené modrou farbou)

Označme uzly:

M = 11 (označené červenou farbou)
N = 5 (označené modrou farbou)

Rozhodnite sa sami:

1. Nájdite oblasť štvoruholníka znázorneného na kockovanom papieri s veľkosťou bunky 1 cm x 1 cm. Odpoveď uveďte v centimetroch štvorcových.

4. Nájdite plochu štvoruholníka zobrazenú na kockovanom papieri s veľkosťou bunky 1 cm x 1 cm. Odpoveď uveďte v centimetroch štvorcových .

Opíšme obdĺžnik v jeho blízkosti:

Od plochy obdĺžnika (v tomto prípade je to štvorec) odčítame plochy výsledných jednoduchých obrázkov:

odpovede:

№ úlohy

možnosť 1

Možnosť 2

Možnosť 3

Možnosť 4

Vrcholový vzorec

Sazhina Valeria Andreevna, študent 9. ročníka, MAOU "Stredná škola č. 11" Ust-Ilimsk, Irkutská oblasť

vedúci: Gubar Oksana Mikhailovna, učiteľ matematiky najvyššej kvalifikačnej kategórie MAOU "Stredná škola č. 11" Usť-Ilimsk, Irkutská oblasť

rok 2016

Úvod

Pri štúdiu témy geometrie „Plochy mnohouholníkov“ som sa rozhodol zistiť: existuje spôsob, ako nájsť oblasti odlišné od oblastí, ktoré sme študovali v lekciách?

Toto je vzorec Peak. L. V. Gorina v „Materiáloch pre sebavzdelávanie študentov“ opísal tento vzorec takto: „Zoznámenie sa s Pickovým vzorcom je obzvlášť dôležité v predvečer USE a Štátnej skúšobnej agentúry. Pomocou tohto vzorca môžete ľahko vyriešiť veľkú triedu problémov ponúkaných pri skúškach - to sú problémy s nájdením oblasti polygónu znázornenej na kockovanom papieri. Pickov malý vzorec nahradí celý súbor vzorcov potrebných na riešenie takýchto problémov. Pickov vzorec bude fungovať "jeden za všetkých ..."! ".

V materiáloch skúšky som narazil na problémy s praktickým obsahom pri hľadaní výmer pozemkov. Rozhodol som sa skontrolovať, či je tento vzorec použiteľný na nájdenie oblasti školského územia, mestských mikrookresov a regiónu. A tiež je racionálne používať ho na riešenie problémov.

Predmet výskumu: Peakov vzorec.

Predmet výskumu: racionalita aplikácie Pickovho vzorca pri riešení problémov.

Účel práce: zdôvodniť racionálnosť použitia Pickovho vzorca pri riešení problémov s nájdením oblasti obrázkov zobrazených na kockovanom papieri.

Metódy výskumu: modelovanie, porovnávanie, zovšeobecňovanie, analógie, štúdium literárnych a internetových zdrojov, analýza a klasifikácia informácií.

Vyberte potrebnú literatúru, analyzujte a systematizujte prijaté informácie;

Zvážte rôzne metódy a techniky riešenia problémov na kockovanom papieri;

Experimentálne skontrolujte racionálnosť použitia vzorca Pick;

Zvážte použitie tohto vzorca.

Hypotéza: ak použijete vzorec Peak na nájdenie oblastí mnohouholníka, potom môžete nájsť oblasť územia a riešenie problémov na kockovanom papieri bude racionálnejšie.

Hlavná časť

Teoretická časť

Kockovaný papier (presnejšie jeho uzly), na ktorý často najradšej kreslíme a kreslíme, je jedným z najdôležitejších príkladov bodkovanej mriežky na rovine. Už táto jednoduchá mriežka slúžila ako východiskový bod pre K. Gaussa na porovnanie plochy kruhu s počtom bodov s celočíselnými súradnicami umiestnenými v ňom. Skutočnosť, že niektoré jednoduché geometrické tvrdenia o obrazcoch v rovine majú hlboké dôsledky v aritmetických štúdiách, výslovne poznamenal G. Minkowski v roku 1896, keď prvýkrát použil geometrické metódy na zváženie číselných teoretických problémov.

Nakreslíme si mnohouholník na kockovaný papier (Príloha 1, Obrázok 1). Skúsme teraz vypočítať jeho plochu. Ako to spraviť? Asi najjednoduchšie je rozdeliť ho na pravouhlé trojuholníky a lichobežník, ktorých plochy sa už dajú ľahko vypočítať a výsledky sčítať.

Použitá metóda je jednoduchá, ale veľmi ťažkopádna, navyše nie je vhodná pre všetky polygóny. Takže nasledujúci mnohouholník nemôže byť rozdelený na pravouhlé trojuholníky, ako sme to urobili v predchádzajúcom prípade (Príloha 2, Obrázok 2). Môžete ho napríklad skúsiť doplniť na „dobrý“, ktorý potrebujeme, teda na taký, ktorého plochu vieme vypočítať opísaným spôsobom, potom odčítajte plochy pripočítanej diely z výsledného čísla.

Ukazuje sa však, že existuje veľmi jednoduchý vzorec, ktorý vám umožňuje vypočítať plochy takýchto mnohouholníkov s vrcholmi v uzloch štvorcovej siete.

Tento vzorec objavil rakúsky matematik Pik Georg Aleksandrov (1859 - 1943) v roku 1899. Okrem tohto vzorca Georg Pieck objavil vety Pieck, Pieck - Julia, Pieck - Nevalina a dokázal Schwarz - Pieck nerovnosť.

Tento vzorec zostal nejaký čas nepovšimnutý potom, čo ho Peek zverejnil, ale v roku 1949 poľský matematik Hugo Steinhaus zahrnul vetu do svojho slávneho matematického kaleidoskopu. Od tej doby sa Pickova veta stala všeobecne známou. V Nemecku je Pickov vzorec súčasťou školských učebníc.

Je to klasický výsledok kombinatorickej geometrie a geometrie čísel.

Dôkaz Pickovho vzorca

Nech ABCD je obdĺžnik s vrcholmi v uzloch a stranách pozdĺž čiar mriežky (príloha 3, obrázok 3).

Označme В - počet uzlov ležiacich vo vnútri obdĺžnika a Г - počet uzlov na jeho hranici. Posuňte mriežku o polovicu bunky doprava a o polovicu bunky

cesta dole. Potom možno územie obdĺžnika „rozdeliť“ medzi uzly nasledovne: každý z uzlov B „ovláda“ celú bunku posunutej mriežky a každý z uzlov G – 4 hraničné nerohové uzly – polovicu bunky a každý z rohových bodov - štvrtina bunky. Preto sa plocha obdĺžnika S rovná

S = B+ + 4 = B+ - 1 .

Takže pre obdĺžniky s vrcholmi v uzloch a na stranách pozdĺž čiar mriežky nastavíme vzorec S = B + - 1 . Toto je Pickov vzorec.

Ukazuje sa, že tento vzorec platí nielen pre obdĺžniky, ale aj pre ľubovoľné polygóny s vrcholmi v uzloch mriežky.

Praktická časť

Nájdenie oblasti obrázkov pomocou geometrickej metódy a vzorca Pick

Rozhodol som sa uistiť, že Pickov vzorec je správny pre všetky príklady, na ktoré som sa pozrel.

Ukazuje sa, že ak je možné polygón rozrezať na trojuholníky s vrcholmi v uzloch mriežky, platí preň Pickov vzorec.

Skontroloval som niektoré problémy na kockovanom papieri s bunkami s rozmermi 1 cm1 cm a vykonal som porovnávaciu analýzu na riešenie problémov (tabuľka 1).

Tabuľka č. 1 Riešenie problémov rôznymi spôsobmi.

Kreslenie

Podľa geometrického vzorca

Podľa vzorca Peak

Problém číslo 1

S = S NS - (2S 1 + 2S 2 )

S NS =4*5=20 cm 2

S 1 =(2*1)/2=1 cm 2

S 2 =(2*4)/2=4 cm 2

S = 20- (2 * 1 + 2 * 4) = 10 cm 2

Odpoveď :10 cm ².

B = 8, G = 6

S= 8 + 6/2 - 1 = 10 (cm²)

Odpoveď: 10 cm².

Problém číslo 2

a = 2, h = 4

S = a * h = 2 * 4 = 8 cm 2

Odpoveď : 8 cm ².

B = 6, G = 6

S= 6 + 6/2 - 1 = 8 (cm²)

Odpoveď: 8 cm².

Problém číslo 3

S = S sq - (S 1 + 2S 2 )

S sq =4 2 =16 cm 2

S 1 = (3 * 3) / 2 = 4,5 cm2

S 2 = (1 * 4) / 2 = 2 cm2

S= 16- (4,5 + 2 * 2) = 7,5 cm2

B = 6, G = 5

S= 6 + 5/2 - 1 = 7,5 (cm²)

Odpoveď: 7,5 cm².

Problém číslo 4

S = S NS - (S 1 + S 2+ S 3 )

S NS =4 * 3=12 cm 2

S 1 =(3*1)/2=1,5 cm 2

S 2 =(1*2)/2=1 cm 2

S 3 =(1+3)*1/2=2 cm 2

S = 12- (1,5 + 1 + 2) = 7,5 cm 2

B = 5, G = 7

S= 5 + 7/2 - 1 = 7,5 (cm²)

Odpoveď: 7,5 cm².

Problém č. 5.

S = S NS - (S 1 + S 2+ S 3 )

S NS =6 * 5=30 cm 2

S 1 =(2*5)/2=5 cm 2

S 2 =(1*6)/2=3 cm 2

S 3 =(4*4)/2=8 cm 2

S = 30- (5 + 3 + 8) = 14 cm 2

Odpoveď: 14 cm²

H = 12, G = 6

S= 12 + 6/2 - 1 = 14 (cm²)

Odpoveď: 14 cm²

Úloha №6.

S tr = (4 + 9) / 2 * 3 = 19,5 cm2

Odpoveď: 19,5 cm 2

H = 12, G = 17

S= 12 + 17/2 - 1 = 19,5 (cm²)

Odpoveď: 19,5 cm 2

Úloha №7. Nájdite plochu lesa (v m²) zobrazenú na pláne so štvorcovou sieťou 1 × 1 (cm) v mierke 1 cm - 200 m

S = S 1 + S 2+ S 3

S 1 =(800*200)/2=80000 m 2

S 2 =(200*600)/2=60000 m 2

S 3 =(800+600)/2*400=

280000 m 2

S = 80000+60000+240000=

420 000 m2

Odpoveď: 420 000 m²

B = 8, G = 7. S= 8 + 7/2 - 1 = 10,5 (cm²)

1 cm² - 200² m²; S= 40 000 10,5 = 420 000 (m2)

Odpoveď: 420 000 m²

Problém číslo 8 ... Nájdite plochu poľa (v m²) znázornenú na pláne so štvorcovou sieťou 1 × 1 (cm) v mierke

1 cm - 200 m.

S= Sštvorcových -2 ( S tr + S rebrík)

Sštvorcový = 800 * 800 = 640 000 m2

S tr = (200 * 600) / 2 = 60 000 m2

S rebrík = (200 + 800) / 2 * 200 =

100 000 m2

S=640000-2(60000+10000)=

320 000 m 2

Odpoveď: 320 000 m²

Riešenie. Nájsť Splocha štvoruholníka zobrazená na kockovanom papieri podľa Pickovho vzorca:S= B + - 1

B = 7, G = 4. S= 7 + 4/2 - 1 = 8 (cm²)

1 cm² - 200² m²; S= 40 000 8 = 320 000 (m2)

Odpoveď: 320 000 m²

Problém číslo 9 ... Nájdite oblasťS sektory, berúc do úvahy strany štvorcových buniek rovné 1. Vo svojej odpovedi uveďte .

Sektor je jedna štvrtina kruhu, a preto sa jeho plocha rovná jednej štvrtine plochy kruhu. Plocha kruhu je πR 2 , kde R Je polomer kruhu. V našom prípadeR =√5 a teda oblasťS sektor je 5π / 4. KdeS/ π = 1,25.

Odpoveď. 1.25.

G = 5, B = 2, S= B + G / 2 - 1 = 2 + 5/2 - 1 = 3,5, ≈ 1,11

Odpoveď. 1.11.

Problém číslo 10. Nájdite oblasť S krúžky, počítajúc strany štvorcových buniek rovné 1. Vo svojej odpovedi uveďte .

Plocha prstenca sa rovná rozdielu medzi plochami vonkajšieho a vnútorného kruhu. PolomerR vonkajší kruh je

2, polomer r vnútorný kruh je 2. Preto je plocha prsteňa 4a preto... odpoveď: 4.

G = 8, B = 8, S= B + G / 2 - 1 = 8 + 8/2 - 1 = 11, ≈ 3,5

Odpoveď: 3.5

Záver: Uvažované úlohy sú podobné úlohe z možností na kontrolné a meracie materiály skúšky z matematiky (úlohy č. 5, 6).

Z uvažovaných riešení úloh som videl, že niektoré z nich, napríklad úlohy č. 2.6, je jednoduchšie riešiť pomocou geometrických vzorcov, keďže výšku a základňu je možné určiť z obrázku. Vo väčšine úloh je však potrebné figúrku rozdeliť na jednoduchšie (úloha č. 7) alebo zostaviť do tvaru obdĺžnika (úlohy č. 1,4,5), štvorca (úlohy č. 3,8).

Pri riešení úloh # 9 a # 10 som videl, že aplikovanie Pickovho vzorca na tvary, ktoré nie sú polygóny, dáva približný výsledok.

Aby som skontroloval racionalitu vzorca Peak, vykonal som štúdiu na tému stráveného času (príloha 4, tabuľka č. 2).

Záver: z tabuľky a diagramu (príloha 4, diagram 1) je vidieť, že pri riešení úloh pomocou vzorca Peak sa strávi oveľa menej času.

Nájdenie povrchovej plochy priestorových tvarov

Overme si použiteľnosť tohto vzorca na priestorové formy (príloha 5, obrázok 4).

Nájdite celkovú plochu obdĺžnikového rovnobežnostena za predpokladu, že strany štvorcových buniek sú 1.

Toto je chyba vo vzorci.

Aplikácia vzorca Peak na nájdenie oblasti územia

Pri riešení problémov s praktickým obsahom (úlohy č. 7,8; tabuľka č. 1) som sa rozhodol použiť túto metódu na nájdenie oblasti územia našej školy, mikrookresov mesta Ust-Ilimsk, Irkutsk regiónu.

Po preštudovaní „Projektu hraníc pozemku MAUSOSH č. 11 v Usť-Ilimsku“ (Príloha 6) som našiel výmeru územia našej školy a porovnal som ju s výmerou podľa návrhu hraníc hl. pozemok (príloha 9, tabuľka 3).

Po preskúmaní mapy pravobrežnej časti Usť-Ilimska (príloha 7) som vypočítal oblasti mikrookresov a porovnal som ich s údajmi z „Generálneho plánu Usť-Ilimska, oblasť Irkutsk“. Výsledky sú uvedené v tabuľke (príloha 9, tabuľka 4).

Po preskúmaní mapy regiónu Irkutsk (príloha 7) som našiel oblasť územia a porovnal som ju s údajmi z Wikipédie. Výsledky sú uvedené v tabuľke (príloha 9, tabuľka 5).

Po analýze výsledkov som dospel k záveru: pomocou vzorca Peak sa tieto oblasti dajú nájsť oveľa jednoduchšie, ale výsledky sú približné.

Z uskutočneného výskumu som získal najpresnejšiu hodnotu pri zistení plochy školského územia (Príloha 10, diagram 2). Väčší nesúlad vo výsledkoch bol získaný pri hľadaní oblasti Irkutskej oblasti (príloha 10, diagram 3). Je to spôsobené skutočnosťou. Že nie všetky hranice oblasti sú polygónové strany a vrcholy nie sú kotviace body.

Záver

Výsledkom mojej práce bolo rozšírenie vedomostí o riešení úloh na kockovanom papieri, ktoré si určilo klasifikáciu skúmaných problémov.

Pri vykonávaní práce sa riešili problémy nájsť oblasť polygónov zobrazených na kockovanom papieri dvoma spôsobmi: geometrickým a pomocou Pickovho vzorca.

Analýza riešení a experiment na určenie stráveného času ukázali, že aplikácia vzorca umožňuje racionálnejším spôsobom riešiť problémy na nájdenie oblasti polygónu. To šetrí čas na skúške z matematiky.

Nájdenie oblasti rôznych obrázkov zobrazených na kockovanom papieri umožnilo dospieť k záveru, že použitie Pickovho vzorca na výpočet plochy kruhového sektora a prstenca je nepraktické, pretože poskytuje približný výsledok, a že Pickov vzorec sa nepoužíva na riešenie problémov vo vesmíre.

V práci boli tiež nájdené oblasti rôznych území pomocou vzorca Peak. Môžeme dospieť k záveru, že použitie vzorca na nájdenie oblasti rôznych území je možné, ale výsledky sú približné.

Mnou predložená hypotéza sa potvrdila.

Prišiel som na to, že téma, ktorá ma zaujala, je dosť mnohostranná, úlohy na kockovanom papieri sú rôznorodé, rôznorodé sú aj metódy a techniky ich riešenia. Preto som sa rozhodol pokračovať v práci týmto smerom.

Literatúra

Volkov SD .. Návrh hranice pozemku, 2008, s. 16.

Gorina L.V., Matematika. Všetko pre učiteľa, M: Nauka, 2013, č. 3, s. 28.

Prokopyeva V.P., Petrov A.G., Celkový plán mesta Ust-Ilimsk, región Irkutsk, Gosstroy Ruska, 2004 s. 65.

Riss E.A., Zharkovskaya N.M., Geometria kockovaného papiera. Pickov vzorec. - Moskva, 2009, č. 17, s. 24-25.

Smirnová I. M.,. Smirnov V. A, Geometria na kockovanom papieri. - Moskva, Chistye Prudy, 2009, s. 120.

Smirnova I.M., Smirnov V.A., Geometrické problémy s praktickým obsahom. - Moskva, Chistye Prudy, 2010, s. 150

Problémy otvorenej banky úloh z matematiky FIPI, 2015.

Mapa mesta Ust-Ilimsk.

Mapa oblasti Irkutsk.

Wikipedia.

Vrcholový vzorec

1. Úvod

2. Pickov vzorec. Dôkaz o I.

Dôkaz II.

Dôkaz Sh.

3. Úlohy.

4. Vzorec pre oblasť mnohouholníka cez súradnice vrcholov.

5. Úlohy.

6. Literatúra

Pickov vzorec.

1. Úvod.

Múdrosť čerpáme z histórie,

v poézii - vtip,

v matematike, rozlišovanie.

F. Bacon

Dej sa bude odvíjať na bežnom károvanom papieri.

Čiary prebiehajúce po stranách buniek tvoria mriežku a vrcholy buniek tvoria uzly tejto mriežky. Nakreslíme na list mnohouholník s vrcholmi v uzloch a nájdeme jeho plochu.

Môžete ho hľadať rôznymi spôsobmi. Môžete napríklad rozrezať mnohouholník na pomerne jednoduché tvary, nájsť ich oblasti a zložiť ich.

Ale tu nás čaká veľa problémov. Postavu možno ľahko rozložiť na obdĺžniky, lichobežníky a trojuholníky a bez námahy vypočítate jej plochu.

Hoci polygón vyzerá dostatočne jednoducho, výpočet jeho plochy dá veľa práce. Čo keby ten polygón vyzeral bizarnejšie? Ukazuje sa, že oblasti polygónov, ktorých vrcholy sa nachádzajú v uzloch mriežky, sa dajú vypočítať oveľa jednoduchšie: existuje vzorec, ktorý spája ich plochu s počtom uzlov ležiacich vo vnútri a na hranici mnohouholníka. Tento úžasný a jednoduchý vzorec sa nazýva Pickov vzorec.

2. Pickov vzorec.

Vrcholy mnohouholníka (nie nevyhnutne konvexné) sa nachádzajú v uzloch celočíselnej mriežky. Vo vnútri leží B uzly mriežky a na hranici Γ uzlov. Dokážme, že jeho plocha sa rovná B + - 1 (Pickov vzorec).

Dôkaz o I.

Uvažujme mnohouholník, ktorého vrcholy sú v uzloch celočíselnej mriežky, to znamená, že majú celočíselné súradnice.

Rozdeľte mnohouholník na trojuholníky s vrcholmi v uzloch mriežky, ktoré neobsahujú uzly ani vo vnútri, ani po stranách.

Označme:

n- počet strán mnohouholníka,

m- počet trojuholníkov s vrcholmi v uzloch mriežky, ktoré neobsahujú uzly ani vo vnútri, ani na stranách,

B - počet uzlov vo vnútri polygónu,

Г je počet uzlov na stranách vrátane vrcholov.

Plochy všetkých týchto trojuholníkov sú rovnaké a rovnaké.

Preto je plocha polygónu
.

180 0 m .

Teraz zistime túto sumu iným spôsobom.

Súčet uhlov s vrcholom v akomkoľvek vnútornom uzle je 360 0.

Potom súčet uhlov s vrcholmi vo všetkých vnútorných uzloch je 360 0 V.

Celkový súčet uhlov v uzloch na stranách, ale nie vo vrcholoch, sa rovná 180 0 (Г - n).

Súčet uhlov vo vrcholoch mnohouholníka je 180 0 ( n – 2) .

Celkový súčet uhlov všetkých trojuholníkov je 360 0 V + 180 0 (G - n) + 180 0 (n – 2).

Teda 1800 m= 360 0 V + 180 0 (G - n) + 180 0 (n – 2),

180 0 m= 360 0 V + 180 0 G - 180 0 n + 180 0 n- 180 0 2,

180 0 m= 360 0 V + 180 0 G - 360 0,

= B+ – 1 ,

odkiaľ dostaneme výraz pre oblasť S mnohouholníka:

S= B+ – 1 ,

známy ako Pickov vzorec.

Na obrázku: B = 24, G = 9, tedaS = 24 + – 1 = 27,5.

Nájdite oblasť prvého mnohouholníka pomocou vzorca Pick:

B = 28 (zelené bodky);

G = 20 (modré bodky).

Dostávame, S =
= 37 štvorcových jednotiek

Dôkaz II.

Každému polygónu M s vrcholmi v uzloch celočíselnej mriežky priradíme číslo f (M) =
, kde sa sčítanie vykonáva cez všetky uzly mriežky patriace do M a uhol je definovaný nasledovne: =
pre vnútorný bod mnohouholníka, =
pre hraničný bod iný ako vrchol a - uhol vo vrchole, ak je daný uzol vrcholom. Je ľahké vidieť, že f (M) =
+
= B+ - 1. Zostáva skontrolovať, či sa číslo f (M) rovná ploche mnohouholníka M.

Nech je mnohouholník M rozrezaný na mnohouholníky M 1 a M 2 s vrcholmi v uzloch mriežky. Potom f (M) = f (M 1) + f (M 2), pretože uhly sa pre každý uzol sčítavajú. Ak teda Pickov vzorec platí pre dva z polygónov M, M 1 a M 2, platí to aj pre tretí.

Ak M je obdĺžnik so stranami p a q smerované pozdĺž mriežkových línií, potom

f (M) = (p - 1) (q - 1) +
= pq.

V tomto prípade platí Pickov vzorec. Rozrezanie obdĺžnika M s uhlopriečkou na trojuholníky M 1 a M 2 a s využitím faktu, že f (M) = f (M 1) + f (M 2) a f (M 1) = f (M 2), je jednoduché. dokázať Pickov vzorec pre akýkoľvek pravouhlý trojuholník s nohami nasmerovanými pozdĺž čiar mriežky. Odrezaním niekoľkých z týchto trojuholníkov z obdĺžnika môžete získať akýkoľvek trojuholník.

Na dokončenie dôkazu Pickovho vzorca zostáva poznamenať, že ľubovoľný mnohouholník môže byť rozdelený na trojuholníky pomocou nesúvislých uhlopriečok.

Dôkaz Sh.

Vzťah medzi plochou tvaru a počtom uzlov, ktoré spadajú do tohto tvaru, je obzvlášť jasný v prípade obdĺžnika.

Nechať byť A B C D- obdĺžnik s vrcholmi na uzloch a stranách pozdĺž čiar mriežky.

Označme podľa V počet uzlov ležiacich vo vnútri obdĺžnika a po ňom G- počet uzlov na jeho hranici. Posuňte mriežku o polovicu bunky doprava a o polovicu nadol.

Potom môže byť územie obdĺžnika "rozložené" medzi uzlami takto: každý z V uzly "riadia" celú bunku posunutej mriežky, každý z G- 4 hraničné nerohové uzly - polovica bunky a každý z rohových bodov - štvrtina bunky. Preto sa plocha obdĺžnika S rovná

Takže pre obdĺžniky s vrcholmi v uzloch a na stranách pozdĺž čiar mriežky nastavíme vzorec

Dokážme, že tento vzorec platí nielen pre obdĺžniky, ale aj pre ľubovoľné polygóny s vrcholmi v uzloch mriežky.

Označme podľa S m oblasť polygónuM s vrcholmi v uzloch a cezNS m - hodnota
, kdeV m - počet uzlov vo vnútriM, a G m - počet uzlov na hranici. Potom môže byť Pickov vzorec napísaný ako
.

Dôkaz vzorca sme rozdelili do niekoľkých krokov.

Krok 1.

Ak polygónM s vrcholmi v uzloch mriežky je rozrezaný na 2 polygónyM 1 a M 2 , majú tiež vrcholy iba v uzloch mriežky
... Nechajte polygónM rozrezané na mnohouholníkyM 1 a M 2 s vrcholmi v uzloch podľa segmentov AB. Všetky uzly, okrem tých, ktoré spadajú do segmentuAB, dajte rovnaký príspevok na ľavú a pravú stranu vzorca. Zvážte uzly ležiace na segmente AB.

Ak takýto uzol leží medzi A a B (napríklad C), potom pre mnohouholníkM je vnútorný, ale pre polygónyM 1 a M 2 - hranica. Preto jeho príspevok kNS m sa rovná 1 a v každom z výrazov
a
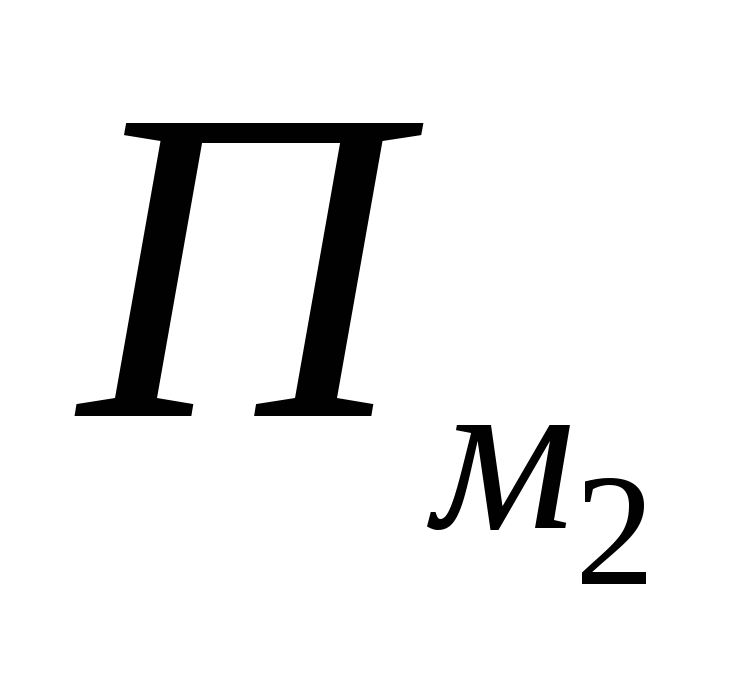- 0,5 každý, to znamená príspevky takéhoto uzla doNS m a
sú si rovní.

Uvažujme uzly A a B. Sú hraničné ako pre M a pre M 1 , M 2 .

Preto príspevok každého z týchto uzlov kNS m sa rovná 0,5 palca
- jednotka. Preto celkový príspevok uzlov A a B kNS m sa rovná 1, čo je o 1 menej ako ich príspevok k
. ale
, a.

Z celkového „príspevku“ všetkých uzlov NS m odčíta 1 a od
odpočítajte 2 a to kompenzuje rozdiel v príspevkoch uzlov A a B.

takze
.

Krok 2.

Ak polygón M s vrcholmi v bodoch siete je rozrezaný na dva polygóny M 1 a M 2 (aj s vrcholmi v uzloch) a vzorec je správny pre niektoré dva z polygónov MM 1 , M 2 , potom to platí aj pre tretí polygón.

Napríklad nech platí preM 1 a M 2 , to jest
... Potom (podľa prvého kroku), ale na prvý krok) posledný výraz jeNS m , a rovnosť
a existuje Peakov vzorec.

Krok 3

Dokážme Pickov vzorec pre pravouhlý trojuholník s vrcholmi v uzloch mriežky a nohami ležiacimi na čiarach mriežky.

Trojuholník ABC postaviť do obdĺžnika A B C D .

Pre obdĺžniky je Pickov vzorec správny: S A B C D = P A B C D . Podľa prvého kroku NS A B C D = P ABC + P ACD , NS ABC = P ACD , tak NS A B C D = 2P ABC . ale S A B C D = 2 S ABC ... Preto S ABC = P ABC .

Krok 4

Pickov vzorec platí pre ľubovoľný trojuholník s vrcholmi v bodoch mriežky.

Pri pohľade na obrázok je ľahké pochopiť: každý takýto trojuholník možno získať „odrezaním“ z nejakého obdĺžnika so stranami pozdĺž čiar mriežky niekoľkých obdĺžnikov a pravouhlých trojuholníkov s nohami na čiarach mriežky. A keďže Pickov vzorec platí pre obdĺžniky a pravouhlé trojuholníky, potom (pripomeňte si krok 2) platí aj pre pôvodný trojuholník.

Dokázali sme, že ak je možné polygón rozrezať na trojuholníky s vrcholmi v uzloch mriežky, potom platí Pickov vzorec.

3. Úlohy.

Nájdite oblasti tvarov:

1
.