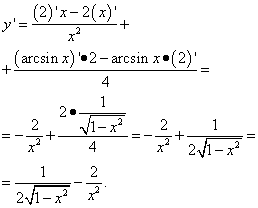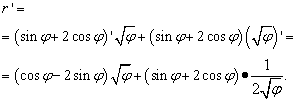Odvod kosinusa: (cos x)′. Odvodi trigonometričnih funkcij: tangens, sinus, kosinus in drugi

Poiščite izpeljanko.

Možnost 1.

Možnost 2.

pri = 2X + 5.

pri = 2X – 5.

pri= 4cos X.

pri= 3 sin X.

pri= tg X+ctg X.

pri= tg X-ctg X.

pri= greh 3 X.

pri= cos 4 X.

Možnosti odgovora.

– 4sin X

– 3 cos X

1/cos 2 X+ 1/greh 2 X

1/cos 2 X–1/greh 2 X

1/greh 2 X–1/cos 2 X

– 4sin4 X

– 3cos3 X

f(x) = greh x+cos x

f(x) = greh 2 x – x

f(x) = 2x+cos(4 x – )

Možnost 1

Možnost 2

l = 2X 3

l = 3X 2

l = 1/4 X 4 + 2X 2 – 7

l = 1/2 X 4 + 4X + 5

l = X 3 + 4X 2 – 3X.
Reši enačbo l " = 0

l = 2X 3 – 9X 2 + 12X + 7.
Reši enačbo l " = 0.

l= greh 2 X– ker 3 X.

l= cos 2 X– greh 3 X.

l= tg X–ctg( X + /4).

l=ctg X+ tg( X – /4).

l= greh 2 X.

l= cos 2 X.

Možnosti odgovora.

Pri izpeljavi prve formule tabele bomo izhajali iz definicije odvodne funkcije v točki. Vzemimo kam x- kaj realno število, to je x– poljubno število iz domene definicije funkcije. Zapišimo mejo razmerja prirastka funkcije in prirastka argumenta pri :

Opozoriti je treba, da pod mejnim znakom dobimo izraz, ki ni negotovost ničle, deljene z ničlo, saj števec ne vsebuje neskončno majhne vrednosti, ampak natančno nič. Z drugimi besedami, prirastek konstantne funkcije je vedno enak nič.

torej odvod konstantne funkcijeje enak nič v celotnem področju definicije.

Odvod potenčne funkcije.

Formula za odvod potenčne funkcije ima obliko , kjer je eksponent str– poljubno realno število.

Najprej dokažimo formulo za naravni eksponent, to je za p = 1, 2, 3, …

Uporabili bomo definicijo derivata. Zapišimo mejo razmerja med prirastkom potenčne funkcije in prirastkom argumenta:

Za poenostavitev izraza v števcu se obrnemo na Newtonovo binomsko formulo:

torej

To dokazuje formulo za odvod potenčne funkcije za naravni eksponent.

Odvod eksponentne funkcije.

Predstavljamo izpeljavo formule za izpeljavo na podlagi definicije:

Prišli smo do negotovosti. Da ga razširimo, uvedemo novo spremenljivko in pri . Potem. Pri zadnjem prehodu smo uporabili formulo za prehod na novo logaritemsko osnovo.

Nadomestimo v prvotno mejo:

Če se spomnimo druge izjemne meje, pridemo do formule za odvod eksponentne funkcije:

Odvod logaritemske funkcije.

Dokažimo formulo za odvod logaritemske funkcije za vse x iz domene definicije in vse veljavne vrednosti baze a logaritem Po definiciji derivata imamo:

Kot ste opazili, so bile med dokazom transformacije izvedene z uporabo lastnosti logaritma. Enakopravnost je res zaradi druge izjemne meje.

Odvodi trigonometričnih funkcij.

Za izpeljavo formul za odvode trigonometričnih funkcij se bomo morali spomniti nekaterih trigonometričnih formul, pa tudi prve izjemne limite.

Po definiciji odvoda za sinusno funkcijo imamo .

Uporabimo formulo razlike sinusov:

Obrnemo se še na prvo izjemno mejo:

Torej odvod funkcije greh x Tukaj je cos x.

Formula za odvod kosinusa se dokaže na povsem enak način.

Zato je odvod funkcije cos x Tukaj je – greh x.

Izpeljali bomo formule za tabelo odvodov za tangens in kotangens z uporabo preverjenih pravil diferenciacije (odvod ulomka).

Odvodi hiperboličnih funkcij.

Pravila diferenciacije in formula za odvod eksponentne funkcije iz tabele odvodov nam omogočajo izpeljavo formul za odvode hiperboličnega sinusa, kosinusa, tangensa in kotangensa.

Odvod inverzne funkcije.

Da ne bi prišlo do zmede med predstavitvijo, označimo v indeksu argument funkcije, s katero se izvaja diferenciacija, to je odvod funkcije f(x) Avtor: x.

Zdaj pa oblikujmo pravilo za iskanje odvoda inverzne funkcije.

Naj funkcije y = f(x) in x = g(y) medsebojno inverzni, definirani na intervalih oz. Če v neki točki obstaja končna ničelna odvodnja funkcije f(x), potem je v točki končni odvod inverzne funkcije g(y), in . V drugi objavi .

To pravilo je mogoče preoblikovati za katero koli x iz intervala , potem dobimo .

Preverimo veljavnost teh formul.

Poiščimo inverzno funkcijo za naravni logaritem (Tukaj l je funkcija in x- prepir). Po rešitvi te enačbe za x, dobimo (tukaj x je funkcija in l– njen argument). to je in medsebojno inverzne funkcije.

Iz tabele izpeljank vidimo, da in .

Prepričajmo se, da nas formule za iskanje odvodov inverzne funkcije vodijo do enakih rezultatov:

Predstavljen je dokaz in izpeljava formule za odvod kosinusa - cos(x). Primeri izračuna odvodov cos 2x, cos 3x, cos nx, kosinusa na kvadrat, kuba in na potenco n. Formula za odvod kosinusa n-tega reda.

Odvod spremenljivke x iz kosinusa x je enak minus sinusa x:
(cos x)′ = - sin x.

Dokaz

Za izpeljavo formule za odvod kosinusa uporabimo definicijo odvoda:
.

Transformirajmo ta izraz, da ga zmanjšamo na znane matematične zakone in pravila. Za to moramo poznati štiri lastnosti.
1) Trigonometrične formule. Potrebovali bomo naslednjo formulo:
(1) ;
2) Lastnost kontinuitete sinusne funkcije:
(2) ;
3) Pomen prve izjemne meje:
(3) ;
4) Lastnost limite produkta dveh funkcij:
Če in , potem
(4) .

Uporabimo te zakone do svojih meja. Najprej transformiramo algebraični izraz
.
Za to uporabimo formulo
(1) ;
V našem primeru
; . Potem
;
;
;
.

Naredimo zamenjavo. Ob , . Uporabimo lastnost kontinuitete (2):
.

Naredimo isto zamenjavo in uporabimo prvo izjemno omejitev (3):
.

Ker zgoraj izračunane omejitve obstajajo, uporabimo lastnost (4):

.

Tako smo dobili formulo za odvod kosinusa.

Primeri

Razmislimo preprosti primeri iskanje odvodov funkcij, ki vsebujejo kosinus. Poiščimo izpeljanke naslednje funkcije:
y = cos 2x; y = cos 3x; y = cos nx; y = cos 2 x; y = ker 3 x in y = cos n x.

Primer 1

Poiščite izpeljanke cos 2x, ker 3x in cosnx.

rešitev

Izvirne funkcije imajo podobno obliko. Zato bomo našli odvod funkcije y = cosnx. Potem, kot izpeljanka iz cosnx, nadomestite n = 2 in n = 3 . In tako dobimo formule za derivate ker 2x in ker 3x .

Torej, najdemo odvod funkcije
y = cosnx .
Predstavljajmo si to funkcijo spremenljivke x kot kompleksno funkcijo, sestavljeno iz dveh funkcij:
1)
2)
Potem je izvirna funkcija kompleksna (sestavljena) funkcija, sestavljena iz funkcij in:
.

Poiščimo odvod funkcije glede na spremenljivko x:
.
Poiščimo odvod funkcije glede na spremenljivko:
.
Prijavljamo se.
.
Zamenjajmo:
(P1) .

Zdaj v formuli (A1) nadomestimo in:
;
.

Odgovori

;
;
.

Primer 2

Poiščite odvode kosinusa na kvadrat, kosinusa na kub in kosinusa na potenco n:
y = cos 2 x; y = ker 3 x; y = cos n x.

rešitev

V tem primeru imata tudi funkciji podoben videz. Zato bomo našli izpeljanko največ splošna funkcija- kosinus na potenco n:
y = cos n x.
Nato nadomestimo n = 2 in n = 3. In tako dobimo formule za odvode kosinusa na kvadrat in kosinusa na kub.

Najti moramo torej odvod funkcije
.
Prepišimo ga v bolj razumljivi obliki:
.
Predstavljajmo si to funkcijo kot kompleksno funkcijo, sestavljeno iz dveh funkcij:
1) Funkcije, odvisne od spremenljivke: ;
2) Funkcije, odvisne od spremenljivke: .
Potem je izvirna funkcija kompleksna funkcija, sestavljena iz dveh funkcij in:
.

Poiščite odvod funkcije glede na spremenljivko x:
.
Poiščite odvod funkcije glede na spremenljivko:
.
Uporabimo pravilo diferenciacije kompleksnih funkcij.
.
Zamenjajmo:
(P2) .

Zdaj pa zamenjajmo in:
;
.

Odgovori

;
;
.

Izpeljanke višjega reda

Upoštevajte, da izpeljanka iz cos x prvi vrstni red lahko izrazimo s kosinusom na naslednji način:
.

Poiščimo odvod drugega reda s pomočjo formule za odvod kompleksne funkcije:

.
Tukaj.

Upoštevajte to diferenciacijo cos x povzroči, da se njegov argument poveča za . Potem ima odvod n-tega reda obliko:
(5) .

To formulo je mogoče strožje dokazati z uporabo metode matematične indukcije. Dokaz za n-ti odvod sinusa je predstavljen na strani “Odvod sinusa”. Za n-ti odvod kosinusa je dokaz popolnoma enak. Samo zamenjati morate sin s cos v vseh formulah.

Predstavljeni so odvodi inverznih trigonometričnih funkcij in izpeljava njihovih formul. Podani so tudi izrazi za odvode višjega reda. Povezave do strani s podrobnejšim opisom izpeljave formul.

Najprej izpeljemo formulo za odvod arkusina. Pustiti
y = arcsin x.
Ker je arkus sinus inverzna funkcija sinusa, potem
.
Tukaj je y funkcija x. Diferenciraj glede na spremenljivko x:
.
Prijamo:
.
Tako smo ugotovili:
.

Ker torej. Potem
.
In prejšnja formula ima obliko:
. Od tod
.

Natanko na ta način lahko dobite formulo za odvod ark kosinusa. Vendar pa je lažje uporabiti formulo, ki povezuje inverzne trigonometrične funkcije:
.
Potem
.

Podrobnejši opis je predstavljen na strani “Izpeljava odvodov arksinusa in arkkosinusa”. Tam je dano izpeljava izpeljank na dva načina- obravnavano zgoraj in v skladu s formulo za odvod inverzne funkcije.

Izpeljava odvodov arktangensa in arkotangensa

Na enak način bomo našli izpeljanke arktangensa in arkotangensa.

Pustiti
y = arctan x.
Arktangens je inverzna funkcija tangensa:
.
Diferenciraj glede na spremenljivko x:
.
Uporabimo formulo za odvod kompleksne funkcije:
.
Tako smo ugotovili:
.

Odvod ark kotangensa:
.

Arkusin derivati

Pustiti
.
Odvod arkusina prvega reda smo že našli:
.
Z diferenciacijo najdemo odvod drugega reda:
;
.
Lahko se zapiše tudi v naslednji obliki:
.
Od tu dobimo diferencialno enačbo, ki ji zadostujeta arksinusni odvod prvega in drugega reda:
.

Z razlikovanjem te enačbe lahko najdemo odvode višjega reda.

Odvod arkusina n-te stopnje

Odvod arksinusa reda n ima naslednji pogled:
,
kjer je polinom stopnje . Določeno je s formulami:
;
.
Tukaj.

Polinom zadošča diferencialni enačbi:
.

Odvod arkosinusa n-tega reda

Odvode za ark kosinus dobimo iz odvodov za ark sinus z uporabo trigonometrične formule:
.
Zato se izpeljanke teh funkcij razlikujejo samo po predznaku:
.

Izpeljanke arktangensa

Pustiti . Našli smo odvod ark kotangensa prvega reda:
.

Razčlenimo ulomek na najpreprostejšo obliko:

.
Tukaj je namišljena enota, .

Enkrat diferenciramo in ulomek spravimo na skupni imenovalec:

.

Z zamenjavo dobimo:
.

Odvod arktangensa n-tega reda

Tako je lahko derivat arktangensa n-tega reda predstavljen na več načinov:
;
.

Odvodi ark kotangensa

Naj bo zdaj. Uporabimo formulo, ki povezuje inverzne trigonometrične funkcije:
.
Potem se odvod arktangensa n-tega reda razlikuje le po predznaku od odvoda arktangensa:
.

Z zamenjavo ugotovimo:
.

Reference:
N.M. Gunther, R.O. Kuzmin, Zbirka nalog iz višje matematike, "Lan", 2003.

Najti odvod trigonometrične funkcije potrebo po uporabi tabela izpeljank, in sicer izpeljanke 6-13.

Ko najdete odvodi preprostih trigonometričnih funkcij Da bi se izognili pogostim napakam, bodite pozorni na naslednje točke:

• v funkcijskem izrazu je eden od izrazov pogosto sinus, kosinus ali druga trigonometrična funkcija ne iz argumenta funkcije, temveč iz števila (konstante), zato je izpeljanka tega člena enaka nič;
• skoraj vedno morate poenostaviti izraz, dobljen kot rezultat diferenciacije, in za to morate samozavestno uporabiti znanje o operacijah z ulomki;
• za poenostavitev izraza, ki ga morate skoraj vedno poznati trigonometrične identitete, na primer formula dvojnega kota in formula enote kot vsota kvadratov sinusa in kosinusa.

Primer 1. Poiščite odvod funkcije

rešitev. Recimo z odvod kosinusa vse je jasno, bodo rekli mnogi, ki začnejo preučevati derivate. Kaj pa o derivat sinusa dvanajst deljeno s pi? Odgovor: upoštevajte ga kot nič! Tu je sinus (navsezadnje funkcija!) past, ker argument ni spremenljivka X ali katera koli druga spremenljivka, ampak samo število. To pomeni, da je sinus tega števila tudi število. In odvod števila (konstanta), kot vemo iz tabele odvodov, je enak nič. Torej pustimo samo minus sinus X in poiščemo njegov derivat, ne da bi pozabili na znak:

.

Primer 2. Poiščite odvod funkcije

.

rešitev. Drugi člen je enak kot prvi člen v prejšnjem primeru. To pomeni, da je številka in izpeljanka števila je nič. Odvod drugega člena najdemo kot odvod količnika:

Primer 3. Poiščite odvod funkcije

rešitev. To je še ena težava: tukaj v prvem členu ni arkusina ali druge trigonometske funkcije, obstaja pa x, kar pomeni, da je funkcija x. Zato ga ločimo kot izraz v vsoti funkcij:

Tu so bile potrebne veščine pri operacijah z ulomki, in sicer pri odpravljanju trinadstropne strukture ulomka.

Primer 4. Poiščite odvod funkcije

.

rešitev. Tukaj črka "phi" igra isto vlogo kot "x" v prejšnjih primerih (in v večini drugih, vendar ne v vseh) - neodvisna spremenljivka. Zato, ko iščemo odvod produkta funkcij, ne bomo hiteli, da bi razglasili odvod korena "phi" enak nič. Torej:

Toda rešitev se tu ne konča. Ker so podobni izrazi zbrani v dveh oklepajih, moramo še vedno transformirati (poenostaviti) izraz. Zato pomnožimo oklepaje s faktorji za njimi, nato pa izraze spravimo na skupni imenovalec in izvedemo druge osnovne transformacije:

Primer 5. Poiščite odvod funkcije

rešitev. V tem primeru bomo morali poznati dejstvo, da obstaja takšna trigonometrična funkcija - sekans - in njene formule skozi kosinus. Razlikujmo:

Primer 6. Poiščite odvod funkcije

.

rešitev. V tem primeru se bomo morali spomniti formule dvojnega kota iz šole. Toda najprej ločimo:

,

(to je formula dvojnega kota)