Formule za iskanje enačbe nagnjene tangente. Spletni kalkulator. Enačba premice tangente na graf funkcije v dani točki

Članek vsebuje podrobno razlago definicij, geometrijski pomen izpeljanke z grafični simboli. Na primerih bomo obravnavali enačbo tangente, našli bomo enačbe tangente na krivulje 2. reda.

Yandex.RTB R-A-339285-1 Definicija 1

Naklonski kot premice y = k x + b imenujemo kot α, ki se meri od pozitivne smeri osi x do premice y = k x + b v pozitivni smeri.

Na sliki je smer x označena z zeleno puščico in zelenim lokom, naklonski kot pa z rdečim lokom. Modra črta se nanaša na ravno črto.

Definicija 2

Naklon premice y = k x + b imenujemo numerični koeficient k.

Kotni koeficient je enak tangensu premice, z drugimi besedami k = t g α.

• Nagibni kot premice je enak 0 le, če je vzporedna z x in je naklon enak nič, ker je tangens nič enak 0. To pomeni, da bo oblika enačbe y = b.
• Če je naklonski kot premice y = k x + b oster, potem so izpolnjeni pogoji 0< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0 in na grafu je opaziti povečanje.
• Če je α = π 2, je lokacija premice pravokotna na x. Enakost je podana z x = c, pri čemer je vrednost c realno število.
• Če je kot naklona ravne črte y = k x + b tup, potem ustreza pogojem π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

Definicija 3

Sekanta je premica, ki poteka skozi 2 točki funkcije f (x). Z drugimi besedami, sekans je ravna črta, ki je narisana skozi kateri koli dve točki na grafu dano funkcijo.

Na sliki je razvidno, da je A B sekanta, f (x) pa črna krivulja, α je rdeč lok, ki označuje naklonski kot sekante.

Kdaj naklon premica enaka tangensu naklonskega kota, je jasno, da lahko tangento iz pravokotnega trikotnika A B C najdemo z razmerjem nasprotne strani do sosednje.

Definicija 4

Dobimo formulo za iskanje sekansa oblike:

k = t g α = B C A C = f (x B) - f x A x B - x A, kjer sta abscisi točk A in B vrednosti x A, x B in f (x A), f (x B) so funkcije vrednosti v teh točkah.

Očitno je kotni koeficient sekante določen z enakostjo k = f (x B) - f (x A) x B - x A ali k = f (x A) - f (x B) x A - x B , enačbo pa je treba zapisati kot y = f (x B) - f (x A) x B - x A x - x A + f (x A) ali
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .

Sekans vizualno razdeli graf na 3 dele: levo od točke A, od A do B, desno od B. Spodnja slika prikazuje, da obstajajo tri sekante, ki se štejejo za sovpadajoče, kar pomeni, da so nastavljene z podobna enačba.

Po definiciji je jasno, da sta premica in njen sekant v v tem primeru ujemati se.

Sekans lahko večkrat seka graf dane funkcije. Če za sekanto obstaja enačba v obliki y = 0, potem je število presečišč s sinusoido neskončno.

Definicija 5

Tangenta na graf funkcije f (x) v točki x 0 ; f (x 0) je premica, ki poteka skozi dano točko x 0; f (x 0), s prisotnostjo segmenta, ki ima veliko vrednosti x blizu x 0.

Primer 1

Oglejmo si spodnji primer podrobneje. Potem je jasno, da se premica, definirana s funkcijo y = x + 1, obravnava kot tangenta na y = 2 x v točki s koordinatami (1; 2). Zaradi jasnosti je treba upoštevati grafe z vrednostmi blizu (1; 2). Funkcija y = 2 x je prikazana s črno, modra črta je tangenta, rdeča pika pa je presečišče.

Očitno se y = 2 x združi s premico y = x + 1.

Za določitev tangente bi morali upoštevati obnašanje tangente A B, ko se točka B neskončno približuje točki A. Zaradi jasnosti predstavljamo risbo.

Sekanta A B, označena z modro črto, teži k položaju same tangente, naklonski kot sekante α pa se bo začel nagibati k naklonskemu kotu same tangente α x.

Opredelitev 6

Tangenta na graf funkcije y = f (x) v točki A velja za mejni položaj sekante A B, ko B teži k A, to je B → A.

Zdaj pa preidimo na geometrični pomen odvoda funkcije v točki.

Preidimo k obravnavanju sekante A B za funkcijo f (x), kjer sta A in B s koordinatami x 0, f (x 0) in x 0 + ∆ x, f (x 0 + ∆ x) in ∆ x je označeno kot prirastek argumenta. Zdaj bo funkcija prevzela obliko ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . Za jasnost navedimo primer risbe.

Upoštevajte nastali pravokotni trikotnik A B C. Za rešitev uporabimo definicijo tangente, to pomeni, da dobimo relacijo ∆ y ∆ x = t g α . Iz definicije tangente sledi lim ∆ x → 0 ∆ y ∆ x = t g α x . Po pravilu odvoda v točki imamo, da se odvod f (x) v točki x 0 imenuje meja razmerja prirastka funkcije in prirastka argumenta, kjer je ∆ x → 0 , potem ga označimo kot f (x 0) = lim ∆ x → 0 ∆ y ∆ x .

Iz tega sledi, da je f " (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, kjer je k x označen kot naklon tangente.

To pomeni, da lahko f ' (x) obstaja v točki x 0 in kot tangenta na dani graf funkcije v točki dotikanja je enaka x 0, f 0 (x 0), kjer je vrednost naklon tangente v točki je enak odvodu v točki x 0 . Potem dobimo, da k x = f " (x 0) .

Geometrijski pomen odvod funkcije v točki je, da je podan koncept obstoja tangente na graf v isti točki.

Za pisanje enačbe katere koli ravne črte na ravnini je potrebno imeti kotni koeficient s točko, skozi katero poteka. Njegov zapis je x 0 na presečišču.

Tangentna enačba na graf funkcije y = f (x) v točki x 0, f 0 (x 0) ima obliko y = f "(x 0) x - x 0 + f (x 0).

To pomeni, da lahko končna vrednost odvoda f "(x 0) določi položaj tangente, to je navpično, če je lim x → x 0 + 0 f "(x) = ∞ in lim x → x 0 - 0 f "(x ) = ∞ ali sploh odsotnost pod pogojem lim x → x 0 + 0 f " (x) ≠ lim x → x 0 - 0 f " (x) .

Lokacija tangente je odvisna od vrednosti njenega kotnega koeficienta k x = f "(x 0). Ko je vzporedna z osjo o x, dobimo, da je k k = 0, ko je vzporedna z o y - k x = ∞, in oblika tangente tangentna enačba x = x 0 narašča s k x > 0, pada kot k x< 0 .

Primer 2

Sestavite enačbo za tangento na graf funkcije y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 v točki s koordinatami (1; 3) in določite naklonski kot.

rešitev

Po pogoju imamo, da je funkcija definirana za vse realna števila. Ugotovimo, da je točka s koordinatami, določenimi s pogojem, (1; 3) dotikalna točka, potem je x 0 = - 1, f (x 0) = - 3.

Treba je najti izpeljanko v točki z vrednostjo - 1. To razumemo

y " = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = e x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = e x + 1 + x 2 - 6 - 3 3 y " (x 0) = y " (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3

Vrednost f' (x) v točki tangente je naklon tangente, ki je enak tangenti naklona.

Potem je k x = t g α x = y " (x 0) = 3 3

Iz tega sledi, da je α x = a r c t g 3 3 = π 6

odgovor: tangentna enačba dobi obliko

y = f " (x 0) x - x 0 + f (x 0) y = 3 3 (x + 1) - 3 y = 3 3 x - 9 - 3 3

Zaradi jasnosti podajamo primer v grafični ilustraciji.

Črna barva je uporabljena za graf izvirne funkcije, Modra barva– slika tangente, rdeča pika – točka dotika. Slika na desni prikazuje povečan pogled.

Primer 3

Ugotovite obstoj tangente na graf dane funkcije
y = 3 · x - 1 5 + 1 v točki s koordinatami (1 ; 1) . Napišite enačbo in določite naklonski kot.

rešitev

Po pogoju imamo, da je domena definicije dane funkcije množica vseh realnih števil.

Pojdimo k iskanju izpeljanke

y " = 3 x - 1 5 + 1 " = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5

Če je x 0 = 1, potem je f' (x) nedefiniran, vendar so limite zapisane kot lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 · 1 + 0 = + ∞ in lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , kar pomeni, da obstojna navpična tangenta v točki (1; 1).

odgovor: enačba bo imela obliko x = 1, kjer bo naklonski kot enak π 2.

Za večjo jasnost ga predstavimo grafično.

Primer 4

Poiščite točke na grafu funkcije y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2, kjer je

1. Ni tangente;
2. Tangenta je vzporedna z x;
3. Tangenta je vzporedna s premico y = 8 5 x + 4.

rešitev

Treba je paziti na obseg definicije. Po pogoju velja, da je funkcija definirana na množici vseh realnih števil. Modul razširimo in rešimo sistem z intervali x ∈ - ∞ ; 2 in [-2; + ∞). To razumemo

y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; + ∞)

Treba je razlikovati funkcijo. To imamo

y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 ", x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; + ∞)

Ko je x = − 2, potem odvod ne obstaja, ker enostranski limiti na tej točki niso enaki:

lim x → - 2 - 0 y " (x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y " (x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

Vrednost funkcije izračunamo v točki x = - 2, kjer to dobimo

1. y (- 2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2, to je tangenta v točki ( - 2; - 2) ne bo obstajalo.
2. Tangenta je vzporedna z x, ko je naklon enak nič. Potem k x = t g α x = f "(x 0). To pomeni, da je treba najti vrednosti takega x, ko ga derivat funkcije spremeni v nič. To je vrednosti f ' (x) bodo dotične točke, kjer je tangenta vzporedna z x.

Ko je x ∈ - ∞ ; - 2, potem - 1 5 (x 2 + 12 x + 35) = 0, za x ∈ (- 2; + ∞) pa dobimo 1 5 (x 2 - 4 x + 3) = 0.

1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞

Izračunaj ustrezne vrednosti funkcij

y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3

Torej - 5; 8 5, - 4; 4 3, 1; 8 5, 3; 4 3 veljajo za zahtevane točke funkcijskega grafa.

Poglejmo si grafični prikaz rešitve.

Črna črta je graf funkcije, rdeče pike pa so dotične točke.

1. Ko sta premici vzporedni, sta kotna koeficienta enaka. Nato je treba na grafu funkcije poiskati točke, kjer bo naklon enak vrednosti 8 5. Če želite to narediti, morate rešiti enačbo v obliki y "(x) = 8 5. Potem, če je x ∈ - ∞; - 2, dobimo, da je - 1 5 (x 2 + 12 x + 35) = 8 5, in če je x ∈ ( - 2 ; + ∞), potem je 1 5 (x 2 - 4 x + 3) = 8 5.

Prva enačba nima korenin, ker je diskriminant manjši od nič. Zapišimo to

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0

Druga enačba ima torej dva realna korena

1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞

Pojdimo k iskanju vrednosti funkcije. To razumemo

y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3

Točke z vrednostmi - 1; 4 15, 5; 8 3 so točke, v katerih so tangente vzporedne s premico y = 8 5 x + 4.

odgovor:črna črta – graf funkcije, rdeča črta – graf od y = 8 5 x + 4, modra črta – tangente v točkah - 1; 4 15, 5; 8 3.

Za dane funkcije je lahko neskončno število tangent.

Primer 5

Zapišite enačbe vseh razpoložljivih tangent funkcij y = 3 cos 3 2 x - π 4 - 1 3, ki se nahajajo pravokotno na premico y = - 2 x + 1 2.

rešitev

Za sestavljanje tangentne enačbe je treba najti koeficient in koordinate tangentne točke, ki temelji na pogoju pravokotnosti črt. Definicija je naslednja: produkt kotnih koeficientov, ki so pravokotni na ravne črte, je enak - 1, kar je zapisano kot k x · k ⊥ = - 1. Iz pogoja imamo, da se kotni koeficient nahaja pravokotno na premico in je enak k ⊥ = - 2, potem je k x = - 1 k ⊥ = - 1 - 2 = 1 2.

Zdaj morate najti koordinate točk dotika. Najti morate x in nato njegovo vrednost za dano funkcijo. Upoštevajte, da iz geometrijskega pomena odvoda v točki
x 0 dobimo, da je k x = y "(x 0). Iz te enakosti najdemo vrednosti x za stične točke.

To razumemo

y " (x 0) = 3 cos 3 2 x 0 - π 4 - 1 3 " = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 = - 9 2 sin 3 2 x 0 - π 4 ⇒ k x = y " (x 0) ⇔ - 9 2 sin 3 2 x 0 - π 4 = 1 2 ⇒ sin 3 2 x 0 - π 4 = - 1 9

Ta trigonometrična enačba bo uporabljena za izračun ordinat tangentnih točk.

3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk ali 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk

3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk ali 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk ali x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z je množica celih števil.

Najdenih je bilo x stičnih točk. Zdaj se morate premakniti na iskanje vrednosti y:

y 0 = 3 cos 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - sin 2 3 2 x 0 - π 4 - 1 3 ali y 0 = 3 - 1 - sin 2 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - - 1 9 2 - 1 3 ali y 0 = 3 - 1 - - 1 9 2 - 1 3

y 0 = 4 5 - 1 3 ali y 0 = - 4 5 + 1 3

Iz tega dobimo, da je 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; - 4 5 + 1 3 so dotične točke.

odgovor: potrebne enačbe bodo zapisane kot

y = 1 2 x - 2 3 π 4 - a r c sin 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + a r c sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z

Za vizualno predstavitev razmislite o funkciji in tangenti na koordinatni premici.

Slika prikazuje, da se funkcija nahaja na intervalu [ - 10 ; 10 ], kjer je črna črta graf funkcije, modre črte pa so tangente, ki ležijo pravokotno na dano premico oblike y = - 2 x + 1 2. Rdeče pike so točke dotika.

Kanonične enačbe krivulj 2. reda niso funkcije z eno vrednostjo. Tangentne enačbe zanje so sestavljene po znanih shemah.

Tangenta na krožnico

Za določitev kroga s središčem v točki x c e n t e r ; y cent e r in polmer R, uporabite formulo x - x cent e r 2 + y - y cent e r 2 = R 2 .

To enakost lahko zapišemo kot zvezo dveh funkcij:

y = R 2 - x - x središče 2 + y središče y = - R 2 - x - x središče 2 + y središče

Prva funkcija se nahaja zgoraj, druga pa spodaj, kot je prikazano na sliki.

Sestaviti enačbo kroga v točki x 0; y 0 , ki se nahaja v zgornjem ali spodnjem polkrogu, morate najti enačbo grafa funkcije oblike y = R 2 - x - x c e n t e r 2 + y c e n t e r ali y = - R 2 - x - x c e n t e r 2 + y c e n t e r na označeni točki.

Ko je v točkah x c e n t e r; y cent r + R in x cent e r; y c e n t e r - R tangente lahko podamo z enačbama y = y c e n t e r + R in y = y c e n t e r - R ter v točkah x c e n t e r + R ; y c e n t e r in
x c e n t e r - R; y c e n t e r bo vzporeden z o y, potem dobimo enačbe oblike x = x c e n t e r + R in x = x c e n t e r - R .

Tangenta na elipso

Ko ima elipsa središče v x c e n t e r ; y c e n t e r s polosema a in b, potem ga lahko podamo z enačbo x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1.

Elipso in krog lahko označimo tako, da združimo dve funkciji, in sicer zgornjo in spodnjo polelipso. Potem to razumemo

y = b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r

Če se tangente nahajajo na ogliščih elipse, potem so vzporedne glede na x ali okoli y. Spodaj, zaradi jasnosti, upoštevajte sliko.

Primer 6

Zapišite enačbo tangente na elipso x - 3 2 4 + y - 5 2 25 = 1 v točkah z vrednostmi x, ki so enake x = 2.

rešitev

Treba je najti tangentne točke, ki ustrezajo vrednosti x = 2. Nadomestimo v obstoječo enačbo elipse in ugotovimo, da

x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5

Potem 2; 5 3 2 + 5 in 2; - 5 3 2 + 5 sta tangentni točki, ki pripadata zgornji in spodnji polelipsi.

Pojdimo k iskanju in reševanju enačbe elipse glede na y. To razumemo

x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2

Očitno je zgornja polovična elipsa podana s funkcijo oblike y = 5 + 5 2 4 - x - 3 2, spodnja polovična elipsa pa y = 5 - 5 2 4 - x - 3 2.

Uporabimo standardni algoritem za ustvarjanje enačbe za tangento na graf funkcije v točki. Zapišimo, da enačba za prvo tangento v točki 2; 5 3 2 + 5 bo videti takole

y " = 5 + 5 2 4 - x - 3 2 " = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y " (x 0) = y " (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5

Ugotovimo, da je enačba druge tangente z vrednostjo v točki
2 ; - 5 3 2 + 5 dobi obliko

y " = 5 - 5 2 4 - (x - 3) 2 " = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y " (x 0) = y " (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5

Grafično so tangente označene na naslednji način:

Tangenta na hiperbolo

Ko ima hiperbola središče v x c e n t e r ; y e n t e r in oglišča x e n t e r + α ; y c e n t e r in x c e n t e r - α ; y c e n t e r , velja neenakost x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1, če z oglišči x c e n t e r ; y c e n t e r + b in x c e n t e r ; y c e n t e r - b , potem je podana z uporabo neenačbe x-x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

Hiperbolo lahko predstavimo kot dve kombinirani funkciji oblike

y = b a · (x - x cent) 2 - a 2 + y cent y = - b a · (x - x cent) 2 - a 2 + y cent ali y = b a · (x - x cent) 2 + a 2 + y cent y = - b a · (x - x središče) 2 + a 2 + y središče

V prvem primeru imamo, da sta tangenti vzporedni z y, v drugem pa z x.

Iz tega sledi, da je treba za iskanje enačbe tangente na hiperbolo ugotoviti, kateri funkciji pripada tangentna točka. Da bi to ugotovili, je treba zamenjati v enačbe in preveriti istovetnost.

Primer 7

Zapišite enačbo za tangento na hiperbolo x - 3 2 4 - y + 3 2 9 = 1 v točki 7; - 3 3 - 3 .

rešitev

Potrebno je transformirati zapis rešitve za iskanje hiperbole z uporabo 2 funkcij. To razumemo

x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 in y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3

Ugotoviti je treba, kateri funkciji pripada določena točka s koordinatami 7; - 3 3 - 3 .

Očitno je za preverjanje prve funkcije potrebno y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3, potem točka ne pripada grafu, saj enakost ne velja.

Za drugo funkcijo velja, da je y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3, kar pomeni, da točka pripada danemu grafu. Od tu bi morali najti pobočje.

To razumemo

y " = - 3 2 (x - 3) 2 - 4 - 3 " = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y " (x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3

odgovor: tangentno enačbo lahko predstavimo kot

y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3

Jasno je prikazano takole:

Tangenta na parabolo

Če želite ustvariti enačbo za tangento na parabolo y = a x 2 + b x + c v točki x 0, y (x 0), morate uporabiti standardni algoritem, nato pa bo enačba imela obliko y = y "(x 0) x - x 0 + y ( x 0). Takšna tangenta na oglišču je vzporedna z x.

Parabolo x = a y 2 + b y + c bi morali definirati kot unijo dveh funkcij. Zato moramo rešiti enačbo za y. To razumemo

x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a

Grafično prikazano kot:

Če želite ugotoviti, ali točka x 0, y (x 0) pripada funkciji, nežno nadaljujte po standardnem algoritmu. Takšna tangenta bo vzporedna z o y glede na parabolo.

Primer 8

Zapišite enačbo tangente na graf x - 2 y 2 - 5 y + 3, ko imamo kot tangente 150 °.

rešitev

Rešitev začnemo tako, da parabolo predstavimo kot dve funkciji. To razumemo

2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4

Vrednost naklona je enaka vrednosti odvoda v točki x 0 te funkcije in je enaka tangensu naklonskega kota.

Dobimo:

k x = y "(x 0) = t g α x = t g 150 ° = - 1 3

Od tu določimo vrednost x za stične točke.

Prva funkcija bo zapisana kot

y " = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3

Očitno ni pravih korenin, saj smo dobili negativno vrednost. Sklepamo, da za tako funkcijo ne obstaja tangenta s kotom 150°.

Druga funkcija bo zapisana kot

y " = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4

Imamo, da sta stični točki 23 4 ; - 5 + 3 4 .

odgovor: tangentna enačba dobi obliko

y = - 1 3 x - 23 4 + - 5 + 3 4

Predstavimo grafično takole:

Če v besedilu opazite napako, jo označite in pritisnite Ctrl+Enter

Y = f(x) in če na tej točki lahko na graf funkcije potegnemo tangento, ki ni pravokotna na abscisno os, potem je kotni koeficient tangente enak f"(a). Smo že to večkrat uporabil.V § 33 je bilo na primer ugotovljeno, da tvori graf funkcije y = sin x (sinusoida) v izhodišču kot 45° z osjo x (natančneje s tangento na graf v izhodišču tvori kot 45° s pozitivno smerjo osi x), v primeru 5 § pa je bilo na danem razporedu najdenih 33 točk funkcije, pri katerem je tangenta vzporedna z osjo x. V primeru 2 § 33 je bila sestavljena enačba za tangento na graf funkcije y = x 2 v točki x = 1 (natančneje v točki (1; 1), pogosteje pa je le vrednost abscise indicirano, saj verjamemo, da če je znana vrednost abscise, potem lahko vrednost ordinate najdemo iz enačbe y = f(x)). V tem razdelku bomo razvili algoritem za sestavljanje tangentne enačbe na graf katere koli funkcije.

Naj sta dana funkcija y = f(x) in točka M (a; f(a)), prav tako je znano, da f"(a) obstaja. Sestavimo enačbo za tangento na graf dana funkcija v dano točko. Ta enačba, tako kot enačba katere koli premice, ki ni vzporedna z ordinatno osjo, ima obliko y = kx+m, zato je naloga najti vrednosti koeficientov k in m.

S kotnim koeficientom k ni težav: vemo, da je k = f "(a). Za izračun vrednosti m uporabimo dejstvo, da želena premica poteka skozi točko M(a; f (a)) To pomeni, da če koordinatno točko M nadomestimo v enačbo premice, dobimo pravilno enakost: f(a) = ka+m, iz katere ugotovimo, da je m = f(a) - ka.
Ostaja, da nadomestimo najdene vrednosti koeficientov kompleta enačba naravnost:

Dobili smo enačbo za tangento na graf funkcije y = f(x) v točki x=a.
Če recimo,
Če zamenjamo najdene vrednosti a = 1, f(a) = 1 f"(a) = 2 v enačbo (1), dobimo: y = 1+2(x-f), tj. y = 2x-1.
Primerjaj ta rezultat s tistim v primeru 2 iz § 33. Seveda se je zgodilo isto.
Ustvarimo enačbo za tangento na graf funkcije y = tan x v izhodišču. Imamo: to pomeni cos x f"(0) = 1. Če nadomestimo ugotovljene vrednosti a = 0, f(a) = 0, f"(a) = 1 v enačbo (1), dobimo: y = x.
Zato smo v § 15 (glej sliko 62) narisali tangentoid skozi koordinatno izhodišče pod kotom 45° na abscisno os.
Reševanje teh dovolj preprosti primeri, smo dejansko uporabili določen algoritem, ki je vsebovan v formuli (1). Naredimo ta algoritem ekspliciten.

ALGORITEM ZA RAZVOJ ENAČBE ZA TANGENTO NA GRAF FUNKCIJE y = f(x)

1) Absciso tangente označimo s črko a.
2) Izračunaj 1 (a).
3) Poiščite f"(x) in izračunajte f"(a).
4) Najdena števila a, f(a), (a) zamenjajte v formulo (1).

Primer 1. Zapišite enačbo za tangento na graf funkcije v točki x = 1.
Uporabimo algoritem, pri čemer upoštevamo, da v tem primeru

Na sl. 126 je upodobljena hiperbola, zgrajena je premica y = 2.
Risba potrjuje zgornje izračune: premica y = 2 se res dotika hiperbole v točki (1; 1).

odgovor: y = 2- x.
Primer 2. Na graf funkcije nariši tangento tako, da bo vzporedna s premico y = 4x - 5.
Naj pojasnimo formulacijo problema. Zahteva za "risanje tangente" običajno pomeni "oblikovati enačbo za tangento". To je logično, kajti če je oseba lahko ustvarila enačbo za tangento, potem verjetno ne bo imel težav pri konstruiranju ravne črte na koordinatni ravnini z njeno enačbo.
Uporabimo algoritem za sestavo tangentne enačbe, pri čemer upoštevamo, da je v tem primeru za razliko od prejšnjega primera dvoumnost: abscisa tangentne točke ni izrecno navedena.
Začnimo razmišljati takole. Želena tangenta mora biti vzporedna s premico y = 4x-5. Dve premici sta vzporedni, če in samo če sta njuna naklona enaka. To pomeni, da mora biti kotni koeficient tangente enak kotnemu koeficientu dane premice: Tako lahko vrednost a najdemo iz enačbe f"(a) = 4.
Imamo:
Iz enačbe To pomeni, da obstajata dve tangenti, ki izpolnjujeta pogoje problema: ena v točki z absciso 2, druga v točki z absciso -2.
Zdaj lahko sledite algoritmu.

Primer 3. Iz točke (0; 1) nariši tangento na graf funkcije
Uporabimo algoritem za sestavo tangentne enačbe, pri čemer upoštevamo, da v tem primeru Upoštevajte, da tudi tukaj, tako kot v primeru 2, abscisa tangentne točke ni eksplicitno navedena. Kljub temu sledimo algoritmu.

Po pogoju gre tangenta skozi točko (0; 1). Če nadomestimo vrednosti x = 0, y = 1 v enačbo (2), dobimo:
Kot lahko vidite, nam je v tem primeru šele v četrtem koraku algoritma uspelo najti absciso tangentne točke. Če zamenjamo vrednost a =4 v enačbo (2), dobimo:

Na sl. 127 predstavlja geometrijsko ponazoritev obravnavanega primera: izrisan je graf funkcije

V § 32 smo ugotovili, da za funkcijo y = f(x), ki ima odvod v fiksni točki x, velja približna enakost:

Za udobje nadaljnjega sklepanja spremenimo zapis: namesto x bomo napisali a, namesto x bomo napisali in v skladu s tem namesto x-a. Potem bo zgoraj zapisana približna enakost imela obliko:

Poglejte zdaj sl. 128. Na graf funkcije y = f(x) je v točki M (a; f (a)) narisana tangenta. Točka x je označena na osi x blizu a. Jasno je, da je f(x) ordinata grafa funkcije v določeni točki x. Kaj je f(a) + f"(a) (x-a)? To je ordinata tangente, ki ustreza isti točki x - glej formulo (1). Kaj pomeni približna enakost (3)? Dejstvo da Za izračun približne vrednosti funkcije vzemite ordinatno vrednost tangente.

Primer 4. Poiščite približno vrednost številski izraz 1,02 7 .
To je približno o iskanju vrednosti funkcije y = x 7 v točki x = 1,02. Uporabimo formulo (3), pri čemer upoštevamo, da v tem primeru
Kot rezultat dobimo:

Če uporabimo kalkulator, dobimo: 1,02 7 = 1,148685667...
Kot lahko vidite, je natančnost približka povsem sprejemljiva.
odgovor: 1,02 7 =1,14.

A.G. Mordkovič algebra 10. razred

Koledarsko-tematsko načrtovanje pri matematiki, video pri matematiki na spletu, Matematika v šoli download

Vsebina lekcije zapiski lekcije podporni okvir predstavitev lekcije metode pospeševanja interaktivne tehnologije Vadite naloge in vaje samotestiranje delavnice, treningi, primeri, questi domače naloge diskusija vprašanja retorična vprašanja študentov Ilustracije avdio, video posnetki in multimedija fotografije, slike, grafike, tabele, diagrami, humor, anekdote, šale, stripi, prispodobe, izreki, križanke, citati Dodatki izvlečkičlanki triki za radovedneže jaslice učbeniki osnovni in dodatni slovar pojmov drugo Izboljšanje učbenikov in poukapopravljanje napak v učbeniku posodobitev odlomka v učbeniku, elementi inovativnosti pri pouku, nadomeščanje zastarelega znanja z novim Samo za učitelje popolne lekcije koledarski načrt za eno leto smernice diskusijski programi Integrirane lekcije

Enačba tangente na graf funkcije

P. Romanov, T. Romanova,
Magnitogorsk,
Čeljabinska regija

Enačba tangente na graf funkcije

Članek je bil objavljen ob podpori Hotelskega kompleksa ITAKA+. Ko bivate v mestu ladjedelnikov Severodvinsk, ne boste naleteli na težavo iskanja začasnega bivališča. , na spletni strani hotelskega kompleksa “ITHAKA+” http://itakaplus.ru, lahko enostavno in hitro najamete stanovanje v mestu, za katero koli obdobje, z dnevnim plačilom.

Vklopljeno moderni oder razvoj izobraževanja, je ena njegovih glavnih nalog oblikovanje ustvarjalno misleče osebnosti. Sposobnost za ustvarjalnost pri študentih je mogoče razviti le, če se sistematično ukvarjajo z osnovami raziskovalne dejavnosti. Osnova, da učenci uporabljajo svoje ustvarjalne moči, sposobnosti in talente, so oblikovana polnovredna znanja in spretnosti. V zvezi s tem je problem oblikovanja sistema osnovnih znanj in spretnosti za vsako temo šolskega tečaja matematike nepomemben. Hkrati bi morale biti popolne spretnosti didaktični cilj ne posameznih nalog, temveč njihovega skrbno premišljenega sistema. V najširšem smislu sistem razumemo kot niz medsebojno povezanih elementov, ki delujejo celovito in imajo stabilno strukturo.

Oglejmo si tehniko za učenje študentov, kako napisati enačbo za tangento na graf funkcije. V bistvu se vsi problemi pri iskanju tangentne enačbe zmanjšajo na to, da je treba iz nabora (svežnja, družine) črt izbrati tiste, ki izpolnjujejo določeno zahtevo - se dotikajo grafa določene funkcije. V tem primeru je nabor vrstic, iz katerih se izvaja izbor, mogoče določiti na dva načina:

a) točka, ki leži na ravnini xOy (osrednji svinčnik premic);
b) kotni koeficient (vzporedni žarek ravnih črt).

V zvezi s tem smo pri preučevanju teme "Tangenta na graf funkcije", da bi izolirali elemente sistema, identificirali dve vrsti težav:

1) težave s tangento, ki jo določa točka, skozi katero poteka;
2) težave na tangenti, ki jo določa njen naklon.

Usposabljanje reševanja tangentnih problemov je potekalo z uporabo algoritma, ki ga je predlagal A.G. Mordkovič. Njegovo temeljna razlika od že znanih je, da je abscisa tangentne točke označena s črko a (namesto z x0), zato ima enačba tangente obliko

y = f(a) + f "(a)(x – a)

(primerjaj z y = f(x 0) + f "(x 0)(x – x 0)). Ta metodološka tehnika po našem mnenju študentom omogoča hitro in enostavno razumevanje, kje so zapisane koordinate trenutne točke. splošno tangentno enačbo in kje so stične točke.

Algoritem za sestavljanje tangentne enačbe na graf funkcije y = f(x)

1. Absciso tangentne točke označimo s črko a.
2. Poiščite f(a).
3. Poiščite f "(x) in f "(a).
4. Najdene številke a, f(a), f "(a) zamenjajte v splošno tangentno enačbo y = f(a) = f "(a)(x – a).

Ta algoritem je mogoče sestaviti na podlagi študentovega neodvisnega prepoznavanja operacij in zaporedja njihovega izvajanja.

Praksa je pokazala, da vam zaporedna rešitev vsakega od ključnih problemov z uporabo algoritma omogoča razvoj spretnosti pisanja enačbe tangente na graf funkcije v stopnjah, koraki algoritma pa služijo kot referenčne točke za dejanja. . Ta pristop ustreza teoriji postopnega oblikovanja miselnih dejanj, ki jo je razvil P.Ya. Galperin in N.F. Talyzina.

Pri prvem tipu nalog sta bili identificirani dve ključni nalogi:

• tangenta poteka skozi točko, ki leži na krivulji (problem 1);
• tangenta poteka skozi točko, ki ne leži na krivulji (problem 2).

Naloga 1. Zapišite enačbo za tangento na graf funkcije v točki M(3; – 2).

rešitev. Točka M(3; – 2) je tangentna točka, saj

1. a = 3 – abscisa tangentne točke.
2. f(3) = – 2.
3. f "(x) = x 2 – 4, f "(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – tangentna enačba.

Naloga 2. Zapišite enačbe vseh tangent na graf funkcije y = – x 2 – 4x + 2, ki potekajo skozi točko M(– 3; 6).

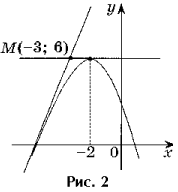rešitev. Točka M(– 3; 6) ni tangentna točka, ker f(– 3) 6 (slika 2).

2. f(a) = – a 2 – 4a + 2.
3. f "(x) = – 2x – 4, f "(a) = – 2a – 4.
4. y = – a 2 – 4a + 2 – 2(a + 2)(x – a) – tangentna enačba.

Tangenta poteka skozi točko M(– 3; 6), zato njene koordinate zadoščajo enačbi tangente.

6 = – a 2 – 4a + 2 – 2(a + 2)(– 3 – a),
a 2 + 6a + 8 = 0^ a 1 = – 4, a 2 = – 2.

Če je a = – 4, je enačba tangente y = 4x + 18.

Če je a = – 2, ima tangentna enačba obliko y = 6.

Pri drugi vrsti bodo ključne naloge naslednje:

• tangenta je vzporedna z neko premico (problem 3);
• tangenta poteka pod določenim kotom na dano premico (naloga 4).

Naloga 3. Zapišite enačbe vseh tangent na graf funkcije y = x 3 – 3x 2 + 3, vzporedne s premico y = 9x + 1.

rešitev.

1. a – abscisa tangentne točke.
2. f(a) = a 3 – 3a 2 + 3.
3. f "(x) = 3x 2 – 6x, f "(a) = 3a 2 – 6a.

Po drugi strani pa je f "(a) = 9 (pogoj vzporednosti). To pomeni, da moramo rešiti enačbo 3a 2 – 6a = 9. Njene korenine so a = – 1, a = 3 (slika 3 ).

4. 1) a = – 1;
2) f(– 1) = – 1;
3) f "(– 1) = 9;
4) y = – 1 + 9(x + 1);

y = 9x + 8 – tangentna enačba;

1) a = 3;
2) f(3) = 3;
3) f "(3) = 9;
4) y = 3 + 9(x – 3);

y = 9x – 24 – tangentna enačba.

Naloga 4. Zapišite enačbo tangente na graf funkcije y = 0,5x 2 – 3x + 1, ki poteka pod kotom 45° na premico y = 0 (slika 4).

rešitev. Iz pogoja f "(a) = tan 45° dobimo a: a – 3 = 1^a = 4.

1. a = 4 – abscisa tangentne točke.
2. f(4) = 8 – 12 + 1 = – 3.
3. f "(4) = 4 – 3 = 1.
4. y = – 3 + 1 (x – 4).

y = x – 7 – tangentna enačba.

Zlahka je pokazati, da se rešitev katerega koli drugega problema zmanjša na rešitev enega ali več ključnih problemov. Razmislite o naslednjih dveh težavah kot primeru.

1. Zapišite enačbe tangent na parabolo y = 2x 2 – 5x – 2, če se tangenti sekata pod pravim kotom in se ena od njiju dotika parabole v točki z absciso 3 (slika 5).

rešitev. Ker je abscisa tangente podana, se prvi del rešitve skrči na ključni problem 1.

1. a = 3 – abscisa dotične točke ene od stranic pravega kota.
2. f(3) = 1.
3. f "(x) = 4x – 5, f "(3) = 7.
4. y = 1 + 7(x – 3), y = 7x – 20 – enačba prve tangente.

Naj a – kot naklona prve tangente. Ker sta tangenti pravokotni, je naklonski kot druge tangente. Iz enačbe y = 7x – 20 prve tangente imamo tg a = 7. Poiščimo

To pomeni, da je naklon druge tangente enak .

Nadaljnja rešitev se skrči na ključno nalogo 3.

Naj bo B(c; f(c)) točka dotika druge premice

1. – abscisa druge dotične točke.
2.
3.
4.
– enačba druge tangente.

Opomba. Kotni koeficient tangente je lažje najti, če učenci poznajo razmerje koeficientov pravokotnic k 1 k 2 = – 1.

2. Zapišite enačbe vseh skupnih tangent na grafe funkcij

rešitev. Naloga se zmanjša na iskanje abscis tangentnih točk skupnih tangent, to je rešitev ključnega problema 1 v splošni obliki, sestavljanje sistema enačb in njegovo reševanje (slika 6).

1. Naj bo a abscisa tangente, ki leži na grafu funkcije y = x 2 + x + 1.
2. f(a) = a 2 + a + 1.
3. f "(a) = 2a + 1.
4. y = a 2 + a + 1 + (2a + 1)(x – a) = (2a + 1)x + 1 – a 2 .

1. Naj bo c abscisa tangente, ki leži na grafu funkcije
2.
3. f "(c) = c.
4.

Ker so tangente splošne, torej

Torej sta y = x + 1 in y = – 3x – 3 skupni tangenti.

Glavni cilj obravnavanih nalog je pripraviti študente na samostojno prepoznavanje vrste ključnega problema pri reševanju kompleksnejših problemov, ki zahtevajo določene raziskovalne sposobnosti (sposobnost analiziranja, primerjanja, posploševanja, postavljanja hipotez ipd.). Takšne naloge vključujejo vse naloge, v katere je ključna naloga vključena kot komponenta. Vzemimo za primer problem (obraten problemu 1) iskanja funkcije iz družine njenih tangent.

3. Za koliko b in c se premici y = x in y = – 2x dotikata grafa funkcije y = x 2 + bx + c?

rešitev.

Naj bo t abscisa dotične točke premice y = x s parabolo y = x 2 + bx + c; p je abscisa dotične točke premice y = – 2x s parabolo y = x 2 + bx + c. Takrat bo tangentna enačba y = x imela obliko y = (2t + b)x + c – t 2 , tangentna enačba y = – 2x pa bo imela obliko y = (2p + b)x + c – p 2 .

Sestavimo in rešimo sistem enačb

odgovor:

Težave, ki jih je treba rešiti neodvisno

1. Zapišite enačbe tangent, narisanih na graf funkcije y = 2x 2 – 4x + 3 v presečiščih grafa s premico y = x + 3.

Odgovor: y = – 4x + 3, y = 6x – 9,5.

2. Za katere vrednosti a gre tangenta, narisana na graf funkcije y = x 2 – ax v točki grafa z absciso x 0 = 1, skozi točko M(2; 3)?

Odgovor: a = 0,5.

3. Pri katerih vrednostih p se premica y = px – 5 dotika krivulje y = 3x 2 – 4x – 2?

Odgovor: p 1 = – 10, p 2 = 2.

4. Poiščite vse skupne točke grafa funkcije y = 3x – x 3 in tangente, ki poteka na ta graf skozi točko P(0; 16).

Odgovor: A(2; – 2), B(– 4; 52).

5. Poiščite najkrajšo razdaljo med parabolo y = x 2 + 6x + 10 in premico

odgovor:

6. Na krivulji y = x 2 – x + 1 poiščite točko, v kateri je tangenta na graf vzporedna s premico y – 3x + 1 = 0.

Odgovor: M(2; 3).

7. Zapišite enačbo tangente na graf funkcije y = x 2 + 2x – | 4x |, ki se ga dotika v dveh točkah. Narišite risbo.

Odgovor: y = 2x – 4.

8. Dokaži, da premica y = 2x – 1 ne seka krivulje y = x 4 + 3x 2 + 2x. Poiščite razdaljo med njunima najbližjima točkama.

odgovor:

9. Na paraboli y = x 2 sta vzeti dve točki z abscisama x 1 = 1, x 2 = 3. Skozi ti točki narišemo sekanto. Na kateri točki parabole bo tangenta nanjo vzporedna s sekanto? Napiši enačbo sekante in tangente.

Odgovor: y = 4x – 3 – enačba sekante; y = 4x – 4 – tangentna enačba.

10. Poiščite kot q med tangentama na graf funkcije y = x 3 – 4x 2 + 3x + 1, narisan v točkah z abscisama 0 in 1.

Odgovor: q = 45°.

11. V katerih točkah oklepa tangenta na graf funkcije z osjo Ox kot 135°?

Odgovor: A(0; – 1), B(4; 3).

12. V točki A(1; 8) do krivulje narisana je tangenta. Poiščite dolžino tangentnega odseka med koordinatnima osema.

odgovor:

13. Na grafa funkcij y = x 2 – x + 1 in y = 2x 2 – x + 0,5 zapišite enačbo vseh skupnih tangent.

Odgovor: y = – 3x in y = x.

14. Poiščite razdaljo med tangentama na graf funkcije vzporedno z osjo x.

odgovor:

15. Ugotovite, pod kakšnimi koti parabola y = x 2 + 2x – 8 seka os x.

Odgovor: q 1 = arctan 6, q 2 = arctan (– 6).

16. Funkcijski graf poiščite vse točke, od katerih tangenta na ta graf seka pozitivne pol-osi koordinat in od njih odreže enake segmente.

Odgovor: A(– 3; 11).

17. Premica y = 2x + 7 in parabola y = x 2 – 1 se sekata v točkah M in N. Poiščite točko K presečišča premic, ki se dotikajo parabole v točkah M in N.

Odgovor: K(1; – 9).

18. Za katere vrednosti b je premica y = 9x + b tangentna na graf funkcije y = x 3 – 3x + 15?

Odgovor: – 1; 31.

19. Za katere vrednosti k ima ravna črta y = kx – 10 samo eno skupna točka z grafom funkcije y = 2x 2 + 3x – 2? Za najdene vrednosti k določite koordinate točke.

Odgovor: k 1 = – 5, A(– 2; 0); k 2 = 11, B(2; 12).

20. Pri katerih vrednostih b gre tangenta, narisana na graf funkcije y = bx 3 – 2x 2 – 4 v točki z absciso x 0 = 2, skozi točko M(1; 8)?

Odgovor: b = – 3.

21. Parabola z vrhom na osi Ox se v točki B dotika premice, ki poteka skozi točki A(1; 2) in B(2; 4). Poiščite enačbo parabole.

odgovor:

22. Pri kateri vrednosti koeficienta k se parabola y = x 2 + kx + 1 dotika osi Ox?

Odgovor: k = d 2.

23. Poiščite kote med premico y = x + 2 in krivuljo y = 2x 2 + 4x – 3.

29. Poiščite razdaljo med tangentama na graf funkcije in generatorje s pozitivno smerjo osi Ox pod kotom 45°.

odgovor:

30. Poiščite geometrijsko mesto oglišč vseh parabol oblike y = x 2 + ax + b, ki se dotikajo premice y = 4x – 1.

Odgovor: premica y = 4x + 3.

Literatura

1. Zvavič L.I., Shlyapochnik L.Ya., Chinkina M.V. Algebra in začetki analize: 3600 nalog za šolarje in vpisnike. – M., Bustard, 1999.
2. Mordkovich A. Seminar štiri za mlade učitelje. Tema: Izpeljane aplikacije. – M., “Matematika”, št. 21/94.
3. Oblikovanje znanja in spretnosti na podlagi teorije postopnega usvajanja miselnih dejanj. / Ed. P.Ya. Galperina, N.F. Talyzina. – M., Moskovska državna univerza, 1968.

V tem članku bomo analizirali vse vrste težav, ki jih je treba najti

Spomnimo se geometrijski pomen izpeljanke: če na graf funkcije v točki narišemo tangento, potem je koeficient naklona tangente (enak tangensu kota med tangento in pozitivno smerjo osi) enak odvodu funkcije na točki.

Vzemimo poljubno točko na tangenti s koordinatami:

In razmislite o pravokotnem trikotniku:

V tem trikotniku

Od tod

To je enačba tangente, narisane na graf funkcije v točki.

Za pisanje enačbe tangente moramo poznati le enačbo funkcije in točko, v kateri je tangenta narisana. Potem lahko najdemo in.

Obstajajo tri glavne vrste problemov tangentne enačbe.

1. Glede na kontaktno točko

2. Podan je koeficient nagiba tangente, to je vrednost odvoda funkcije v točki.

3. Dane so koordinate točke, skozi katero poteka tangenta, ki pa ni tangentna točka.

Oglejmo si vsako vrsto naloge.

1. Napišite enačbo tangente na graf funkcije na točki .

.

b) Poiščite vrednost odvoda v točki . Najprej poiščimo odvod funkcije

Zamenjajmo najdene vrednosti v tangentno enačbo:

Odprimo oklepaje na desni strani enačbe. Dobimo:

odgovor: .

2. Poiščite absciso točk, v katerih se funkcije dotikajo grafa vzporedno z osjo x.

Če je tangenta vzporedna z osjo x, je torej kot med tangento in pozitivno smerjo osi enak nič, zato je tangens kota tangente enak nič. To pomeni, da je vrednost odvoda funkcije na stičnih točkah je nič.

a) Poiščite odvod funkcije .

b) Izenačimo odvod na nič in poiščemo vrednosti, v katerih je tangenta vzporedna z osjo:

Če vsak faktor enačimo z nič, dobimo:

Odgovor: 0;3;5

3. Napišite enačbe za tangente na graf funkcije , vzporedno naravnost .

Tangenta je vzporedna s premico. Naklon te premice je -1. Ker je tangenta vzporedna s to premico, je torej tudi naklon tangente -1. To je poznamo naklon tangente, in s tem, vrednost izpeljanke v točki dotika.

To je druga vrsta problema za iskanje tangentne enačbe.

Torej imamo funkcijo in vrednost odvoda v točki dotika.

a) Poiščite točke, v katerih je odvod funkcije enak –1.

Najprej poiščimo izpeljano enačbo.

Izenačimo odvod s številom -1.

Poiščimo vrednost funkcije v točki.

(pogojno)

.

b) Poiščite enačbo tangente na graf funkcije v točki .

Poiščimo vrednost funkcije v točki.

(pogojno).

Zamenjajmo te vrednosti v tangentno enačbo:

.

odgovor:

4. Zapišite enačbo tangente na krivuljo , ki poteka skozi točko

Najprej preverimo, ali je točka tangentna točka. Če je točka tangentna točka, potem pripada grafu funkcije, njene koordinate pa morajo zadoščati enačbi funkcije. Nadomestimo koordinate točke v enačbo funkcije.

Title="1sqrt(8-3^2)">. Мы получили под корнем !} negativno število, enakost ne velja in točka ne pripada grafu funkcije in ni kontaktna točka.

To je zadnja vrsta problema za iskanje tangentne enačbe. Prva stvar najti moramo absciso tangentne točke.

Poiščimo vrednost.

Naj bo kontaktna točka. Točka pripada tangenti na graf funkcije. Če koordinate te točke nadomestimo v enačbo tangente, dobimo pravilno enakost:

.

Vrednost funkcije v točki je .

Poiščimo vrednost odvoda funkcije v točki.

Najprej poiščimo odvod funkcije. ta .

Odvod v točki je enak .

Zamenjajmo izraza za in v enačbo tangente. Dobimo enačbo za:

Rešimo to enačbo.

Zmanjšajte števec in imenovalec ulomka za 2:

Dajmo desna stran enačbe za skupni imenovalec. Dobimo:

Poenostavimo števec ulomka in obe strani pomnožimo z – ta izraz je strogo večji od nič.

Dobimo enačbo

Rešimo to. Če želite to narediti, kvadriramo oba dela in nadaljujemo s sistemom.

Title="delim(lbrace)(matrix(2)(1)((64-48(x_0)+9(x_0)^2=8-(x_0)^2) (8-3x_0>=0 )))( )">!}

Rešimo prvo enačbo.

Odločimo se kvadratna enačba, dobimo

Drugi koren ne izpolnjuje pogoja title="8-3x_0>=0">, следовательно, у нас только одна точка касания и её абсцисса равна .!}

Zapišimo enačbo tangente na krivuljo v točki. Če želite to narediti, zamenjajte vrednost v enačbo - Posneli smo ga že.

odgovor:
.

Tangenta je ravna črta , ki se dotika grafa funkcije v eni točki in katere vse točke so od grafa funkcije najmanj oddaljene. Zato tangenta prehaja tangentno na graf funkcije pod določenim kotom in več tangent pod različnimi koti ne more potekati skozi točko dotika. Tangentne enačbe in normalne enačbe na graf funkcije so sestavljene z uporabo odvoda.

Tangentna enačba izhaja iz enačbe premice .

Izpeljimo enačbo tangente, nato pa še enačbo normale na graf funkcije.

l = kx + b .

V njem k- kotni koeficient.

Od tu dobimo naslednji vnos:

l - l 0 = k(x - x 0 ) .

Izpeljana vrednost f "(x 0 ) funkcije l = f(x) na točki x0 enaka naklonu k= tg φ tangenta na graf funkcije, narisan skozi točko M0 (x 0 , l 0 ) , Kje l0 = f(x 0 ) . To je geometrijski pomen izpeljanke .

Tako lahko zamenjamo k na f "(x 0 ) in dobite naslednje enačba tangente na graf funkcije :

l - l 0 = f "(x 0 )(x - x 0 ) .

Pri težavah, ki vključujejo sestavljanje enačbe tangente na graf funkcije (in nanje bomo kmalu prešli), je treba enačbo, dobljeno iz zgornje formule, zmanjšati na enačba premice v splošni obliki. Če želite to narediti, morate vse črke in številke prenesti na leva stran enačbo in pustite ničlo na desni strani.

Zdaj o normalni enačbi. normalno - to je ravna črta, ki poteka skozi točko dotika na graf funkcije, pravokotno na tangento. Normalna enačba :

(x - x 0 ) + f "(x 0 )(l - l 0 ) = 0

Za ogrevanje vas prosimo, da sami rešite prvi primer in nato pogledate rešitev. Z vsemi razlogi lahko upamo, da ta naloga za naše bralce ne bo "hladen tuš".

Primer 0. Sestavite tangentno enačbo in normalno enačbo za graf funkcije v točki M (1, 1) .

Primer 1. Napišite enačbo tangente in enačbo normale za graf funkcije , če je abscisa tangenta .

Poiščimo odvod funkcije:

Zdaj imamo vse, kar je treba nadomestiti z vnosom v teoretični pomoči, da dobimo enačbo tangente. Dobimo

V tem primeru smo imeli srečo: izkazalo se je, da je naklon enak nič, zato enačbo posebej zmanjšamo na Splošni videz ni bilo potrebno. Zdaj lahko ustvarimo normalno enačbo:

Na spodnji sliki: graf funkcije bordo barva, tangenta Zelena barva, oranžna normalna.

Naslednji primer prav tako ni zapleten: funkcija je, tako kot v prejšnjem, tudi polinom, vendar naklon ne bo enak nič, zato bo dodan še en korak - enačba se spravi v splošno obliko.

Primer 2.

rešitev. Poiščimo ordinato tangentne točke:

Poiščimo odvod funkcije:

.

Poiščimo vrednost odvoda v točki tangente, to je naklon tangente:

Vse dobljene podatke nadomestimo v "prazno formulo" in dobimo tangentno enačbo:

Enačbo spravimo v splošno obliko (na levi strani zberemo vse črke in številke, razen nič, na desni pa pustimo nič):

Sestavimo normalno enačbo:

Primer 3. Zapišite enačbo tangente in enačbo normale na graf funkcije, če je abscisa točka dotika.

rešitev. Poiščimo ordinato tangentne točke:

Poiščimo odvod funkcije:

.

Poiščimo vrednost odvoda v točki tangente, to je naklon tangente:

.

Najdemo tangentno enačbo:

Preden enačbo spravite v splošno obliko, jo morate malo "prečesati": člen za členom pomnožite s 4. To naredimo in enačbo spravimo v splošno obliko:

Sestavimo normalno enačbo:

Primer 4. Zapišite enačbo tangente in enačbo normale na graf funkcije, če je abscisa točka dotika.

rešitev. Poiščimo ordinato tangentne točke:

.

Poiščimo odvod funkcije:

Poiščimo vrednost odvoda v točki tangente, to je naklon tangente:

.

Dobimo tangentno enačbo:

Enačbo pripeljemo do splošne oblike:

Sestavimo normalno enačbo:

Pogosta napaka pri pisanju tangentnih in normalnih enačb je, da ne opazimo, da je funkcija, podana v primeru, kompleksna, in izračunamo njen odvod kot odvod preproste funkcije. Naslednji primeri so že iz kompleksne funkcije(ustrezna lekcija se odpre v novem oknu).

Primer 5. Zapišite enačbo tangente in enačbo normale na graf funkcije, če je abscisa točka dotika.

rešitev. Poiščimo ordinato tangentne točke:

Pozor! Ta funkcija- zapleteno, saj argument tangente (2 x) je sama funkcija. Zato najdemo odvod funkcije kot odvod kompleksne funkcije.